RedisGraph的图存储模型
1 overview
在RedisGraph的整体架构中,非常简略的概括了RedisGraph的图存储模型:
- RedisGraph使用DataBlock来存储node和edge的属性。
- RedisGraph使用稀疏矩阵来表示图,稀疏矩阵的存储格式为按行压缩的稀疏矩阵(Compressed Sparse Row Matrix, CSR_Matrix)。
DataBlock是如何存储node和edge的属性的?使用稀疏矩阵表示图的具体设计有哪些?本文关注RedisGraph的图存储模型。
2 Graph
RedisGraph中的Graph数据结构定义如下:
struct Graph {
DataBlock *nodes; // graph nodes stored in blocks
DataBlock *edges; // graph edges stored in blocks
RG_Matrix adjacency_matrix; // adjacency matrix, holds all graph connections
RG_Matrix *labels; // label matrices
RG_Matrix node_labels; // mapping of all node IDs to all labels possessed by each node
RG_Matrix *relations; // relation matrices
RG_Matrix _zero_matrix; // zero matrix
pthread_rwlock_t _rwlock; // read-write lock scoped to this specific graph
bool _writelocked; // true if the read-write lock was acquired by a writer
SyncMatrixFunc SynchronizeMatrix; // function pointer to matrix synchronization routine
GraphStatistics stats; // graph related statistics
};
-
RedisGraph中存储一张属性图。
属性图由node、relation和property(属性)组成。relation在图中对应edge,node和edge均存在属性(键值对)。
-
RedisGraph使用DataBlock来存储node和edge的属性。
-
RedisGraph使用RG_Matrix来表示图。
3 DataBlock
DataBlock是一种容器数据结构,用于存储同一类型的item。简单理解,DataBlock是一种数组,可以根据index对Block进行查询,只不过是,这个数组设计比较复杂,需要支持高效率的增删查改以及resize操作。
在RedisGraph中,DataBlock的用途之一是存储node和edge的属性(key-value键值对,比如, name: redis-server, ip: 127.0.0.1)。
3.1 the implement of DataBlock
首先,我们看一下DataBlock这个数据结构的定义:
typedef struct {
uint64_t itemCount; // Number of items stored in datablock.
uint64_t itemCap; // Number of items datablock can hold.
uint64_t blockCap; // Number of items a single block can hold.
uint blockCount; // Number of blocks in datablock.
uint itemSize; // Size of a single item in bytes.
Block **blocks; // Array of blocks.
uint64_t *deletedIdx; // Array of free indicies.
fpDestructor destructor; // Function pointer to a clean-up function of an item.
} DataBlock;
typedef struct Block {
size_t itemSize; // Size of a single item in bytes.
struct Block *next; // Pointer to next block.
unsigned char data[]; // Item array. MUST BE LAST MEMBER OF THE STRUCT!
} Block;
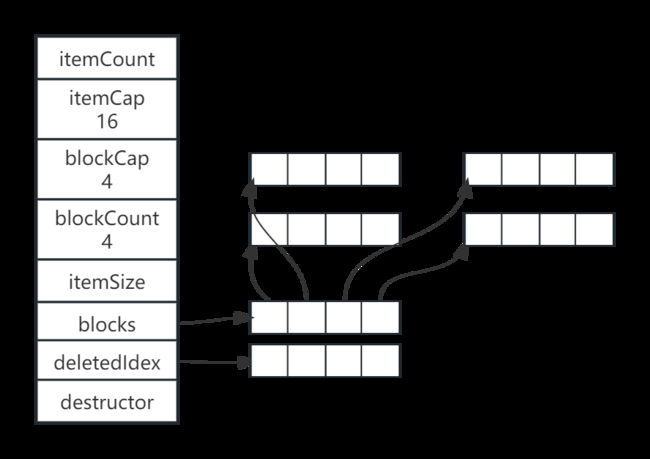
- 一个包含16个item、4个Block的的DataBlock如下图所示:
-
DataBlock要求每一个item的size相同,一般只存储同一种类型的item。
-
每一个item的第一个bit,用于表示item是否被删除,itemSize = sizeof(item)+1。
-
blockCount 表示为block的数量。blockCount = itemCap/blockCap。
-
当DataBlock的容量不足的时候,就会对DataBlock扩容,增加一个Block。此时,会
realloc()blocks数组,将新增的Block指针加到blocks数组末尾。仅支持扩容,不支持缩容。 -
deletedIdx是一个队列,用于暂时存放被释放的item的index。当需要分配新的item的空间时,则优先从deletedIdx取空闲的item的index。
-
Block中存在指向下一个Block的指针。目的是,方便对DataBlock进行遍历操作。
-
查询的时间复杂度为O(1)。
对于查询DataBlock中第idx个item:
Block *block = idx / dataBlock->blockCap; idx = idx % dataBlock->blockCap; void* target_item = block->data + (idx * block->itemSize); -
总的来说,DataBlock是一个增删查改均十分高效的容器数据结构。
3.2 DataBlock for graph store
在RedisGraph中,使用DataBlock存储node和edge的属性。
首先,我们先来看一下Graph_New()中有关创建DataBlock的语句。
#define NODE_CREATION_BUFFER_DEFAULT 16384
Graph *Graph_New
(
size_t node_cap,
size_t edge_cap
) {
.......
g->nodes = DataBlock_New(node_cap, node_cap, sizeof(AttributeSet), cb);
g->edges = DataBlock_New(edge_cap, edge_cap, sizeof(AttributeSet), cb);
.......
}
- 在Graph初始化中,创建了两个DataBlock,分别用于存储node和edge的属性。每个DataBlock中仅含有一个Block。在默认配置下,每一个Block中最多存储16384个item,也就是说,最多存储16384个node或者edge的属性信息。
- 当node和edge数量超过16384时,会触发DataBlock的扩容操作,增加一个Block。
3.3 AttributeSet
在上文中提到了,RedisGraph使用DataBlock存储node和edge的属性。其实,这个说法是不准确的,DataBlock中存储的是指向node和edge属性的指针。毕竟,node和edge的属性(key-value键值对)是不定长的,而指向node和edge属性的指针是定长的。
我们来看一下AttributeSet的定义:
typedef unsigned short Attribute_ID;
typedef struct {
Attribute_ID id; // attribute identifier
SIValue value; // attribute value
} Attribute;
typedef struct {
ushort attr_count; // number of attributes
Attribute attributes[]; // key value pair of attributes
} _AttributeSet;
typedef _AttributeSet* AttributeSet;
- node和edge属性即为key-value键值对,每一个key都对应一个Attribute_ID(unsigned short类型)。
- AttributeSet为执行node和edge属性集合的指针。
- 当向node或edge对应的AttributeSet中添加属性时,首先,_AttributeSet进行重新分配内存空间,然后,再写入相应的属性值。
4 RG_Matrix
RedisGraph使用稀疏矩阵来表示图,稀疏矩阵的存储格式为按行压缩的稀疏矩阵(Compressed Sparse Row Matrix, CSR_Matrix)。实际上,RedisGraph并没有完全自己实现矩阵的存储代码,而是对GraphBLAS中的GrB_Matrix进行了一下封装。
4.1 the implement of RG_Matrix
我们还是先从代码入手,对RG_Matrix进行分析。
struct _RG_Matrix {
bool dirty; // Indicates if matrix requires sync
GrB_Matrix matrix; // Underlying GrB_Matrix
GrB_Matrix delta_plus; // Pending additions
GrB_Matrix delta_minus; // Pending deletions
RG_Matrix transposed; // Transposed matrix
pthread_mutex_t mutex; // Lock
};
typedef struct _RG_Matrix _RG_Matrix;
typedef _RG_Matrix *RG_Matrix;
-
RedisGraph使用GraphBLAS中的GrB_Matrix进行构造RG_Matrix矩阵。RG_Matrix使用了GrB_Matrix的两种存储格式:稀疏矩阵(GxB_SPARSE)和超稀疏矩阵(GxB_HYPERSPARSE)。这两种存储格式将在3.2节中具体介绍。
-
matrix为基础(主)矩阵
-
其存储格式为GxB_SPARSE或GxB_HYPERSPARSE。
-
当matrix中非零元素数量达到一定的阈值时,会由GxB_HYPERSPARSE转变为GxB_SPARSE。
-
-
高效的插入和删除
- delta_plus和delta_minus是插入和删除的缓冲区。
- 对RG_Matrix进行插入元素操作时,被插入元素会被暂存在delta_plus中。
- 当delta_plus中非零元素达到一定阈值时,会批处理(使用矩阵加法算子)写入matrix。matrix=matrix+delta_plus。
- delta_minus同delta_plus,不再赘述。
- delta_plus和delta_minus的存储格式为GxB_HYPERSPARSE。
-
对于一些存储图关系的矩阵,RedisGraph会存储其转置矩阵,方便图查询。
- 当一个搜索模式
(N0)-[A]->(N1)-[B]->(N2)<-[A]-(N3)被用作查询的一部分时,需要使用A的转置矩阵Transpose(A)。
- 当一个搜索模式
-
在RG_Matrix进行以下操作前,需要先获取锁mutex
- 对RG_Matrix进行resize操作
- 将delta_plus、delta_minus批处理更新matrix
4.2 GrB_Matrix in GraphBLAS
4.1节中提到,RG_Matrix使用了GrB_Matrix的两种存储格式:稀疏矩阵(GxB_SPARSE)和超稀疏矩阵(GxB_HYPERSPARSE)。
-
稀疏矩阵(GxB_SPARSE)
- 标准的CSR存储
- 这种格式要求矩阵元按行顺序存储,每一行中的元素可以乱序存储。
index pointrs存储每一行数据元素的起始位置indices这是存储每行中数据的列号,与data中的元素一一对应。- csr_matrix允许快速访问矩阵的行,但访问列的速度非常慢。
- 获取某一行非零元素的时间复杂度为O(1)
-
超稀疏矩阵(GxB_HYPERSPARSE)
- CSR矩阵的变体
- 当非零行非常少时,直接使用CSR矩阵会浪费存储。
- 增加一个数组:用于存储非零行的行号,且数组有序。
- 获取某一行非零元素的时间复杂度为O(logN),N为非零行的数量。
4.3 RG_Matrix for graph store
我们还是先从代码入手:
struct Graph {
RG_Matrix adjacency_matrix; // adjacency matrix, holds all graph connections
RG_Matrix *labels; // label matrices
RG_Matrix node_labels; // mapping of all node IDs to all labels possessed by each node
RG_Matrix *relations; // relation matrices
};
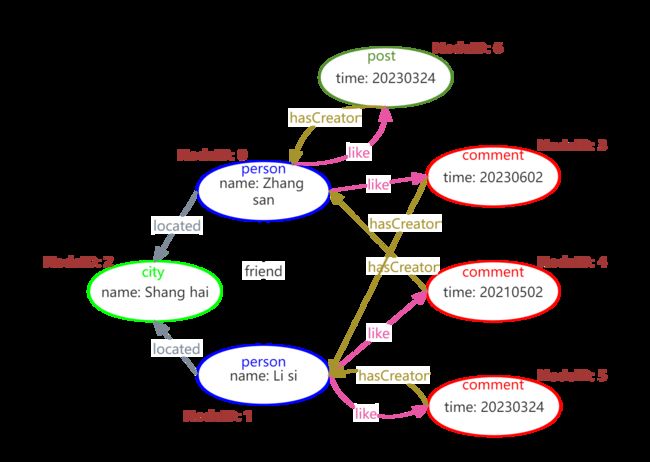
- 为了便于说明,我们以下图为例
-
Graph数据结构维护4种矩阵:矩阵均为NxN的方阵,N为顶点数。矩阵中的row、col对应上图中的NodeID
-
adjacency_matrix
-
邻接矩阵会标记图中的所有关系连接,关系类型不可知。
-
一张图仅对应一个adjacency_matrix
A d j = [ 0 1 1 1 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 ] Adj = \begin{bmatrix} 0 & 1 & 1 & 1 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} Adj= 0000101100101011000001000000010000001000001000000
-
-
labels
-
为了适应类型化节点,每个标签分配一个额外的矩阵,并且标签矩阵与沿主对角线的矩阵对称。
-
上图中存在4种类型的节点,也就存在4个label矩阵:city、person、post和comment。仅展示comment矩阵。
c o m m e n t = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ] comment = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} comment= 0000000000000000000000001000000010000000100000000 -
为什么要设置label矩阵?
当匹配
(person)-[like]->(comment)这个查询时,不仅仅会查询出person喜欢的comment,还会查询出post,这时候就需要comment矩阵过滤出最后的comment节点。
-
-
node_labels
-
在一些场景中,一个节点可能会对应多个label。每一个label也会有一个label_ID。
-
node_label矩阵是一个映射:将所有节点ID映射到每个节点拥有的所有label
-
一张图仅对应一个node_label矩阵
-
假设:city的label_ID为0,person的label_ID为1,comment的label_ID为2,post的label_ID为3,node_label矩阵如下:
c o m m e n t = [ 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 ] comment = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \end{bmatrix} comment= 0010000110000000011100000001000000000000000000000
-
-
relations
-
每个类型的关系都有自己的专用矩阵。
-
上图中存在4种类型的关系,也就存在4个relation矩阵:located、friend、hasCreator和like。仅展示like矩阵。
l i k e = [ 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] like = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} like= 0000000000000000000000100000010000001000001000000
-
-