漫步线性代数二——线性方程的几何形状

几何形状

理解这个主题的方法是举例说明。我们以两个极其简单的方程开始，可以说大家在没有学习线性代数课程的情况下都能解决。不过我希望可以给高斯一个机会：

2x−yx+y=1=5

我们可以按行或按列看待这个方程组。我希望大家两方面都能明白。

第一种方法主要看每个方程(行)。这是大家最熟悉的，对于两维的情况我们可以很快理解。方程 2x−y=1 表示 x−y 平面上的一条直线。该直线经过点 x=1,y=1 和 x=12,y=0 (也通过(2,3)和所有的中间点)。第二个方程 x+y=5 得到另一条线(图1a)。它的斜率是 dy/dx=−1 并且它与第一条线相交。

交点位于两条线上。它是这两个方程的唯一解。通过“消去法”可以快速的求出点 x=2,y=3 。

第二种方法是将线性系统看成列。两个独立方程实际是一个向量方程：

Column formx[21]+y[−11]=[15]

问题是找到组合左边列向量的组合，它产生了右边的向量。这些向量 (2,1),(−1,1) 由图1b中的粗线表示。未知量是与列向量相乘的 x,y 。整个想法可以从图中看出来，2倍的第一个列向量加上3倍的第二个列向量得到右边的结果。几何上这产生了著名的平行四边形。代数上这产生了方程右边正确的向量 (1,5) 。列图片证实了 x=2,y=3 。

对这个例子再花点时间，我会前进一步，令 n=3 。三个方程仍然是可控的并且他们有更多的变形：

Three planes2u4u−2u+−+v6v7v++w2w===5−29(1)

我们再次研究行或列，首先从行开始。每个方程描述了一个三维上的一个平面。第一个平面是 2u+v+w=5 ，如图2所示。它包含点 (52,0,0),(0,5,0),(0,0,5) 。它由任何三个点(只要他们不位于一条直线上)确定。

图1：行图像(两条线)和列图像(组合列)

将5变成10，平面 2u+v+w=10 将和一个平面平行。它包含点 (10,0,0),(0,10,0),(0,0,10) ，离原点 u=0,v=0,w=0 有两倍远。改变右边的数值将使平面产生移动，但依然与自己平行，平面 2u+v+w=0 通过原点。


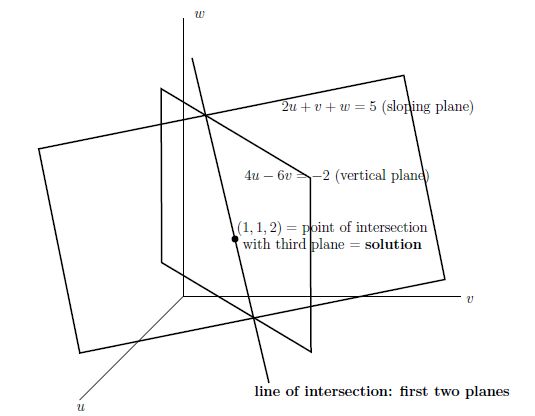
图2：行图像：三个线性方程表示的三个相交平面

第二个平面是 4u−6v=−2 。因为 w 可以取任意值，所以它是垂直的。w 的系数为零，但它仍然是3维空间中的一个平面。(方程 4u=3 或者更极端的 u=0 ，仍然描述的是一个平面。)图中展示了前两个平面相交。交于一条直线。在三维空间里，一条直线需要两个方程来确定；在 n 维空间里，它需要n−1 个方程。

最后，第三个平面与这条直线交于一点。第三个方程 −2u+7v+2w=9 表示一个平面(未绘制)，它通过点 u=1,v=1,w=2 。三个都相交的点 (1,1,2) 就是线性方程的解。

这个行图像如何扩展到 n 维呢？n个方程包含 n 个未知数。第一个方程仍然决定一个“平面”。不过它不再是三维空间里的二维平面；某种程度上来说，它是的维度是n−1。在 n 为空间里它必须是平的，并且非常薄。

如果时间是第四个维度，那么平面t=0削减了四维空间，产生了我们生活的三维宇宙(或相反，宇宙就是四维空间中 t=0 )。另一个平面是 z=0 ，这也是三维的；它就是普通的 x−y 平面，此时该平面覆盖了所有时间。这些三维平面也会相交！他们共享 t=0 处的 x−y 平面。我们现在降到两个维度，下一个平面留下了一条直线。最后，第四个平面留下了一个点。它是四维空间中四个平面的交点，它就是4个线性方程组的解。

如果这个来自相对论的例子在往前走一步，我就会陷入麻烦。针对这一点，线性代数可以解决任意数量的方程。第一个方程产生 n 为空间中n−1维的平面，第二个平面与它相交(我们希望如此)得到维数是 n−2 的更小集合。假如一切顺利，每个新平面(每个新方程)都减少一维度。到最后，当所有的 n 为平面都考虑进来后，交点的维数是零。它是一个点，位于所有平面上，并且其坐标满足所有的n个方程。它就是问题的解！

列向量与线性组合

我们转向列。这一次向量方程(与(1)的方程相等)是

Column formu⎡⎣⎢24−2⎤⎦⎥+v⎡⎣⎢1−67⎤⎦⎥+w⎡⎣⎢102⎤⎦⎥=⎡⎣⎢5−29⎤⎦⎥=b(2)

这些都是三维列向量。向量 b 由坐标是5,−2,9 的点确定。三维空间中的每个点都匹配一个向量，反之亦然。这是笛卡儿的思想，通过使用点的坐标它将几何变成代数。我们可以用列表示向量，或者我们可以列出它的成分如 b=(5,−2,9) ，或者我们可以用几何方式表示它，就是顶点在原点的箭头。你可以选择箭头，或点或三个数字。在六个维度，最简单的莫过于选择6个数。

当成分水平列出时，我们使用括号和逗号；当垂直书写时，用方括号(不带逗号)。真正重要的是向量加法和标量(一个数)乘法。在图2a中是向量加法，各部分分别相加：

Vector addition⎡⎣⎢500⎤⎦⎥+⎡⎣⎢0−20⎤⎦⎥+⎡⎣⎢009⎤⎦⎥=⎡⎣⎢5−29⎤⎦⎥

图像右边是乘以2(如果是-2，那么反转一下方向)：

Multiplication by scalars2⎡⎣⎢102⎤⎦⎥=⎡⎣⎢204⎤⎦⎥,−2⎡⎣⎢102⎤⎦⎥=⎡⎣⎢−20−4⎤⎦⎥

此外右侧的图是线性代数核心思想之一。它使用了两个基本操作；向量先是和数相乘，然后相加。这叫做线性组合，并且这种结合解决了我们的方程：

Linear combination1⎡⎣⎢24−2⎤⎦⎥+1⎡⎣⎢1−67⎤⎦⎥+2⎡⎣⎢102⎤⎦⎥=⎡⎣⎢5−29⎤⎦⎥

方程(2)要求乘数 u,v,w 产生右侧的 b 。这些数是u=1,v=1,w=2 。他们给出列的正确组合。在行图像(三个平面相交的)中也给出了点 (1,1,2)

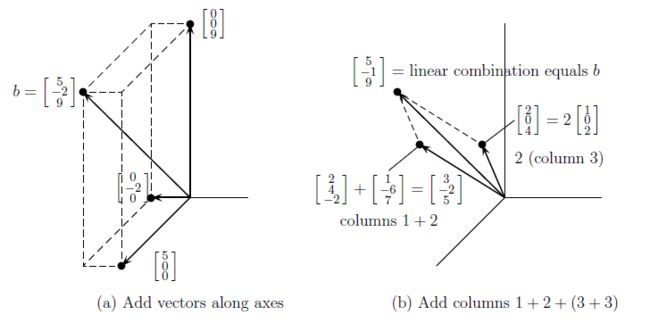
图3：列图像：列的线性组合等于 b

我们真正的目标是超越两个或三个维度，看到n维。对于 n 个未知量的n个方程，在行图像中有 n 个平面。在列图像中有n个向量，再加上右边的向量 b 。方程需要n列的线性组合等于 b 。当然对于某些方程可能不存在。比较矛盾的是，理解好案例的方式就是研究坏案例。因此当它不满足，也就是奇异的情形下，我们试着看看它的几何形状。

奇异情况

假设现在是三维空间，行图像中的三个平面不相交。那么将会有什么问题？一种可能是，两个平面平行。方程2u+v+w=5,4u+2v+2w=11不一致，平行的平面将无解(图4a所示)。在两维空间里，平行线是唯一的可能性。但在三维空间里，三个平面不想交的话会比较麻烦。

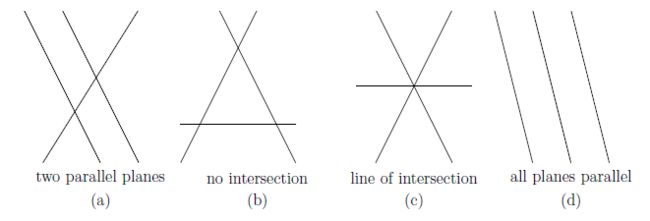
图4：奇异情况：(a)(b)(d)无解，(c)有无限个解

最常见的困难如图4b所示。平面构成了一个三角形。每一对平面都相交于一条直线，并且这些线都是平行的。第三个平面与其他平面不平行，但它与平行于他们的交线。这对应于一个奇异情况 b=(2,5,6) ：

No solution,as in Figure 4bu2u3u++vv+++w3w4w===256(3)

前两个方程左边相加得到第三个的左边，但右边 2+5≠6 。方程1加方程2减去方程3得到不可能命题 0=1 。因此方程组自相矛盾，高斯消元法将会系统地发现这个问题。

另一个与这个有关的奇异系统是有无限解。当最后那个方程的6换成7，三个方程结合起来得到 0=0 。现在第三个方程是前两个的和。这种情况下三个平面有一条共同直线(图4c)。改变右边的值将平行地移动图4b的平面，当 b=(2,5,7) 时，图像突然变得不同。最下面那条直线与另两条相交，这条线就是问题的解。图4c仍是奇异，但现在它是有太多的解，而不是太少。

极端的例子是三个平行平面。右边大部分情况下都没有解(图4d)。对于特殊的情况(像b=(0,0,0))整个平面都是解，因为三个平行平面移动成同一个平面。

当系统是奇异的时候，列图像会发生什么？方程左边仍有三列，并且我们试图组合他们得到 b 。

u⎡⎣⎢123⎤⎦⎥+v⎡⎣⎢101⎤⎦⎥+w⎡⎣⎢134⎤⎦⎥=b(4)

b=(2,5,7) 时，可能； b=(2,5,6) ，不可能。原因是这三列位于一个平面上。然后每个组合也都在这个平面上(过原点)。如果向量 b 不在平面上，那么没有解(图5)。这是迄今为止最有可能的情况；奇异系统一般都没有解。但是有一个机会，就是b 位于列组成的平面上。在这种情况下，有许多的解；三列可以有无限中组合得到 b 。图5b中的列图像对应于在图4c中的行图像。

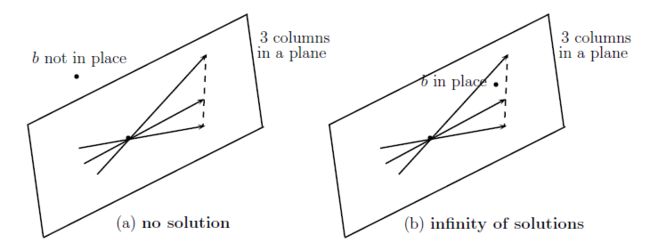
图5：奇异情况：b 位于三列确定的平面外或平面内

我们怎么知道三列位于同一平面内？答案之一是找出列的组合，使得他们相加等于零。经过一些计算，得到 u=3,v=1,w=−2 。三倍的第一列等于第二列加上两倍的第三列。第一列在第二列和第三列组成的平面内。只有两列是独立的。

向量 b=(2,5,7) 位于列1加列3构成的平面上，所以 (1,0,1) 是一种解。我们可以添加组合 (3,−1,−2) 给出了 b=0 。所以解是一整条直线，正如我们从行图像中看到的。

事实是，我们知道列组合得到零，因为行就是这样。这是一个数学事实，不是计算得到的，而且 n 维情况依然正确。如果n个平面没有交点，或有无限多个交点，那么$n$列位于同一个平面上。

如果行图像不成立，那么列图像同样如此。接下来几篇文章先讨论最重要问题-非奇异的情况，即有一个解。再然后研究一般情况，也许有很多解或根本没有。对于这两种情况，我们不需要矩阵符号和消除算法才能继续。