Python篇——数据结构与算法（第四部分：希尔排序及其讨论、计数排序、桶排序、基数排序）

1、希尔排序

• 希尔排序（shell sort）是一种分组插入排序算法
• 首先取一个整数d1=n/2，将元素分为d1个组，每组相邻两元素之间距离为d1，在各组内进行直接插入排序
• 取第二个整数d2=d1/2，重复上述分组排序过程，知道di=1，即所有元素在同一组内进行直接插入排序。
• 希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序

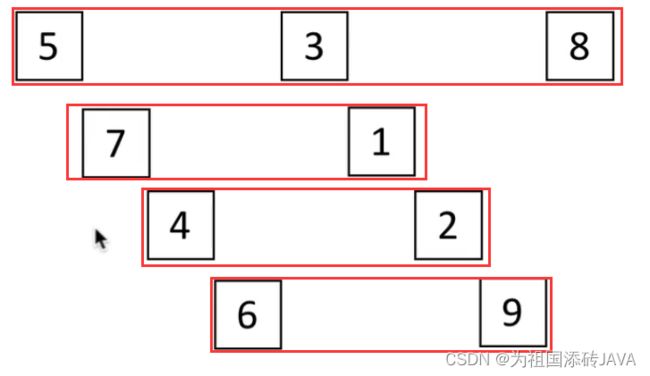
 例如：按照距离d1=n/2，将整个列表分为4组（例子中n=9）

（1） 分别为

• 第一组 5,3,8
• 第二组 7,1
• 第三组 4,2
• 第四组 6,9

（2）  然后在组内进行插入排序

 （3）然后在取整数d2=d1/2

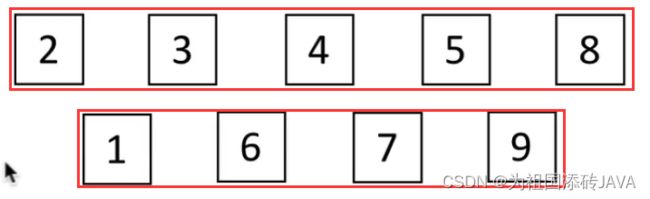
 （4）当d2的时候，将数组分为了两组，间隔为2的是一组，然后组内又进行插入排序

 （5）组内排序之后的结果图：

 （6）d3=d2/2，此时距离d3为1的为一组（当d3=1的时候相当于直接进行插入排序）

 （7）结果如图所示：

 （8）代码

def inseart_search_gap(list, gap):
    '''
    :param list: 列表
    :param gap: 分的组
    :return:
    '''
    for i in range(gap, len(list)):
        temp = list[i]
        j = i - gap
        while j >= 0 and list[j] > temp:
            list[j + gap] = list[j]
            j -= gap
        list[j + gap] = temp


def shell_sort(li):
    '''希尔排序'''
    d = len(li) // 2
    while d >= 1:
        inseart_search_gap(li, d)
        d //= 2

Note：

插入排序其实可以看成距离gap=1的情况

2、希尔排序的讨论

希尔排序的时间复杂度比较复杂，并且与选择的gap序列有关

 3、计数排序

• 对列表进行排序，已知列表中的数的取值范围都在0到100之间。设计时间复杂度为O（n）的算法

# 计数排序
import random


def count_sort(li, max_count=100):
    '''
    :param li:列表
    :param max_count:列表中最大取值
    '''
    count = [0 for _ in range(max_count + 1)]
    # 表示无论我遍历到第几次，不关心当前值是多少，而是一律输出0，因为取值范围是0-100，所以在生成列表的时候，我们要考虑到101
    for val in li:
        count[val] = count[val] + 1
    # 清空原列表，避免新建列表
    li.clear()
    for index, value in enumerate(count):
        for i in range(value):
            li.append(index)


li = [random.randint(0, 100) for _ in range(1000)]
print(li)
count_sort(li)
print(li)

Note：

• 缺陷如下：
  • 开辟列表空间浪费资源，比如取值范围是0-100就需要列表长度为100的列表
  • 需要知道给定数据的取值范围

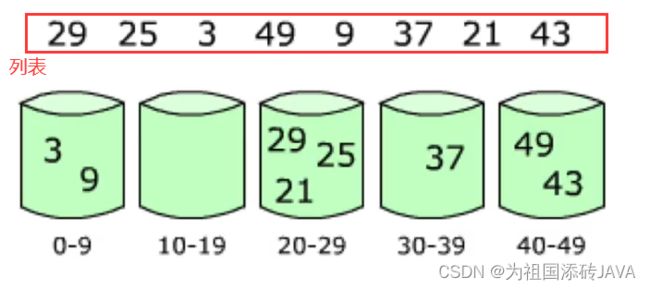
 4、桶排序

• 在计数排序中，如果元素的范围比较大（比如在1到1亿之间），如何改造算法
• 桶排序（Bucket Sort）：首先将元素分在不同的桶中，在对每个桶中的元素排序

# 桶排序
def bucket_sort(li, n=100, max_number=10000):
    '''
    :param li: 列表
    :param n: 分成多少桶
    :param max_number:最大取值范围
    '''
    buckets = [[] for _ in range(n)]  # 列表生成式(创建桶),例如：[[],[],[],...]
    for var in li:
        # 例如：每个桶放的范围是(max_number//n),假设var是86,那么它应该放在0号桶内，var整除(max_number//n)是0
        # 其中n-1表示最后一个桶,min()函数用于防止桶越界,即使数字为10000,也放入最后一个桶
        i = min(var // (max_number // n), n - 1)  # （表示var放到几号桶内）
        buckets[i].append(var)
        # for 循环结束元素都放入桶中
        for j in range(len(buckets[i]) - 1, 0, -1):  # 对第i号桶进行排序,j表示桶内最后一个元素开始,这里写0是因为前包后不包，范围到1号位置元素
            # [0,2,4,3] 假设放入的元素为3，需要j从最后遍历到2这个元素位置
            if buckets[i][j] < buckets[i][j - 1]:
                # 交换元素
                buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j]
            else:
                break
    sort_li = []  # 新建列表
    for buc in buckets:
        sort_li.extend(buc)  # 将一个列表加到另一个列表后面
    return sort_li

Note：

• 桶排序的表现取决于数据的分布。也就是要对不同数据排序时采用不同的分桶策略
• 平均情况时间复杂度：O（n+k）
• 最坏情况时间复杂度：O（n^2*k）
• 空间复杂度：O（nk）
• 数据排序部分可以根据实际需要进行优化

5、基数排序

 （1）多关键字排序

• 假如现在有一个员工表，要求按照薪资排序，年龄相同的员工按照年龄排序
  • 先按照年龄排序，再按照薪资进行稳定排序（稳定：相对位置不变）
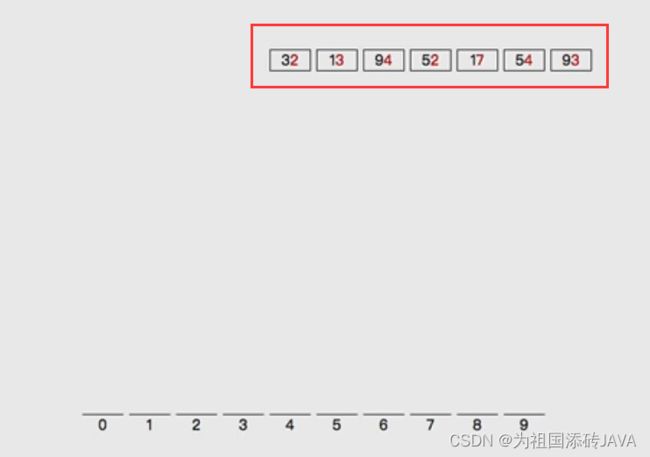
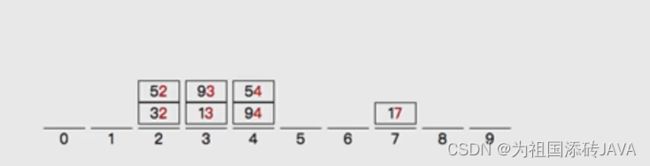
• 对32,13,94,52,17,54,93进行排序，是否可以看做多关键字排序

 Note：

• 先按照个位数分桶

 

• 然后依次输出

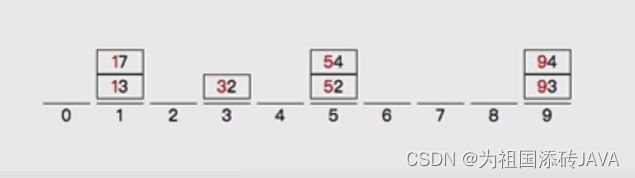
•  按照十位数分桶

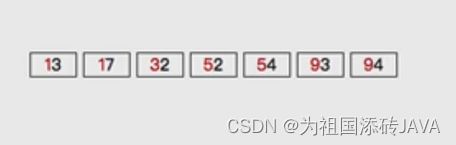
•  在依次输出

 （2）基数排序的实现

def radix_sort(li):
    max_num = max(li)  # max value 8->1 99->2 888->3 9999->4
    it = 0  # 迭代次数
    while 10 ** it <= max_num:
        buckets = [[] for _ in range(10)]
        for var in li:
            # 找某一位的数 987   it=1 取个位:987%10(取模)  it=2 取十位:987//10=98   98%10=8
            digit = (var // 10 ** it) % 10
            buckets[digit].append(var)
        # 分桶结束
        li.clear()
        for buc in buckets:
            li.extend(buc)
        # 重新写回li
        it += 1


import random

li = list(range(100))
random.shuffle(li)
radix_sort(li)
print(li)

Note：

• 时间复杂度：O（Kn）
• 空间复杂度：O（K+n）
• K表示数字位数