【算法题解】38. 括号的生成

这是一道 中等难度 的题
https://leetcode.cn/problems/generate-parentheses/

题目

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3 
输出：["((()))","(()())","(())()","()(())","()()()"] 

示例 2：

输入：n = 1 
输出：["()"] 

提示：

• $1<=n<=8$

---

递归解法一

分两步操作，先递归生成所有可能的组合，然后判断组合中的每个值是否合法有效。

生成所有的组合
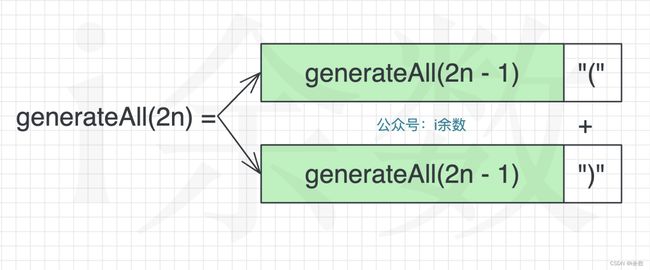
数字 n 代表生成括号的对数，那么最终生成的每一个结果中都会包含 2n 个括号。

从 1 到 2n 这些位置（或者说从 0 到 2n - 1 这些下标）上，每个位置的取值都是 “(” 或者 “)”。

那么 n 对括号的的所有组合 $generateAll(2n)$ 就应该是在 $generateAll(2n-1)$ 的基础上再加上最后一个位置的取值，即 $generateAll(2n-1)+“(”$ 和 $generateAll(2n-1)+“(”$ 的合集。

以此类推，直到遇到边界条件 n = 0 时，返回 $generateAll(0)$ = {“”}；

判断是否是有效的括号
判断括号是否有效可以使用栈的思路，遇到 “(” 则入栈，遇到 “)” 就将栈顶元素出栈并判断是否是“(”，如果不是那么肯定不合法直接返回 false。

最后如果栈中还有没出栈的元素，那么也不是合法的组合，因为没出栈的 “(” 没有与之相对应的 “)”。

相关题解有: 【算法题解】14. 有效的括号

Java 代码实现

class Solution {

    public List<String> generateParenthesis(int n) {
        if(n == 0){
            return Arrays.asList("");
        }
        
    	// 1. 生成所有可能的组合
    	// 2. 排除不合法的组合
        List<String> all = generateAll(2*n);
        
        return all.stream().filter(str -> isValid(str)).collect(Collectors.toList());
    }

    private List<String> generateAll(int size){
        if(size == 0){
            return Arrays.asList("");
        }

        List<String> all = new ArrayList();
        
        List<String> lastAll = generateAll(size - 1);
        for(String last : lastAll){
          
            all.add("(" + last);
            all.add(")" + last);
       
        }

        return all;
    }

    private boolean isValid(String str){
        Deque<Character> stack = new LinkedList<>();
        char[] ch = str.toCharArray();
       
        for(int i = 0; i < ch.length; i++){
            if(ch[i] == '('){
                stack.push(ch[i]);
            }else if(stack.isEmpty() || stack.pop() != '('){
                return false;
            }
        }

        return stack.isEmpty();

    }

   
}

Go 代码实现

func generateParenthesis(n int) []string {
    all := generateAll(2*n)
    ans := []string{}
    for _, str := range all {
        if isValid(st) {
            ans = append(ans, str)
        }
        
    }
    return ans
}

func generateAll(size int) []string {
    all := make([]string, 0)
    if size == 0 {
        all = append(all, "")
        return all
    }

    lastAll := generateAll(size - 1)
    for _, last := range lastAll {
        all = append(all, last + "(")
        all = append(all, last + ")")
    }
    return all
}

func isValid(s string) bool {
    n := len(s)
    stack := []byte{}
    for i := 0; i < n; i++ {
        if s[i] == ')' {
            if len(stack) == 0 || stack[len(stack)-1] != '(' {
                return false
            }
            stack = stack[:len(stack)-1]
        } else {
            stack = append(stack, s[i])
        }
    }
    return len(stack) == 0
}

复杂度分析

时间复杂度：$O(2^{2n}\ast n)$， 生成所有组合的时间复杂度为 $O(2^{2n})$ ，n 为生成括号的对数。判断是否合法的时间复杂度为 $O(n)$ ，总计$O(2^{2n}\ast n)$。

空间复杂度： $O(n)$，n 为递归调用栈的深度。

---

递归解法二：分治

所有的合法的组合，都应该是以左括号 “(” 开头的，且后面肯定会有一个右括号 “)” 与之匹配。即所有的组合都满足 (a)b 的格式，其中 a 和 b 可以为空或者其他任意有效的组合。

那么我们只要求的 a 和 b 的结果，然后拼成 (a)b 就得出最终的答案了，求 a 和 b 的结果同样是按照这个方式继续细分，还是递归的思路。

边界条件：n = 0 时，直接返回空，也可以把 n = 1 加上去，直接返回“()”。

Java 代码实现

class Solution {
    private Map<Integer, List<String>> cache = new HashMap<>();

    public List<String> generateParenthesis(int n) {
        List<String> ans;
        if(cache.containsKey(n)){
            return cache.get(n);
        }
        if(n == 0){
            ans = Arrays.asList("");
        }else if(n == 1){
            ans = Arrays.asList("()");
        }else{
            ans = new ArrayList<>();
            // a + b = n - 1
            for(int a = 0; a < n; a ++){
                int b = n - 1 - a;
                List<String> aList = generateParenthesis(a);
                List<String> bList = generateParenthesis(b);
                for(String aTemp : aList){
                    for(String bTemp : bList){
                        ans.add("(" + aTemp +")" + bTemp);
                    }
                }
            }

        }

        cache.put(n, ans);
        return ans;
    }
   
}

Go 代码实现

func generateParenthesis(n int) []string {
    ans := []string{}
    if n == 0 {
        ans = append(ans, "")
        return ans;
    }
    if n == 1 {
        ans = append(ans, "()")
        return ans;
    }

    for a := 0; a < n; a++ {
        b := n - 1 - a

        aList := generateParenthesis(a)
        bList := generateParenthesis(b)

        for _, aTemp := range aList {
            for _, bTemp := range bList {
                ans = append(ans, "(" + aTemp + ")" + bTemp)
            }
        }
    }

    return ans
}

---

深度优先搜索

同解法一的思路一样，先生成所有可能的组合，然后再判断是否合法。不一样的是生成时使用 深度优先搜索 的思路。

递归函数：每一个位置都有 “(” 或者 “)”两个选项。

边界条件：当走到最后一个位置的时候返回。

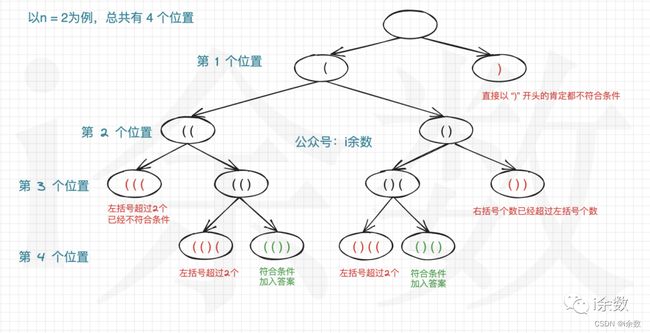
关于优化剪枝：

1. 直接以右括号 “)” 开头的肯定都不合法，直接排除。
2. 当生成的组合中，无论是 "(" 还是 ")" 的个数已将超过一半（n个），那么肯定是不合法的了，可以提前排除掉。
3. 当遇到 ")" 的个数 大于 "(" 的个数时，那么多出来的那个右括号已经无法匹配了，可以提前排除掉。

关于判断合法性：
只要能走到最后，且左右括号的个数都是 n，那么肯定就是合法的，无需再判断合法性。

因为不合法的几种情况都通过剪枝剪掉了：

1. 左右括号的个数不对，已经通过 剪枝条件2 剪掉。
2. 左右括号个数相等的情况下，只要是不合法的，其前面的某一个时刻，必然是多出来一个右括号“)”是匹配不上的，已经通过 剪枝条件3 剪掉了。如某一时刻为 "a)" ，其中 a 是合法的组合，那么 “a)” 就已经不合法了。

Java 代码实现

class Solution {
 
    private List<String> ans = new ArrayList<>();
    private int size;

    public List<String> generateParenthesis(int n) {
        this.size = n;
        char[] ch = new char[2 * n];
        ch[0] = '(';
        int left = 1, right = 0;
        // 第一个位置肯定是 ‘(’
        dfs(ch, 1, 1, 0);
        return ans;
    }

    private void dfs(char[] ch, int index, int left, int right){
        if(left > size){
            return;
        }
        if(right > size){
            return;
        }

        if(right > left){
            return;
        }
        // 边界条件
        if(index == 2 * size){
            ans.add(new String(ch));
            return;
        }

        // 每个位置都有 2 种可能
        ch[index] = '(';
        dfs(ch, index + 1, left + 1, right);


        ch[index] = ')';
        dfs(ch, index + 1, left, right + 1);

        return;
    }   
}

Go 代码实现

var (
    ans []string
    size int
    )
func generateParenthesis(n int) []string {
    ans = []string{}
    size = n
    // 以左括号开始
    path := "("

    dfs(path, 1, 1, 0)

    return ans
}

func dfs(path string, index int, left int, right int){
    if left > size {
        return
    }
    if right > size {
        return
    }
    if(right > left){
        return
    }

    if index == (2 * size) {
        ans = append(ans, path)
    }

  
    dfs(path + "(", index + 1, left + 1, right)
    
    dfs(path + ")", index + 1, left, right + 1)

}

剪枝后优化效果非常明显。

复杂度分析

时间复杂度： $O(2^{2n})$。总的节点个数为 $2^{2n+1}-1$ 个，除掉右半边，可以按照 $2^{2n}$个计算。

空间复杂度： $O(n)$，ch 数组长度为 2n，递归深度也是 2n。