2023/05/08~14 刷题记录
A - Plus and Multiply
题解:
题目说可以将集合里面的数字 *a 或者 +b 操作,并将新的值放进集合中,首先想到 dfs 暴力求解,但是太暴力了,直接 时间超限 。通过观察我们可以知道,要求 n 是否在集合中,如果在 一定会存在 一个 x1、x2 使得 a(乘x1次) + b(加x2次) == n。为什么不会出现先加上 b 再乘上 a 的情况呢?因为如果你先加上了一个 b,那么后面乘上 a 相当于是 加了 a 个 b。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- != 0) {
long n = sc.nextInt();
long a = sc.nextInt();
long b = sc.nextInt();
boolean k = false;
if (a == 1) {
if (n % b == 1 || b == 1) System.out.println("Yes");
else System.out.println("No");
continue;
}
for (int i = 1; i <= n; i *= a) {
if ((n - i) % b == 0)
k = true;
if (k)
break;
}
if (k)
System.out.println("Yes");
else
System.out.println("No");
}
}
}
B - Air Conditioner
题解:
那么我们可以按顾客到达的顺序来处理。 维护温度可能的区间[L,R]。从顾客i-1到i时,过去的时间d = t - t(i-1),温度可能的区间[L, R]=[L - d,R+d]。
又因为要满足第i个顾客的需求,所以我们将这个区间与[l,r;]取交集即可。取交集:[L,R] ∩ [l, ri]=[max(L, li), min(R, ri)]
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- != 0) {
int n = sc.nextInt();
int m = sc.nextInt();
ArrayList<Guest> guests = new ArrayList<>(n);
for (int i = 0; i < n; i++)
guests.add(new Guest(sc.nextInt(), sc.nextInt(), sc.nextInt()));
// 根据时间排序
guests.sort((o1, o2) -> o1.getT() - o2.getT());
int l = m, r = m, now = 0;
boolean k = false;
for (Guest guest : guests) {
int hh = guest.getH();
int ll = guest.getL();
int time = guest.getT();
int x = time - now;
now = time;
l -= x;
r += x;
k = true;
// 取区间最小值。
// 一个是可以到达的最低和最高温度,一个是为满足客户可以到达的最低最高温度
l = Math.max(l, ll);
r = Math.min(r, hh);
if (l > r) {
k = false;
break;
}
}
if (k)
System.out.println("YES");
else
System.out.println("NO");
}
}
}
class Guest {
int t, l, h;
public int getT() {
return t;
}
public void setT(int t) {
this.t = t;
}
public int getL() {
return l;
}
public void setL(int l) {
this.l = l;
}
public int getH() {
return h;
}
public void setH(int h) {
this.h = h;
}
public Guest(int t, int l, int h) {
this.t = t;
this.l = l;
this.h = h;
}
}
C - Theatre Square
题解:
分别求出该广场的长和宽分别需要多长的石板,然后将 长和宽 相乘即可。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int a = sc.nextInt();
// 求解长和宽,并相乘输出
System.out.println((long) Math.ceil((double) m / a) * (long) Math.ceil(n / (double) a));
}
}
D - Bargaining Table
题解:
使用 二维前缀和 取计算矩阵周长是否全是 ‘0‘,也就是是否存在 ‘1’。如果不存在 ‘1’,则尝试作为答案,判断大小。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
sc.nextLine();
// 输入地图,并计算 二维前缀和
int[][] map = new int[n + 1][m + 1];
sum = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
String s = sc.nextLine();
// 计算 二维前缀和
int temp = 0;
for (int j = 1; j <= m; j++) {
map[i][j] = Integer.parseInt(String.valueOf(s.charAt(j - 1)));
temp += map[i][j];
sum[i][j] = sum[i - 1][j] + temp;
}
}
// 全遍历 并剪枝
int ans = 0;
for (int x1 = 1; x1 <= n; x1++)
for (int y1 = 1; y1 <= m; y1++)
if (map[x1][y1] == 0)
for (int x2 = x1; x2 <= n; x2++)
for (int y2 = y1; y2 <= m; y2++)
if (fun(x1, y1, x2, y2) == 0)
ans = Math.max(ans, ((x2 - x1 + 1) + (y2 - y1 + 1)) * 2);
System.out.println(ans);
}
static int n, m;
//存储 二维前缀和
static int[][] sum;
// 求 (x1, y1) 到 (x2, y2) 之间的二维前缀和
static int fun(int x1, int y1, int x2, int y2) {
return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}
}
E - Coins
题解:
求解出素数,因为一个合数就是由很多素数组成,从小到大 一个一个 除尽 依次输出即可。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.print(n + " ");
ArrayList<Integer> primeNumbers = getPrimeNumbers(n);
// 遍历每一个素数, 因为合数就是由若干个素数组成,让这个数除每个素数
for (Integer primeNumber : primeNumbers) {
while (n % primeNumber == 0) {
n /= primeNumber;
System.out.print(n + " ");
if (n == 1)
break;
}
}
}
// 求素数,埃筛
private static ArrayList<Integer> getPrimeNumbers(int n) {
ArrayList<Integer> primeNumbers = new ArrayList<>();
int len = n + 1;
// 初始化素数
int[] temp = new int[len];
temp[0] = 1;
temp[1] = 1;
for (int i = 2; i < len; i++) {
if (temp[i] == 0) {
for (int j = i * 2; j < len; j += i)
temp[j] = 1;
primeNumbers.add(i);
}
}
return primeNumbers;
}
}
F - Alice, Bob and Chocolate
题解:
使用 双指针 循环遍历,L 代表 左指针 指向左下标,R 代表 右指针 指向右下标
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++)
a[i] = sc.nextInt();
// 使用 双指针 指向数组,依次遍历
int l = 0, r = n - 1;
while (l + 1 < r) {
if (a[l] < a[r]) {
a[r] -= a[l];
l++;
} else if (a[l] > a[r]) {
a[l] -= a[r];
r--;
} else {
l++;
r--;
}
}
// 因为 下标 比 序号 小 1,所以下标需要加一 变成个数
l++;
// 同时,因为他们可能同时到达同一个 “巧克力棒”,而女士优先
// 故取 l 作为 Alice 答案,n-l 作为 Bob 答案
System.out.println(l + " " + (n - l));
}
}
H - Sale
题解:
题目就是要求我们求出 在 m 个电器的范围内,最大可以 “赚” 多少钱,也就是看 电视机 的负数价格有多少。
很显然,快排,然后遍历。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
ArrayList<Integer> a = new ArrayList<>();
for (int i = 0; i < n; i++)
a.add(sc.nextInt());
// 快排
Collections.sort(a);
// 遍历 至多 m 个,求负数之和为多少
int ans = 0;
for (int i = 0; i < m; i++)
if (a.get(i) < 0)
ans -= a.get(i);
else
break;
System.out.println(ans);
}
}
I - Laptops
题解:
使用快排对 笔记本的价格 进行排序,然后再依次遍历,判断 每一台计算机 是否 比前一台计算机质量高。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
ArrayList<Goods> goods = new ArrayList<Goods>();
for (int i = 0; i < n; i++)
goods.add(new Goods(sc.nextInt(), sc.nextInt()));
// 根据 笔记本 的价格 快速排序
goods.sort((o1, o2) -> o1.a - o2.a);
boolean k = false;
// 如果有一台 笔记本 在价值低的情况下,反而质量更好 就标记
// ps:在这里为什么不要 把每台计算机前面的所有计算机都比较一下质量呢?
// 因为 这个质量一定是呈现递增的趋势,不然 循环已经终止了(也就是说,前一台计算机一定是 前面所有计算机中 质量最好的)
for (int i = 1; i < goods.size(); i++) {
if (goods.get(i - 1).b > goods.get(i).b) {
k = true;
break;
}
}
if (k)
System.out.println("Happy Alex");
else
System.out.println("Poor Alex");
}
}
class Goods {
int a, b;
Goods(int a, int b) {
this.a = a;
this.b = b;
}
}
J - Trust Nobody
题解:
注意题目中所说的 “至少”。
通过分析题目,我们了解到了,假设一组数据中答案是 5,则 说大于 5 的人则在说假话。
因此,我们使用桶排 统计所有人说的 x 的次数,使用 a[x] 表示。
再遍历的过程中 使用前缀和优化循环次数。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- != 0) {
int n = sc.nextInt(), x;
// 桶排 统计所有人说的 x 的次数,使用 a[x] 表示。
int[] a = new int[n];
for (int i = 0; i < n; i++) {
x = sc.nextInt();
// 如果 大于等于 n,则肯定在说谎,不必统计
if (x < n)
a[x]++;
}
// 前缀和 统计结果,如果没有答案输出 -1
int ans = -1, sum = 0;
for (int i = 0; i < n; i++) {
sum += a[i];
if (i == n - sum) {
ans = i;
break;
}
}
System.out.println(ans);
}
}
}
K - Dreaming of Freedom
题目大意:
题解:
模拟题。
注意剪枝,时间复杂度。
如果 “程序员” 的个数 n 是一个合数,也就是可以被素数整除的话(同时这个素数得 小于 题目的个数 m)则可以一直选下去,没有尽头。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt(), n, m;
boolean k;
while (t-- != 0) {
n = sc.nextInt();
m = sc.nextInt();
if (n == 1 || m == 1) {
System.out.println("YES");
continue;
} else if (m >= n) {
System.out.println("NO");
continue;
}
// 注意剪枝 i <= n / i
k = false;
for (int i = 2; i <= m && i <= n / i; i++) {
if (n % i == 0) {
k = true;
break;
}
}
if (!k)
System.out.println("YES");
else
System.out.println("NO");
}
}
}
L - Lunatic Never Content
题解:
这道题不难,但解决前需要知道几个知识点:
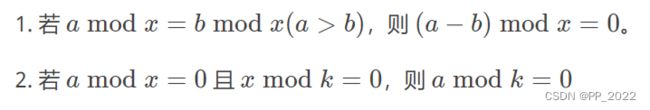
因此,这道题变成了找所有对数差的最大公因数。
除此之外,x 可以为无限大的情况就是数组 a 本身是回文的情况,需要特判输出 0。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- != 0) {
int n = sc.nextInt();
ArrayList<Integer> a = new ArrayList<>(n);
for (int i = 0; i < n; i++)
a.add(sc.nextInt());
Set<Integer> ans = new HashSet<>(n);
for (int i = 0; i < n / 2; i++)
ans.add(Math.abs(a.get(i) - a.get(n - i - 1)));
// 如果 都是 0 说明 这个本身就是一个回文数,可以被无限大除 输出 0
ans.remove(0);
if (ans.size() > 0)
System.out.println(fun(ans));
else
System.out.println(0);
}
}
// 求解一个集合中所有数的 最小公约数
static int fun(Set<Integer> ans) {
int result = ans.iterator().next();
for (Integer an : ans) {
int min = Math.min(result, an);
while (result % min != 0 || an % min != 0)
min--;
result = min;
}
return result;
}
}
M - Running Miles
题解:
两个指针指向 左右最合适的边界点。
遍历每个点寻找答案,把每个点(去首尾)当作为中间点,加上 左右边界 最合适的点 求解答案
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- != 0) {
int n = sc.nextInt();
ArrayList<Integer> a = new ArrayList<>(n);
for (int i = 0; i < n; i++)
a.add(sc.nextInt());
// 求解 只考虑 后面 i 个元素时,r 取哪个值最合适,存储哪个值的下标
int[] last = new int[n];
last[n - 1] = n - 1;
for (int i = 1; i < n; i++)
last[n - 1 - i] = a.get(last[n - i]) - last[n - i] > a.get(n - i) - (n - i) ? last[n - i] : n - i;
// 两个指针指向 左右最合适的边界点。
int l = 0, r, ans = 0;
// 遍历每个点寻找答案,把每个点(去首尾)作为中间点,加上 左右边界 最合适的点 求解答案
for (int i = 1; i < a.size() - 1; i++) {
r = last[i];
ans = Math.max(ans, a.get(l) + a.get(i) + a.get(r) + l - r);
if (a.get(l) + l - i <= a.get(i))
l = i;
}
System.out.println(ans);
}
}
}











