AtCoder Beginner Contest 300——A-G题讲解

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻讲解一下AtCoder Beginner Contest 300这场比赛的A-G题！

===========================================================================================

A - N-choice question

原题

Problem Statement

Given integers $A$ and $B$, find $A+B$.

This is a $N$-choice problem; the $i$-th choice is $C_i$.

Print the index of the correct choice.

Constraints

All values in the input are integers.
$1\le N\le 300$
$1\le A,B\le 1000$
$1\le C_i\le 2000$
$C_i$ are pairwise distinct. In other words, no two choices have the same value.
There is exactly one $i$ such that $A+B=C_i$. In other words, there is always a unique correct choice.

Input

The input is given from Standard Input in the following format:

$N$ $A$ $B$
$C_1$ $C_2$ $\dots$ $C_N$

Output

Print the answer as an integer.

Sample Input 1

3 125 175
200 300 400

Sample Output 1

2

We have $125+175=300$.

The first, second, and third choices are $200$, $300$, and $400$, respectively.

Thus, the $2$-nd choice is correct, so $2$ should be printed.

Sample Input 2

1 1 1
2

Sample Output 2

1

The problem may be a one-choice problem.

Sample Input 3

5 123 456
135 246 357 468 579

Sample Output 3

5

题目大意

就是找出C序列中第几个数是A+B的和。

---

思路

太简单，不写了，直接见代码

代码

#include 

using namespace std;

int main()
{
	int n, a, b;
	
	cin >> n >> a >> b;
	
	int c = a + b, t;
	for (int i = 1; i<= n; i ++)
	{
		cin >> t;
		if (t == c)
		{
			cout << i << endl;
			return 0;
		}
	}
}

B - Same Map in the RPG World

原题

Problem Statement

Takahashi is developing an RPG. He has decided to write a code that checks whether two maps are equal.

We have grids $A$ and $B$ with $H$ horizontal rows and $W$ vertical columns. Each cell in the grid has a symbol # or . written on it.

The symbols written on the cell at the $i$-th row from the top and $j$-th column from the left in $A$ and $B$ are denoted by $A_{i,j}$ and $B_{i,j}$, respectively.
The following two operations are called a vertical shift and horizontal shift.
For each $j=1,2,\dots ,W$, simultaneously do the following:
simultaneously replace $A_{1,j},A_{2,j},\dots ,A_{H-1,j},A_{H,j}$ with $A_{2,j},A_{3,j},\dots ,A_{H,j},A_{1,j}$.
For each $i=1,2,\dots ,H$, simultaneously do the following:
simultaneously replace $A_{i,1},A_{i,2},\dots ,A_{i,W-1},A_{i,W}$ with $A_{i,2},A_{i,3},\dots ,A_{i,W},A_{i,1}$.
Is there a pair of non-negative integers $(s,t)$ that satisfies the following condition? Print Yes if there is, and No otherwise.
After applying a vertical shift $s$ times and a horizontal shift $t$ times, $A$ is equal to $B$.
Here, $A$ is said to be equal to $B$ if and only if $A_{i,j}=B_{i,j}$ for all integer pairs $(i,j)$ such that $1\le i\le H$ and $1\le j\le W$.

Constraints

$2\le H,W\le 30$
$A_{i,j}$ is # or ., and so is $B_{i,j}$.
$H$ and $W$ are integers.

Input

The input is given from Standard Input in the following format:

$H$ $W$
$A_{1,1}{A}_{1,2}\dots A_{1,W}$
$A_{2,1}{A}_{2,2}\dots A_{2,W}$
$⋮$
$A_{H,1}{A}_{H,2}\dots A_{H,W}$
$B_{1,1}{B}_{1,2}\dots B_{1,W}$
$B_{2,1}{B}_{2,2}\dots B_{2,W}$
$⋮$
$B_{H,1}{B}_{H,2}\dots B_{H,W}$

Output

Print Yes if there is a conforming integer pair $(s,t)$; print No otherwise.

Sample Input 1

4 3
..#
...
.#.
...
#..
...
.#.
...

Sample Output 1

Yes

By choosing $(s,t)=(2,1)$, the resulting $A$ is equal to $B$.

We describe the procedure when $(s,t)=(2,1)$ is chosen. Initially, $A$ is as follows.

..#
...
.#.
...

We first apply a vertical shift to make $A$ as follows.

...
.#.
...
..#

Then we apply another vertical shift to make $A$ as follows.

.#.
...
..#
...

Finally, we apply a horizontal shift to make $A$ as follows, which equals $B$.

#..
...
.#.
...

Sample Input 2

3 2
##
##
#.
..
#.
#.

Sample Output 2

No

No choice of $(s,t)$ makes $A$ equal $B$.

Sample Input 3

4 5
#####
.#...
.##..
..##.
...##
#...#
#####
...#.

Sample Output 3

Yes

Sample Input 4

10 30
..........##########..........
..........####....###.....##..
.....##....##......##...#####.
....####...##..#####...##...##
...##..##..##......##..##....#
#.##....##....##...##..##.....
..##....##.##..#####...##...##
..###..###..............##.##.
.#..####..#..............###..
#..........##.................
................#..........##.
######....................####
....###.....##............####
.....##...#####......##....##.
.#####...##...##....####...##.
.....##..##....#...##..##..##.
##...##..##.....#.##....##....
.#####...##...##..##....##.##.
..........##.##...###..###....
...........###...#..####..#...

Sample Output 4

Yes

题目大意

两个仅由# 和 . 组成的矩阵A和B，A的各行可以同时向右转动，最后边的列到最左边，各列可以同时向上转动，最上面的到最下面，问这种变动能否使得A和B相等。

---

思路

通过遍历和模拟就可以完成，比较简单，直接见代码。

---

代码

#include
using namespace std;
const int N = 35;

string a[N], b[N], mycp[N], mydp[N];
bool flag;
int nop;

int main(){
    int h,w;
    cin >> h >> w;
    for(int i =1 ;i <= h; i ++) cin >> a[i];
    
    for(int i =1 ;i <= h; i ++) cin >> b[i];
    
    for(int i =1 ;i <= h; i ++) mycp[i] = a[i] + a[i];
   
    
    for(int i = 1; i <= h ;i ++){
     
        for(int j = 0; j <= w*2 -1 ;j ++){
            
            for(int x = 1; x <= h; x++){
        
                if(mycp[i].substr(j,w) ==  b[x]){
                    nop = 1;
                    for(int t = i; t <= h; t++) mydp[nop ++] = mycp[t].substr(j,w);
                        
                    for(int t = 1 ; t < i ; t++) mydp[nop ++] = mycp[t].substr(j,w);
                    
                    flag = 0;
                    for(int t = 1; t <= nop ; t ++) if(mydp[t] != b[t]) flag = 1;
                    
                    if(flag == 0){
                        cout <<"Yes"<<endl;
                        return 0;
                    } 
                }
            }
        }
    }
    cout << "No" <<endl;
    return 0;
}

C - Cross

原题

Problem Statement

We have a grid with $H$ horizontal rows and $W$ vertical columns. We denote by $(i,j)$ the cell at the $i$-th row from the top and $j$-th column from the left of the grid.

Each cell in the grid has a symbol # or . written on it. Let $C[i][j]$ be the character written on $(i,j)$. For integers $i$ and $j$ such that at least one of $1\le i\le H$ and $1\le j\le W$ is violated, we define $C[i][j]$ to be ..
$(4n+1)$ squares, consisting of $(a,b)$ and $(a+d,b+d),(a+d,b-d),(a-d,b+d),(a-d,b-d)$ $(1\le d\le n,1\le n)$, are said to be a cross of size $n$ centered at $(a,b)$ if and only if all of the following conditions are satisfied:
$C[a][b]$ is #.
$C[a+d][b+d],C[a+d][b-d],C[a-d][b+d]$, and $C[a-d][b-d]$ are all #, for all integers $d$ such that $1\le d\le n$,
At least one of $C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1]$, and $C[a-n-1][b-n-1]$ is ..
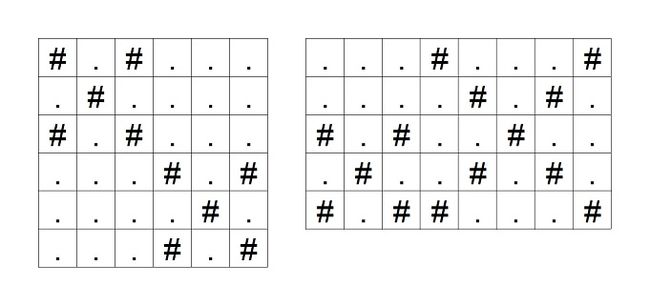
For example, the grid in the following figure has a cross of size $1$ centered at $(2,2)$ and another of size $2$ centered at $(3,7)$.

The grid has some crosses. No # is written on the cells except for those comprising a cross.

Additionally, no two squares that comprise two different crosses share a corner. The two grids in the following figure are the examples of grids where two squares that comprise different crosses share a corner; such grids are not given as an input. For example, the left grid is invalid because $(3,3)$ and $(4,4)$ share a corner.

Let $N=\min (H,W)$, and $S_n$ be the number of crosses of size $n$. Find $S_1,S_2,\dots ,S_N$.

Constraints

$3\le H,W\le 100$
$C[i][j]$ is # or ..
No two different squares that comprise two different crosses share a corner.
$H$ and $W$ are integers.

Input

The input is given from Standard Input in the following format:

$H$ $W$
$C[1][1]C[1][2]\dots C[1][W]$
$C[2][1]C[2][2]\dots C[2][W]$
$\vdots$
$C[H][1]C[H][2]\dots C[H][W]$

Output

Print $S_1,S_2,\dots$, and $S_N$, separated by spaces.

Sample Input 1

5 9
#.#.#...#
.#...#.#.
#.#...#..
.....#.#.
....#...#

Sample Output 1

1 1 0 0 0

As described in the Problem Statement, there are a cross of size $1$ centered at $(2,2)$ and another of size $2$ centered at $(3,7)$.

Sample Input 2

3 3
...
...
...

Sample Output 2

0 0 0

There may be no cross.

Sample Input 3

3 16
#.#.....#.#..#.#
.#.......#....#.
#.#.....#.#..#.#

Sample Output 3

3 0 0

Sample Input 4

15 20
#.#..#.............#
.#....#....#.#....#.
#.#....#....#....#..
........#..#.#..#...
#.....#..#.....#....
.#...#....#...#..#.#
..#.#......#.#....#.
...#........#....#.#
..#.#......#.#......
.#...#....#...#.....
#.....#..#.....#....
........#.......#...
#.#....#....#.#..#..
.#....#......#....#.
#.#..#......#.#....#

Sample Output 4

5 0 1 0 0 0 1 0 0 0 0 0 0 0 0

题目大意

从给点的矩阵中找由 #组成的图形，其中从中心 #往外一共有几层，按层数进行统计，分别输出1层、2层、3层……n层的个数。

---

思路

这道题我们可以枚举每一个#，对于每一个#，可以进行X型扩展，扩展的时候注意处理边界！（详情见代码吧！）

---

代码

#include 

using namespace std;

const int N = 1e2 + 10;

int h, w;
char c[N][N];
int s[N];

int main()
{
	cin >> h >> w;
	
	for (int i = 1; i <= h; i ++)
		for (int j = 1; j <= w; j ++)
			cin >> c[i][j];
			
	for (int i = 2; i < h; i ++)
		for (int j = 2; j < w; j ++)
			if (c[i][j] == '#')
			{
				int deep = 0;
				while (i + deep + 1 <= h && i - deep + 1 >= 1 && j - deep + 1 >= 1 && j + deep + 1 <= w && c[i + deep + 1][j - deep - 1] == '#' && c[i + deep + 1][j + deep + 1] == '#' && c[i - deep - 1][j - deep - 1] == '#' && c[i - deep - 1][j + deep + 1] == '#')
					deep ++;
				s[deep] ++;
			}
	
	for (int i = 1; i <= min(h, w); i ++)
		cout << s[i] << " ";
		
	return 0;
}

D - AABCC

原题

Problem Statement

How many positive integers no greater than $N$ can be represented as $a^2\times b\times c^2$ with three primes $a,b$, and $c$ such that a < b < c ?

Constraints

$N$ is an integer satisfying $300\le N\le 10^{12}$.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print the answer as an integer.

Sample Input 1

1000

Sample Output 1

3

The conforming integers no greater than $1000$ are the following three.
$300=2^2\times 3\times 5^2$
$588=2^2\times 3\times 7^2$
$980=2^2\times 5\times 7^2$

Sample Input 2

1000000000000

Sample Output 2

2817785

题目大意

对于质数$a,b$, and $c$， a < b < c，问$a^2\times b\times c^2$组成的小于N的数的个数。

---

思路

方法一：
由于$a^2\times b\times c^2\le N$，且a < b < c，
所以$a^5\le N$，$a\le 400$
对于b和c只需要遍历到$10^6$就足够了。
所以先把$10^6$的所有质数求出来，a只取前78个，其它的直接遍历计算就可以了。
方法二：
基本于方法一的思路 一样，只是对于C可以采用二分进行快速计算。

代码

方法一：

#include 
#include 
#include 
#define int long long 

using namespace std;

const int  N = 1e6 + 10;

int n;
vector<int> prime;
bool st[N];

void div(int x)
{
    for (int i = 2; i <= x; i ++)
    {
        if (!st[i]) prime.push_back(i);
        for (int j = 0; prime[j] <= x / i; j ++)
        {
            st[i * prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
}

signed main()
{
	cin >> n;
	
	div(1000000);
	
	int res = 0;
	for (int i = 0; i < 78; i ++)
		for (int j = i + 1; prime[i] * prime[j] * prime[j] * prime[i] * prime[j] <= n; j ++)
			for (int k = j + 1; prime[i] * prime[j] * prime[k] * prime[i] * prime[k] <= n; k ++)
				res ++;
					
	cout << res << endl;
	return 0;
}

方法二：

#include 
#include 
#include 
#define int long long 

using namespace std;

const int  N = 1e6 + 10;

int n;
vector<int> prime;
bool st[N];

void div(int x)
{
    for (int i = 2; i <= x; i ++)
    {
        if (!st[i]) prime.push_back(i);
        for (int j = 0; prime[j] <= x / i; j ++)
        {
            st[i * prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
}

signed main()
{
	cin >> n;
	
	div(290000);
	
	int res = 0;
	for (int i = 0; i < prime.size(); i ++)
		for (int j = i + 1; j < prime.size() && prime[j] * prime[i] <= 1e6; j ++)
		{
			int l = j + 1, r = prime.size() - 1, t = 0;
			while (l <= r)
			{
				int mid = l + r + 1 >> 1;
				if (prime[mid] * prime[i] <= 1e6 && (int)1ll * prime[i] * prime[j] * prime[mid] * prime[i] * prime[mid] <= n) l = mid + 1;
				else r = mid - 1;
			}
			
			res += l - j - 1;
		}
		
	cout << res << endl;
	return 0;
}

E - Dice Product 3

原题

Problem Statement

You have an integer $1$ and a die that shows integers between $1$ and $6$ (inclusive) with equal probability.

You repeat the following operation while your integer is strictly less than $N$:

• Cast a die. If it shows $x$, multiply your integer by $x$.

Find the probability, modulo $998244353$, that your integer ends up being $N$.

How to find a probability modulo $998244353$?
We can prove that the sought probability is always rational.
Additionally, under the constraints of this problem, when that value is represented as $\frac{P}{Q}$ with two coprime integers $P$ and $Q$, we can prove that there is a unique integer $R$ such that $R\times Q\equiv P(\mathrm{mod}998244353)$ and $0\le R<998244353$. Find this $R$.

Constraints

$2\le N\le 10^{18}$
$N$ is an integer.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print the probability, modulo $998244353$, that your integer ends up being $N$.

Sample Input 1

6

Sample Output 1

239578645

One of the possible procedures is as follows.
Initially, your integer is $1$.
You cast a die, and it shows $2$. Your integer becomes $1\times 2=2$.
You cast a die, and it shows $4$. Your integer becomes $2\times 4=8$.
Now your integer is not less than $6$, so you terminate the procedure.
Your integer ends up being $8$, which is not equal to $N=6$.
The probability that your integer ends up being $6$ is $\frac{7}{25}$. Since $239578645\times 25\equiv 7(\mathrm{mod}998244353)$, print $239578645$.

Sample Input 2

7

Sample Output 2

0

No matter what the die shows, your integer never ends up being $7$.

Sample Input 3

300

Sample Output 3

183676961

Sample Input 4

979552051200000000

Sample Output 4

812376310

---

题目大意

这道题的意思筛骰子，筛到每个数（即1-6）的概率均等，把所筛到的数相乘记作$T$，筛到$T=N$的概率是多少

---

思路

这道题可以想到DP，这里先给出一个简单的DP转移方程：
$$dp[x]=\frac{1}{5}\sum _{i=2}^{6}dp[i\times x]$$
证明：
$$\begin{array}{c}\begin{array}{rl}& dp[x]=\frac{1}{6}dp[1\times x]+\frac{1}{6}\sum _{i=2}^{6}dp[i\times x]\\ & dp[x]-\frac{1}{6}dp[1\times x]=\frac{1}{6}\sum _{i=2}^{6}dp[i\times x]\\ & \frac{5}{6}dp[x]=\frac{1}{6}\sum _{i=2}^{6}dp[i\times x]\\ & \frac{5}{6}dp[x]÷\frac{5}{6}=\frac{1}{6}\sum _{i=2}^{6}dp[i\times x]÷\frac{5}{6}\\ & dp[x]=\frac{1}{5}\sum _{i=2}^{6}dp[i\times x]\end{array}\end{array}$$

但是，由于N很大，所以这样直接做肯定会TLE！
所以，我们想一想，因为有些数是不能被乘出来的，所以我们考虑哪些数会被乘出来！

因为乘的数只能是$2,3,4,5,6$，所以其实就相当于只能是$2,3,5$的幂。
即：分解质因数后有且仅有$2,3,5$这三个数（数量没关系）

那么分别考虑：
若是2的幂：则只会有${\log }_{2}10^{18}$
若是3的幂：则只会有${\log }_{3}10^{18}$
若是5的幂：则只会有${\log }_{5}10^{18}$

所以最多只会有：${\log }_{2}10^{18}\times {\log }_{3}10^{18}\times {\log }_{5}10^{18}$

时间复杂度肯定是可以接受的！

由于要考虑边界情况，所以我们可以用记忆化搜索来写，写的会简单点。对于题目中的$R\times Q\equiv P(\mathrm{mod}998244353)$ and $0\le R<998244353$，由于模数是质数，所以直接用快速幂求就行！

最后，输出的答案即为$dp[1]$，由于我们相当于倒着转移的。

---

代码

#include 
#include 
#define int long long

using namespace std;

const int MOD = 998244353;

int n, IE5;
unordered_map<int, int> val;

inline int dp(int x)
{
	if (x > n) return 0;
	else if (x == n) return 1;
	else if (val.count((x))) return val[x];
	
	int res = 0;
	for (int i = 2; i <= 6; i ++) res += dp(i * x);
	
	res = res * IE5 % MOD;
	val[x] = res;
	
	return val[x]; 
}

int qmi(int a, int b)
{
	int res = 1;
	
	while (b)
	{
		if (b & 1) res = res * a % MOD;
		a = a * a % MOD;
		b >>= 1;
	}
	
	return res;
}

void init()
{
	IE5 = qmi(5, MOD - 2);
}

signed main()
{
	init();
	
	cin >> n;
	
	cout << dp(1) << endl;
}

F - More Holidays

原题

Problem Statement

You are given a string $S$ of length $N$ consisting of o and x, and integers $M$ and $K$.

$S$ is guaranteed to contain at least one x.
Let $T$ be the string of length $NM$ obtained by concatenating $M$ copies of $S$.
Consider replacing exactly $K$ x's in $T$ with o.

Your objective is to have as long a contiguous substring consisting of o as possible in the resulting $T$.

Find the maximum length of a contiguous substring consisting of o that you can obtain.

Constraints

$N$, $M$, and $K$ are integers.
$1\le N\le 3\times 10^5$
$1\le M\le 10^9$
$1\le K\le x$, where $x$ is the number of x's in the string $T$.
$S$ is a string of length $N$ consisting of o and x.
$S$ has at least one x.

Input

The input is given from Standard Input in the following format:

$N$ $M$ $K$
$S$

Output

Print the answer as an integer.

Sample Input 1

10 1 2
ooxxooooox

Sample Output 1

9

$S=$ ooxxooooox and $T=$ ooxxooooox.

Replacing x at the third and fourth characters with o makes $T=$ ooooooooox.

Now we have a length-$9$ contiguous substring consisting of o, which is the longest possible.

Sample Input 2

5 3 4
oxxox

Sample Output 2

8

$S=$ oxxox and $T=$ oxxoxoxxoxoxxox.

Replacing x at the $5,7,8$ and $10$-th characters with o makes $T=$ oxxooooooooxxox.

Now we have a length-$8$ contiguous substring consisting of o, which is the longest possible.

Sample Input 3

30 1000000000 9982443530
oxoxooxoxoxooxoxooxxxoxxxooxox

Sample Output 3

19964887064

题目大意

字符串S由x和o组成，长度是N，M表示一共M个字符串S连接组成一个新的S，K表示在新的S中修改K个x为o，问S中最长o相连的子串的长度。

---

思路

因为S是M个重复字符串（每个长度为N)组成，所以如果第一个要改变的x一定在前N个字符中，此时可以有两种方法来做这个题。

方法一：

硬算，比赛时我就是硬算的，结果算的不对，导致时间不足了。

方法二：

采用遍历加二分的方法来完成。
1、对原始的S做一次前缀和，计算去前i个字符中x的个数。
2、对原始的S反过来再计算一次前缀和，计算第i个字符后x的个数。
3、计算原始的S共有多少个x，设为p
4、如果K > p，那么 NM长度的新S中K / p 个原S中的x都要转为o，K % p的x就要从前面的第一个S和后面的S中截取。所以只需要计算从第一个S中的第i位开始截取，到后面S的哪一位结束就可以了。这个过程，可以用二分来完成。

注意：求x个数的公式一定要仔细推，很容易推错！

写的简略了点，有问题可以问我！

代码

#include 
#define int long long

using namespace std;

const int N = 3e5 + 10;

int n, m, k, p;
int frw[N], rvs[N];
string s;

bool check(int l, int r)
{
	int num_x = (r <= n) ? frw[r] - frw[l - 1] : rvs[l] + frw[r % n] + (r - n) / n * p;
	
	return num_x <= k;
}

signed main()
{
	cin >> n >> m >> k >> s;
	
	s = ' ' + s;
	for (int i = 1; i <= n; i ++)
		frw[i] = frw[i - 1] + (s[i] == 'x'), p += (s[i] == 'x');
		
	for (int i = n; i >= 1; i --)
		rvs[i] = rvs[i + 1] + (s[i] == 'x');
		
	int res = 0;
	for (int i = 1; i <= n; i ++)
	{
		int l = i, r = n * m;
		while (l < r)
		{
			int mid = l + r + 1 >> 1;
			if (check(i, mid)) l = mid;
			else r = mid - 1;
		}
		res = max(res, l - i + 1);
	}
	
	cout << res << endl;
}

G - P-smooth number

原题

Problem Statement

A positive integer is called a $k$-smooth number if none of its prime factors exceeds $k$.

Given an integer $N$ and a prime $P$ not exceeding $100$, find the number of $P$-smooth numbers not exceeding $N$.

Constraints

$N$ is an integer such that $1\le N\le 10^{16}$.
$P$ is a prime such that $2\le P\le 100$.

Input

The input is given from Standard Input in the following format:
$N$ $P$

Output

Print the answer as an integer.

Sample Input 1

36 3

Sample Output 1

14

The $3$-smooth numbers not exceeding $36$ are the following $14$ integers: $1,2,3,4,6,8,9,12,16,18,24,27,32,36$.

Note that $1$ is a $k$-smooth number for all primes $k$.

Sample Input 2

10000000000000000 97

Sample Output 2

2345134674

---

题目大意

计算N以内所有P的平滑数有多少个，其中P不超过100。
平滑数的定义：一个质因子不超过K的数，叫做K的平滑数。

---

思路

学习了一下官方的思路，这个题采用双向搜索（meet-in-the-middle trick），先从两端开始搜索，然后将结果放入两个集合中，最后将两个集合的混合计算。

注意：1是一个特殊的，永远是平滑数！

写的简略了点，有问题可以问我！

---

代码

#include 
#include 
#include 
#define int long long

using namespace std;

int n, p;

void push(vector<int> &a, int num)
{
	int sz = a.size();
	for (int i = 0; i < sz; i ++)
	{
		int t = a[i];
		while (1)
		{
			t *= num;
			if (t > n) break;
			a.push_back(t);
		}
	}
}

signed main()
{
	vector<int> prime = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};
	
	cin >> n >> p;
	
	while (p < prime.back()) prime.pop_back();
	
	vector<int> frt = {1}, bck = {1};
	for (auto &c : prime)
		if (frt.size() < bck.size()) push(frt, c);
		else push(bck, c);
		
	sort(frt.begin(), frt.end());
	sort(bck.begin(), bck.end());
	
	int res = 0;
	for (int i = 0, j = bck.size() - 1; i < frt.size(); i ++)
	{
		int left = n / frt[i];
		while (j >= 0 && left < bck[j]) j --;
		if (j < 0) break;
		res += j + 1;
	}
	
	cout << res << endl;
}

本次题解的E题得到了国家队大佬刘一平老师的指点，感谢刘老师。

因为最近感冒，所以拖到现在才更新。

今天就到这里了！

大家有什么问题尽管提，我都会尽力回答的！

吾欲您伸手，点的小赞赞。吾欲您喜欢，点得小关注！