KNN算法
文章目录
- 什么是KNN算法
- 欧式距离
- 曼哈顿距离
- 切比雪夫距离
- 闵可夫斯基距离
- KNN算法流程
- K值选择
- K值选择对模型的影响
- sklearn代码实现
- sklearn的优势
- KNN项目应用
什么是KNN算法
K Nearest Neighbor算法⼜叫KNN算法,这个算法是机器学习⾥⾯⼀个⽐较经典的算法。
如果⼀个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的⼤多数属于某⼀个类别,则该样本也属于这个类别。
欧式距离
在机器学习过程中,对于函数 dist(),若它是⼀"距离度量" (distance measure),则需满⾜⼀些基本性质:
欧⽒距离(Euclidean Distance)是最容易直观理解的距离度量⽅法,我们小学、初中和⾼中接触到的两个点在空间中的距离⼀般都是指欧⽒距离。
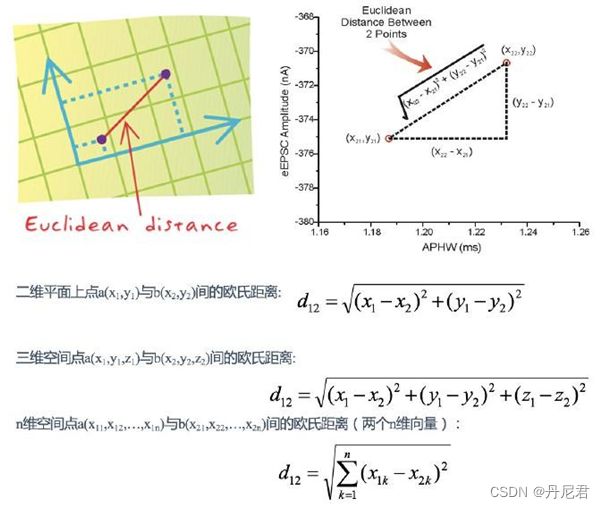
曼哈顿距离
在曼哈顿街区要从⼀个⼗字路⼝开⻋到另⼀个⼗字路⼝,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离(Manhattan Distance)”。曼哈顿距离也称为“城市街区距离”(City Block distance)

切比雪夫距离
国际象棋中,国王可以直⾏、横⾏、斜⾏,所以国王⾛⼀步可以移动到相邻8个⽅
格中的任意⼀个。国王从格⼦(x1,y1)⾛到格⼦(x2,y2)最少需要多少步?这个距离就叫切⽐雪夫距离(Chebyshev Distance)。

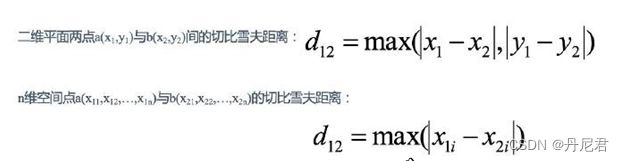
闵可夫斯基距离
闵⽒距离(Minkowski Distance)不是⼀种距离,⽽是⼀组距离的定义,是对多个距
离度量公式的概括性的表述。
两个n维变量a(x ,x ,…,x )与b(x ,x ,…,x )间的闵可夫斯基距离定义为:

其中p是⼀个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧⽒距离;
当p→∞时,就是切⽐雪夫距离。
根据p的不同,闵⽒距离可以表示某⼀类/种的距离。
KNN算法流程
1)计算已知类别数据集中的点与当前点之间的距离
2)按距离递增次序排序
3)选取与当前点距离最⼩的k个点
4)统计前k个点所在的类别出现的频率
5)返回前k个点出现频率最⾼的类别作为当前点的预测分类
K值选择
- 选择较⼩的K值,就相当于⽤较⼩的领域中的训练实例进⾏预测,
“学习”近似误差会减⼩,只有与输⼊实例较近或相似的训练实例才会对预
测结果起作⽤,与此同时带来的问题是“学习”的估计误差会增⼤,
换句话说,K值的减⼩就意味着整体模型变得复杂,容易发⽣过拟合; - 选择较⼤的K值,就相当于⽤较⼤领域中的训练实例进⾏预测,
其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增⼤。这
时候,与输⼊实例较远(不相似的)训练实例也会对预测器作⽤,使预测
发⽣错误。
且K值的增⼤就意味着整体的模型变得简单。 - K=N(N为训练样本个数),则完全不⾜取,
因为此时⽆论输⼊实例是什么,都只是简单的预测它属于在训练实例中最
多的类,模型过于简单,忽略了训练实例中⼤量有⽤信息。
在实际应⽤中,K值⼀般取⼀个⽐较⼩的数值,例如采⽤交叉验证法(简单来
说,就是把训练数据在分成两组:训练集和验证集)来选择最优的K值。
K值选择对模型的影响
K值过⼩:
容易受到异常点的影响
容易过拟合
k值过⼤:
受到样本均衡的问题
容易⽋拟合
sklearn代码实现
# 导⼊模块
from sklearn.neighbors import KNeighborsClassifier
# 构造数据集
x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
x = [[39,0,31],[3,2,65],[2,3,55],[9,38,2],[8,34,17],[5,2,57],[21,17,5],[45,2,9
y = [0,1,2,2,2,2,1,1]
# 模型训练
estimator = KNeighborsClassifier(n_neighbors=1)
# 使⽤fit⽅法进⾏训练
estimator.fit(x, y)
estimator.predict([[1]])
# 数据集格式⼆对应的测试数据
# estimator.predict([[23,3,17]])
sklearn的优势
- ⽂档多,且规范
- 包含的算法多
- 实现起来容易
KNN项目应用
如果需要本文完整代码,以上数据资源的小伙伴可以私信我哦!