使用扩展卡尔曼滤波（EKF）融合激光雷达和雷达数据（Matlab代码实现）

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

---

1 概述

大多数自动驾驶汽车都配备了激光雷达和雷达。然而，这两者的输出是不同的，激光雷达的输出是笛卡尔坐标中物体的位置，而雷达给出物体在极坐标中的位置和速度。使用扩展卡尔曼滤波器是因为它可以融合非线性数据，在这种情况下是来自笛卡尔坐标和极坐标的数据。为了估计非线性测量，引入了雅可比矩阵。

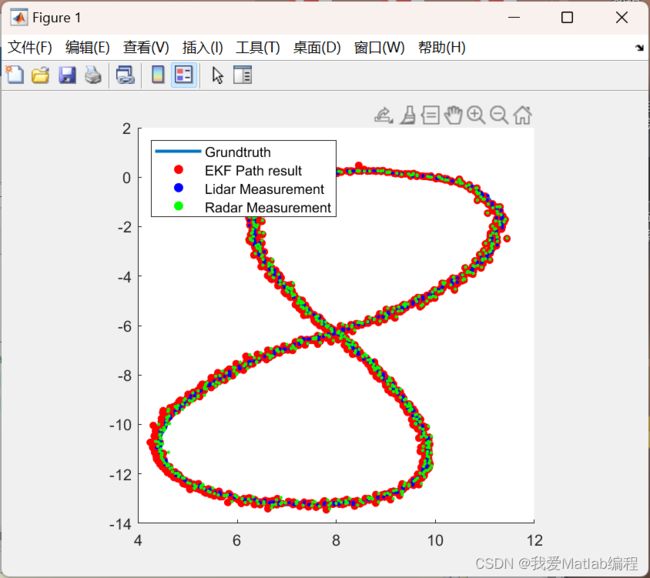
2 运行结果

主函数部分代码：

clear;
clf;
dt = 0.1;
Data = csvread('Radar_Lidar_Data1.csv',1,1);
% Data = csvread('Radar_Lidar_Data2.csv',1,1);
Radar_Measurement = [];
Lidar_Measurement = [];
EKF_Path = [];


F = [[1, 0, dt, 0];
     [0, 1, 0, dt];
     [0, 0, 1, 0];
     [0, 0, 0, 1]];
 
u = 0;
B = [(dt^2)/2 (dt^2)/2 dt dt]';


P = [[1, 0, 0, 0];
     [0, 1, 0, 0];
     [0, 0, 1000, 0];
     [0, 0, 0, 1000]];




R_l = [[0.0025, 0];
       [0, 0.0025]];
  
R_r = [[0.09, 0, 0];
      [0, 0.005, 0];
      [0, 0, 0.09]];
 


Q = [(dt^2)/4 0 (dt^3)/2 0;
     0 (dt^2)/4 0 (dt^3)/2;
     (dt^3/2) 0 (dt^2) 0;
     0 (dt^3)/2 0 (dt^2)];




H = [[1, 0, 0, 0];
     [0, 1, 0, 0]];


I = eye(4);


if (Data(1,1) == 1)
    x = [Data(1,2); Data(1,3); 0; 0];
else
    x = [Data(1,2); Data(1,3); Data(1,4); 0];
end


for n = 1:length(Data)
    
    if (Data(n,1) == 2)
        
        %prediction
        x = F * x + B*u;
        P = F * P * transpose(F) + Q;


        %measurement update
        Z = Data(n,2:4);
        X = Z(1)*cos(Z(2));
        Y = Z(1)*sin(Z(2));
        VX = Z(3)*cos(Z(2));
        VY = Z(3)*sin(Z(2));


        c1 = X^2 + Y^2;
        c2 = sqrt(c1);
        c3 = c1 * c2;
        if (c1==0 || c2==0 || c3==0)
            H_Jac = [[0, 0, 0, 0];
                     [0, 0, 0, 0];
                     [0, 0, 0, 0]];
        else
            H_Jac = [[X/c2, Y/c2, 0, 0];
                    [-Y/c1, X/c1, 0, 0];
                    [(Y*(VX*Y-VY*X))/c3, (X*(X*VY-Y*VX))/c3, X/c2, Y/c2]];
        end
        Z_Car = [X; Y; VX; VY];
        y = transpose(Z) - (H_Jac * Z_Car);
        S = H_Jac * P * transpose(H_Jac) + R_r;
        K = P * transpose(H_Jac) * inv(S);
        x = Z_Car + (K * y);
        P = (I - (K * H_Jac)) * P;
        EKF_Path = [EKF_Path;[x(1),x(2)]];
        Radar_Measurement = [Radar_Measurement; Data(n,2:4)];
    
    else
        
        %prediction
        x = (F * x) + B*u;
        P = F * P * transpose(F) + Q;


        %measurement update
        Z = Data(n,2:3);
        y = transpose(Z) - (H * x);
        S = H * P * transpose(H) + R_l;
        K = P * transpose(H) * inv(S);
        x = x + (K * y);
        P = (I - (K * H)) * P;
        EKF_Path = [EKF_Path;[x(1),x(2)]];
        Lidar_Measurement = [Lidar_Measurement; Data(n,2:3)];
    end
    
end

3 参考文献

[1]杨春玲,倪晋麟,刘国岁,郑全战.转换坐标卡尔曼滤波器的雷达目标跟踪[J].电子学报,1999(03):121-123.

部分理论引用网络文献，若有侵权联系博主删除。

4 Matlab代码实现