数据结构——串（字符串）

一 串的定义和实现

1 定义

串是由零个或多个字符组成的有限序列，可以是字母，数字或者其他字符

由一个或多个空格组成的串称为空格串（空格也是一种符号）

如“hello world 232@#%^&”

2 串的存储结构

2.1 定长顺序存储表示

#define maxline 255
typedef struct
{
    char ch[maxline];
    int length;
}Sstring;

一组连续的存储单元

超过的长度会发生截断；一般字符串的结尾都有一个隐含的“\0”，不计入长度

2.2 堆分配存储表示

仍是一组连续的存储单元，但是存储空间是执行过程中动态分配的

typedef struct
{
    char *ch;
    int length;
}Hstring;

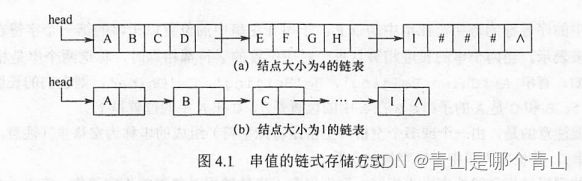
2.3 块链存储表示

每个结点可以存放一个字符，也可以存放多个字符

每个结点称为块，整个链表称为块链结构

最后一个结点占不满时通常用#补上

3 串的基本操作

Strassign(&T,chars);            \\T赋值到chars
Strcopy(&T,S);                  \\S复制到T
Strempty(S);                    \\判空
Strcompare(S,T);                \\比较ST，S>T返回值大于0
Strlength(S);                   \\求串长
Substring(&Sub,S,pos,len);      \\用sub返回s从pos位置长度为len的子串
Concat(&T,S1,S2);               \\T返回s1和s2的串接
Index(S,T);                     \\若S中存在T相同的子串，返回第一次出现的位置，否则为0
Clearstring(&S);                \\清空
Destroystring(&S);              \\销毁

二 串的模式匹配

1 简单的模式匹配算法

模式匹配：子串的定位操作，求的是子串在主串中的位置

采用定长顺序存储结构

暴力算法：

int Index(Sstring S,Sstring R)
{
    int i =1,j=1;
    while(i<=S.length && j<= T.length)
    {
        if(S.ch[i]==T.ch[j])
        {
            i++;
            j++;
        }
        else
        {
            i=i-j+2;           \\比对失败倒退下标
            j=1;
        }
    }
    if(j >T.length)
        return i-T.length;     \\找到了位置并返回
    else
        return 0;              \\没找到
}

时间复杂段：O(mn)，m，n分别是子串和主串的长度

算法思想：主串和子串的字符一一对比，如果不对，子串倒退到一开始，主串倒退到刚刚比较的的下一个位置

当子串为“00001”，主串为“0000000000000000000000001”时，可以预想到查找效率极低，需要匹配到最后一个位置才能找到

2 串的模式匹配算法——KMP算法

从刚刚的例子可以看出第四次和第五次是不需要进行的，因为从第三次的结果可以看出“b” “c” “a”是无需进行比较的，仅需向右滑动三个位置

如果已匹配相等的前缀序列中有某个后缀正好是子串的前缀，那么就可以将子串向后滑动到与这些相等字符对齐的位置

2.1 字符串的前缀，后缀和部分匹配值

前缀：除最后一个字符意外，字符串的所有头部子串

后缀：除第一个字符外，字符串的所有尾部子串

部分匹配值：字符串的前缀和后缀的最长相等前后缀长度，以下记为PM

‘a’：前后缀为空，PM=0

‘ab’：前缀‘a’，后缀‘b’，‘a’$\bigcap$‘b’=$\varnothing$，PM=0

‘aba’，前缀‘a，ab’，后缀‘a，ba’，并集为‘a’，PM=1

‘abab’，前缀‘a，ab，aba’，后缀‘b，ab，bab’，并集‘ab’，PM=2

‘ababa’，前缀‘a，ab，aba，abab’，后缀‘a，ba，aba，baba’，并集‘a，aba’，PM=3

所以‘ababa’的部分匹配值为00123

那么刚刚例子中abcac的PM就为

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	0	0	1	0

采用PM的移动算法：

移动位数 = 已匹配的字符数 - 最后一个匹配成功的字符对应的PM

主串没有回退，时间复杂度：O(n+m)，大大提高了效率

2.2 KMP算法的原理

通过上述的部分匹配值可以得出匹配失败时主串对比的移动位数

写成式子：move=(j-1)-PM[j-1]

但是失败时总是去找匹配失败的上一个PM值，使用起来不太方便，所有将所有PM表右移一位，得到next数组：

编号	1	2	3	4	5
S	a	b	c	a	c
PM	-1	0	0	0	1

第一个元素右移后用-1来填充，因为若是第一个元素匹配失败，只需要将子串向右移动一位再比较，不需要计算子串移动的位数

最后一个元素溢出，但上一个PM本来就是计算下一个元素的，所有这个PM不存在下一个元素，可以舍弃

移动位数：move = (j-1) - next[j]

所以指针J回退的位置：j=j-move=next[j]+1

为了再使得公式简单简洁，再把next数组整体+1

编号	1	2	3	4	5
S	a	b	c	a	c
PM	0	1	1	1	2

最终的子串指针变化公式j=next[j]

next[j]的含义：在子串的第j个字符与主串发生失配时，则跳到子串的next[j]位置重新与主串当前位置进行比较

怎么推理next数组的一般公式？

假设主串为S₁S₂……S_n，模式串为p₁p₂……p_m，当主串的第i个字符与模式串的第j个字符失配，子串应向右滑动多远，然后与模式串的那个字符比较？

假设此时应该与第k（k,>k满足下列条件

​ ‘p₁p₂……p_k-1’=‘ p_j-k+1p_j-k+2……p_j-1’

（1）若满足上述条件，失配时，将模式向右滑动至模式中第k个字符和主串第i个字符对齐，此时模式中前k-1个字符的子串必定与主串中第i个字符之前长度为k-1的子串相等，只需从模式第k个字符与主串第i个字符继续比较即可

（2）不满足上述条件时（k=1），直接将模式串右移j-1位，让主串的第i个字符与模式串第一个字符对比，此时右移位数最大

（3）若模式串的第一个子串就与主串的第i个字符失配时，规定next[1]=0；模式串右移一位，从主串的下一个位置i+1与模式串的第一个位置继续对比

即next函数的公式为

首先可知next[1]=0，next[j]=k；那next[j+1]为多少呢，有两种情况：

（1）若p_k=p_j，则满足条件 ‘p₁p₂……p_k-1’=‘ p_j-k+1p_j-k+2……p_j-1’ ，所以next[j+1]=k+1，即next[j+1]=next[j]+1

（2）若p_k$\ne$p_j，不满足上述条件，则把p₁…p_k向右滑动到next[k]与p_j比较，若p_next[k]与p_j还是不匹配，继续找更短的相等前后缀，继续用p_{next[next[k]]}比较，直到更小的k’满足条件，next[j+1]=k’+1；如果不存在k，则令next[j+1]=1

举例说明：

j	1	2	3	4	5	6	7	8	9
模式	a	b	a	a	b	c	a	b	a
next[j]	0	1	1	2	2	3	1	2	3

j=1：初始next[1]=0

j=2：往前不存在p₀与p₁相等，则next[2]=1

j=3：往前不存在p与p₂相等，则next[3]=1

j=4：通过p₃的next判断p_next[3]即p₁=p₃，则next[4]=next[3]+1=2，同时也是next[4]=k+1=2

j=5：通过p_{next[next[4]]}即p₁=p₄，则k=next[next[4]]=1，next[5]=k+1=2

j=6：p₅=p_next[2]，则k=2，next[6]=k+1=3

j=7：不存在p与p₆相等，则next[7]=1

j=8：p₇=p₁，则k=1，next[8]=1+1=2

j=9：p₈=p₂，则k=2，next[9]=2+1=3

代码如下

void getnext(Sstring T,int next[])
{
    int i =1,j=0;
    next[1]=0;
    while(iT.length)
    {
        return i-T.length;
    }
    else
    {
        return 0;
    }
}

2.3 KMP算法的优化

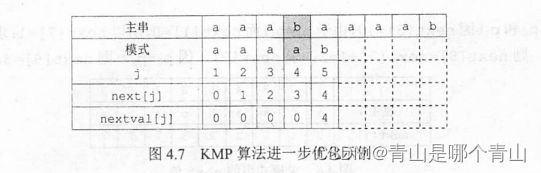
前面的next数组仍有缺项，比如‘aaaab ’和‘aaabaaaab’ 匹配时

不应该出现p_j=p_next[j]，当p_j$\ne$s_j时，下次匹配必然还是p_next[j]与s_j比较，毫无意义

如果出现p_j=p_next[j]，需要再次递归，将next[j]修正为next[next[j]]，直到不相等，新数组命名为nextval

void getnextval(Sstring T,int nextval[])
{
    int i =1,j=0;
    nextval[1]=0;
    while(i