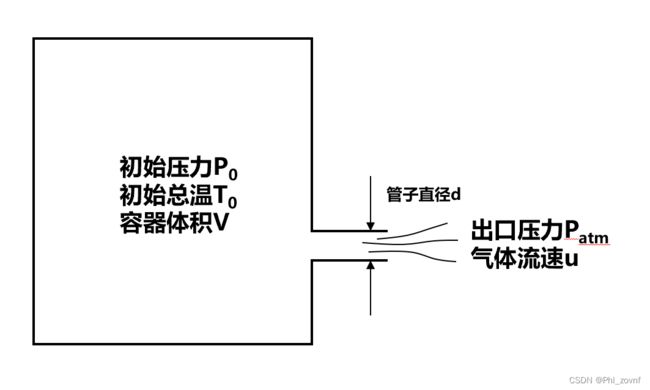
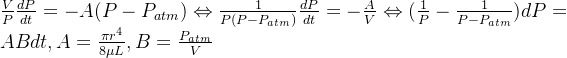恒容容器放气的瞬时流量的计算
有时候,你会遇到一个问题,该问题的描述如下:
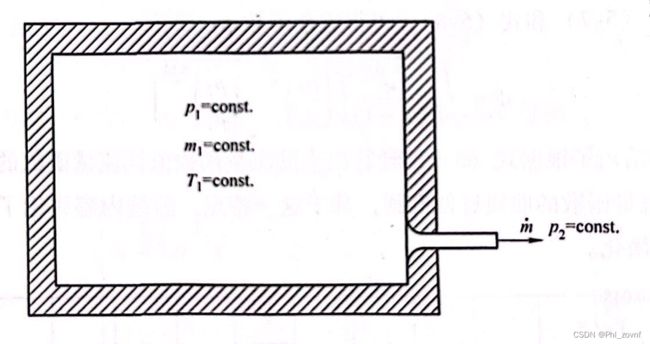
你有一个已知体积的容器,设容器体积为
,里面装有一定压力(初始压力)的气体,如空气或氢气等,设初始压力为
,容器出口连接着一个阀门开关,开关后面接直径为
的钢管,钢管出口为一个大气压
。当阀门瞬间全开时,气体出口的瞬时流量值随时间变化到底是怎么样的呢?
该问题相当于已知气体管道直径
,即已知管道横截面积
,已知气体管道两端的气压差
,同时知道进口气体总温
为323K,求出口瞬时质量流量
或瞬时体积流量
随时间
的变化关系和曲线,其中
是气体密度,
为出口气体流速,
即为气体流过管道的横截面积。
1. 第一种方法:根据哈根泊谡叶方程
利用理想气体方程:![]() (假设放气是等温过程,
(假设放气是等温过程,![]() )和哈根泊谡叶关系式:
)和哈根泊谡叶关系式:![]() ,
,![]() 表示的是体积流量,单位为
表示的是体积流量,单位为![]() ,
,![]() 是管子的半径,
是管子的半径,![]() 是流体的动力黏度,单位是
是流体的动力黏度,单位是![]() ,
,![]() 是管子的长度,压强
是管子的长度,压强![]() 的单位为
的单位为![]() 。两个方程联立,
。两个方程联立,
![]() ,考虑等温过程,有
,考虑等温过程,有![]() ,也就是说,
,也就是说,![]() 的变化仅与容器内压力的变化有关。进一步,根据
的变化仅与容器内压力的变化有关。进一步,根据![]() ,假设密度
,假设密度![]() 不变,有:
不变,有:![]() ,积分后得到:
,积分后得到:![]() ,有
,有![]() ,利用该关系式,得到
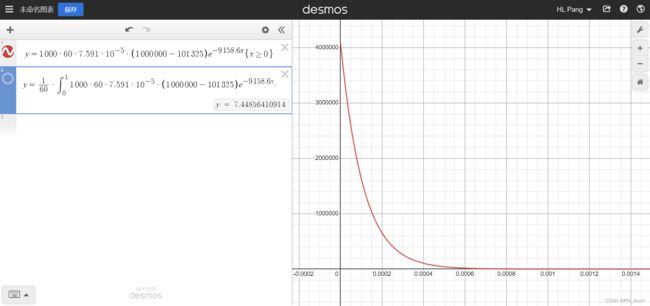
,利用该关系式,得到![]() 随时间
随时间![]() 的关系如下图所示,为一指数函数形式,而且可以通过积分,得到积分总流量为
的关系如下图所示,为一指数函数形式,而且可以通过积分,得到积分总流量为![]() ,根据
,根据![]() ,可见积分与差分得出的总流量非常接近。
,可见积分与差分得出的总流量非常接近。
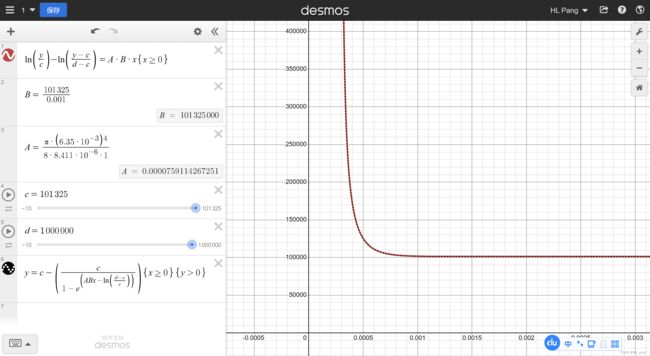
若气体密度![]() 不是常数,则根据
不是常数,则根据![]() ,有
,有![]() ,进一步有:
,进一步有:
通过数值计算,时间小量取![]() ,得到的质量流量曲线如下图,积分得到总流过的质量为
,得到的质量流量曲线如下图,积分得到总流过的质量为![]() ,与
,与![]() 有差异,这是因为时间小量
有差异,这是因为时间小量![]() 不够小导致的,当你取
不够小导致的,当你取![]() 时,积分得到总流过的质量为
时,积分得到总流过的质量为![]() ,此时就已经与
,此时就已经与![]() 非常接近了。
非常接近了。
 以密度
以密度![]() 不变的解法为例,一开始的瞬时流量值非常离谱,可以去到
不变的解法为例,一开始的瞬时流量值非常离谱,可以去到![]() ,根据
,根据![]() ,
,![]() 可以知道出口流体平均速度
可以知道出口流体平均速度![]() ,光速是
,光速是![]() ,出口速度已经达到
,出口速度已经达到![]() 倍的光速,也超过空气声速
倍的光速,也超过空气声速![]() ,妥妥是一个超音速流,而且放气过程时间非常短,不超过
,妥妥是一个超音速流,而且放气过程时间非常短,不超过![]() 。经过大量的资料查询,该结果似乎与实际测试不符。
。经过大量的资料查询,该结果似乎与实际测试不符。
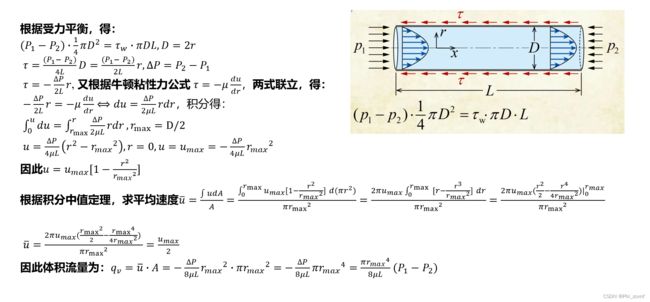
附:关于哈根泊谡叶关系式的推导,见下图。
2. 第二种方法:根据气体动力学推算
为什么第一种方法就不符合实际呢?前人发现,收缩的出口在气流流速加速到马赫数1时,即
时,气体流速达到上限。
假设排气过程与气体管道壁面的换热忽略不计,即壁面是绝热的,气体流体是一个准稳态问题,排气口相当于是收缩,没有扩张,根据气体动力学可知,出口气体流速只能加速到1马赫数,即![]() 。根据总静温关系式
。根据总静温关系式![]() ,得知
,得知![]() 。再根据马赫数定义式
。再根据马赫数定义式![]() ,这里
,这里![]() 是气体比热容比,定义为定压比热
是气体比热容比,定义为定压比热![]() 与定容比热
与定容比热![]() 之比,变换后有
之比,变换后有![]() ,
,![]() ,
,![]() ,比气体常数
,比气体常数![]() 为:
为:![]() ,得到氢气气体流速
,得到氢气气体流速![]() 。
。
根据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为一个大气压。在
为一个大气压。在![]() 的壅塞流阶段,可解得
的壅塞流阶段,可解得![]() 。这阶段,理解为流速
。这阶段,理解为流速![]() 不变,
不变,![]() 变化导致的
变化导致的![]() 变化,瞬时质量流量也会随之变化,但体积流量
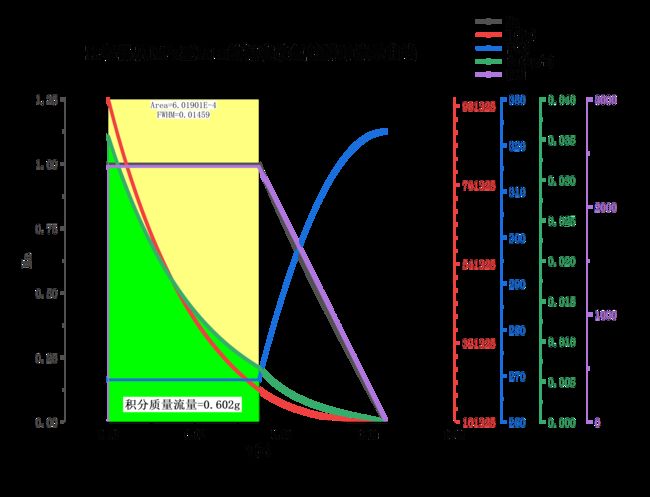
变化,瞬时质量流量也会随之变化,但体积流量![]() 不变。如下图所示,绿色曲线是瞬时流量,紫色曲线是体积流量,绿色部分面积是积分得到的总质量流量,通过积分得到壅塞流下的总质量流量为
不变。如下图所示,绿色曲线是瞬时流量,紫色曲线是体积流量,绿色部分面积是积分得到的总质量流量,通过积分得到壅塞流下的总质量流量为![]() ,换算成密度为
,换算成密度为![]() 的体积流量为
的体积流量为![]() 。
。
后面非壅塞流状态下的亚声速流,原则上也是利用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,这5个式子得到
,这5个式子得到![]() 的关系,我用欧拉法获得解析解的近似值,得到后续的流量曲线,具体步骤是,知道压力初始条件
的关系,我用欧拉法获得解析解的近似值,得到后续的流量曲线,具体步骤是,知道压力初始条件![]() ,初始瞬时流量为
,初始瞬时流量为![]() ,也就是等于壅塞流状态下最后一刻时间的流量,然后利用瞬时流量乘以时间小量,得到
,也就是等于壅塞流状态下最后一刻时间的流量,然后利用瞬时流量乘以时间小量,得到![]() ,再利用关系式
,再利用关系式![]() ,得到
,得到![]() 的变化量,然后计算马赫数
的变化量,然后计算马赫数![]() 、速度
、速度![]() ,温度
,温度![]() 等参数,不断进行迭代计算,当
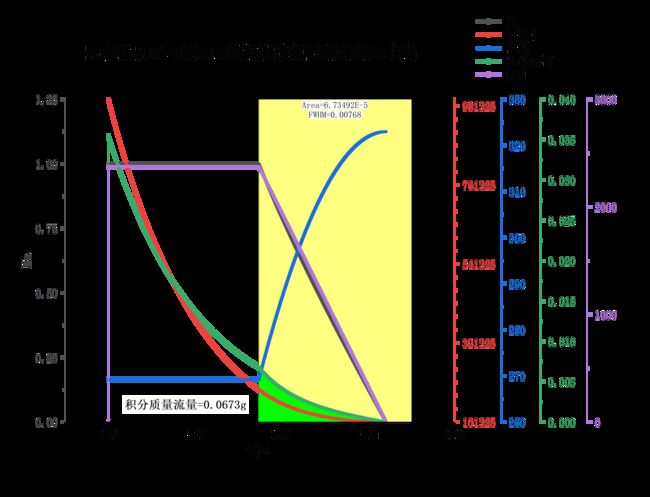
等参数,不断进行迭代计算,当![]() 时结束迭代。如下图中绿色的质量流量曲线和紫色的体积流量曲线,通过积分面积算得亚声速流下总质量流量为
时结束迭代。如下图中绿色的质量流量曲线和紫色的体积流量曲线,通过积分面积算得亚声速流下总质量流量为![]() ,换算成密度为
,换算成密度为![]() 的体积流量为
的体积流量为![]() ,因此放氢整个过程总质量流量为
,因此放氢整个过程总质量流量为![]() ,与
,与![]() 算出来的基本一致。整个过程的总体积流量为
算出来的基本一致。整个过程的总体积流量为![]() 。
。
3. 第三种方法:绝热小孔自由放气模型
根据伯努利方程得到气体的能量方程![]() ,根据能量守恒定律,将上述方程应用于小孔,得到小孔上游和下游状态参数的关系:
,根据能量守恒定律,将上述方程应用于小孔,得到小孔上游和下游状态参数的关系:![]() ,容腔内气体近似保持静止,即小孔上游速度
,容腔内气体近似保持静止,即小孔上游速度![]() 。根据焓值的定义,上式可变为
。根据焓值的定义,上式可变为![]() ,其中
,其中![]() 为气体的恒压热容,
为气体的恒压热容,![]() 为上游热力学温度,
为上游热力学温度,![]() 为下游热力学温度。
为下游热力学温度。
由于气流流经小孔时,与管壁接触面小,流动快,可近似认为气体流动过程是绝热过程。将绝热方程式![]() ,
,![]() ,
,![]() ,
,![]() 是比热容比,
是比热容比,![]() 是定压热容,
是定压热容,![]() 是定容热容,以及将
是定容热容,以及将![]() 代入方程
代入方程![]() ,可得
,可得![]() ,根据理想气体方程式
,根据理想气体方程式![]() ,可得到以下关系:
,可得到以下关系:
![]()
根据质量流量的定义,有![]() ,这里由于计算的是小孔的气体流速,因此密度
,这里由于计算的是小孔的气体流速,因此密度![]() ,速度即为
,速度即为![]() ,
,![]() 为气体流过小孔管的横截面积。将绝热关系式
为气体流过小孔管的横截面积。将绝热关系式![]() ,和
,和![]() 代入质量流量定义式,首先有
代入质量流量定义式,首先有![]() ,
,![]() ,因此有
,因此有![]() ,所以有
,所以有![]() ,化简有:
,化简有:
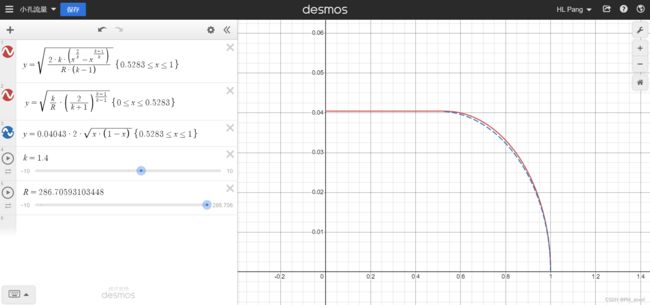
![]() ,定义流量函数
,定义流量函数![]() ,则有:
,则有:![]() ,将
,将![]() 看成自变量,
看成自变量,![]() 是因变量,研究
是因变量,研究 ![]() 随
随![]() 的变化曲线,有以下图形关系:
的变化曲线,有以下图形关系:
当![]() ,
,![]() ,进一步,选取
,进一步,选取![]() ,可以计算得到此时
,可以计算得到此时![]() 。将
。将![]() 代入
代入![]() ,可化简为:
,可化简为:,
![]() 。
。
根据《气动系统的基础与计算特性》一书所述,雷诺首先对上述 ![]() 时,
时,![]() 获得极值的物理现象,解释为:当马赫数等于1的状态时,气流处于声速,下游的气流信息不能向上传递,上游的气流状态不随下游压力的变化而变化,许多学者称该现象为壅塞状态。
获得极值的物理现象,解释为:当马赫数等于1的状态时,气流处于声速,下游的气流信息不能向上传递,上游的气流状态不随下游压力的变化而变化,许多学者称该现象为壅塞状态。![]() 被称为临界压力比,小于此值时,流量达到饱和,也可称为声速流。因此有如下式子,其图形如下图红实线所示。
被称为临界压力比,小于此值时,流量达到饱和,也可称为声速流。因此有如下式子,其图形如下图红实线所示。
工程上,经常用![]() 来代替
来代替![]() ,曲线如下图的蓝色虚线所示,从图形上看,两者曲线基本吻合,且当
,曲线如下图的蓝色虚线所示,从图形上看,两者曲线基本吻合,且当![]() 时,
时,![]() ,因此
,因此![]() 。两者曲线如下图所示,两者最大误差为3%。
。两者曲线如下图所示,两者最大误差为3%。
这样得到小孔的一维等熵流动的质量流量的近似公式:
![]()
,有
也就是说,壅塞状态下(声速流)质量流量曲线是指数形式下降的。亚声速流下的质量流量计算则比较复杂,根据状态方程的微分形式,并按绝热过程处理,有以下公式:
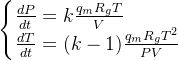 ,其中将质量流量公式
,其中将质量流量公式![]() 代入,使用差分形式,取时间微小量为
代入,使用差分形式,取时间微小量为![]() ,取
,取![]() ,
,![]() ,取
,取![]() ,
,![]() ,
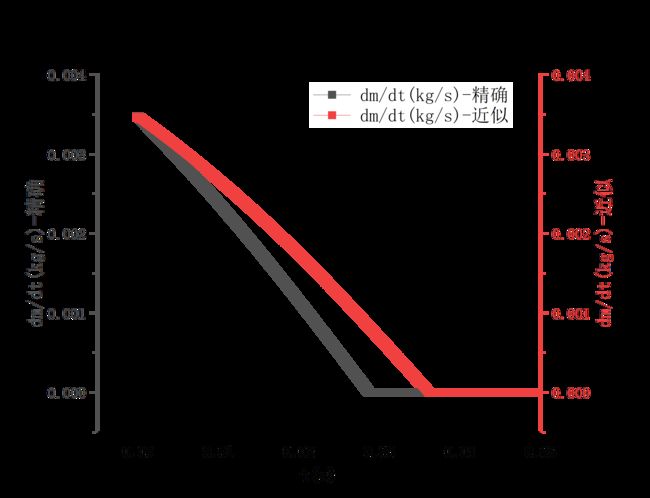
,![]() ,并进行数值计算,得到的质量流量曲线初看真的很像一条直线,但细看还是有点往上凸的。数值计算结果表明,亚声速流时间约为0.0287s,气体从初始323K降低至最后的269.17K。
,并进行数值计算,得到的质量流量曲线初看真的很像一条直线,但细看还是有点往上凸的。数值计算结果表明,亚声速流时间约为0.0287s,气体从初始323K降低至最后的269.17K。
若按简化后公式![]() ,这里
,这里![]() ,所以有
,所以有![]() ,根据此式计算质量流量,同样进行数值计算,亚声速流时间约为0.0361s,气体从初始323K降低至最后的257.32K。两者曲线偏差还不小。
,根据此式计算质量流量,同样进行数值计算,亚声速流时间约为0.0361s,气体从初始323K降低至最后的257.32K。两者曲线偏差还不小。
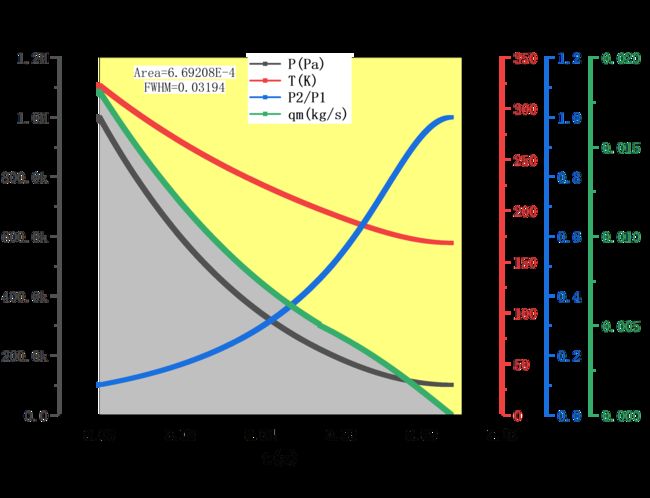
下面是压力、温度、压力比、质量流量随时间的变化曲线,该图计算过程如下,先知道初始各状态,如初始压力![]() ,初始温度
,初始温度![]() ,初始压力比
,初始压力比![]() 。用流量公式
。用流量公式![]() ,计算当前时刻的质量流量
,计算当前时刻的质量流量![]() ,将
,将![]() 乘以时间小量
乘以时间小量![]() ,得到
,得到![]() ,再用理想气体方程
,再用理想气体方程![]() 计算出
计算出![]() ,
,![]() 取当前时刻温度。由于这里当成是绝热放气过程,因此容器内气体温度也会变化,按公式
取当前时刻温度。由于这里当成是绝热放气过程,因此容器内气体温度也会变化,按公式![]() 的差分形式,将上述计算好的
的差分形式,将上述计算好的![]() ,当前温度
,当前温度![]() ,当前压力
,当前压力![]() ,代入后获得温度变化量
,代入后获得温度变化量![]() ,放气是对外界做功,因此气体温度下降。用当前压力减去
,放气是对外界做功,因此气体温度下降。用当前压力减去![]() ,获得下一时刻压力
,获得下一时刻压力![]() ;同理,获得下一刻温度
;同理,获得下一刻温度![]() 。这样,壅塞(声速)状态下,各物理量的曲线就出来了。当压力比
。这样,壅塞(声速)状态下,各物理量的曲线就出来了。当压力比![]() 时,变为亚声速流,此式流量公式变为
时,变为亚声速流,此式流量公式变为![]() ,按同样的数值计算方法,获得亚声速流下的各物理量随时间的变化曲线。
,按同样的数值计算方法,获得亚声速流下的各物理量随时间的变化曲线。
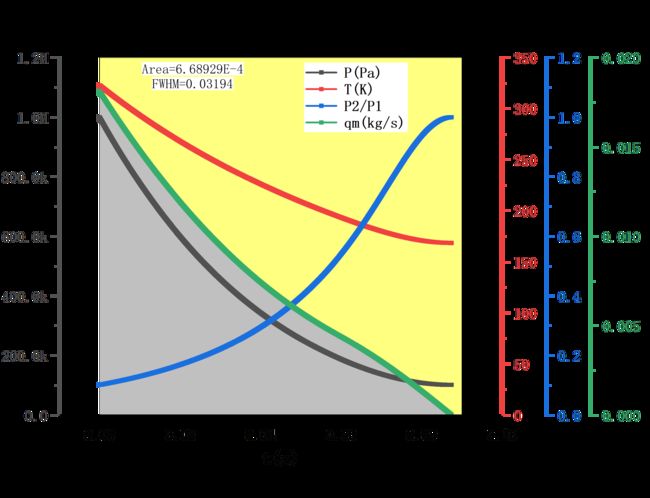
从曲线可以看出,压力曲线是类似指数型下降的,温度指数型下降,压力比有点类似S型曲线,质量流量在声速阶段是一下凹的曲线,亚声速是上凸的曲线,图中中间连接点不太连续的情况是因为数值计算中,受时间小量的限制,计算到临界压力比时,并不会恰好等于0.5283,压力变化会有个台阶,显得不是那么“连续”。
另外,整个放气过程时间为![]() ,对质量流量曲线进行积分,可以知道总流过的质量为
,对质量流量曲线进行积分,可以知道总流过的质量为![]() ,即
,即![]() ,与
,与![]() 算出来的还是一样。
算出来的还是一样。
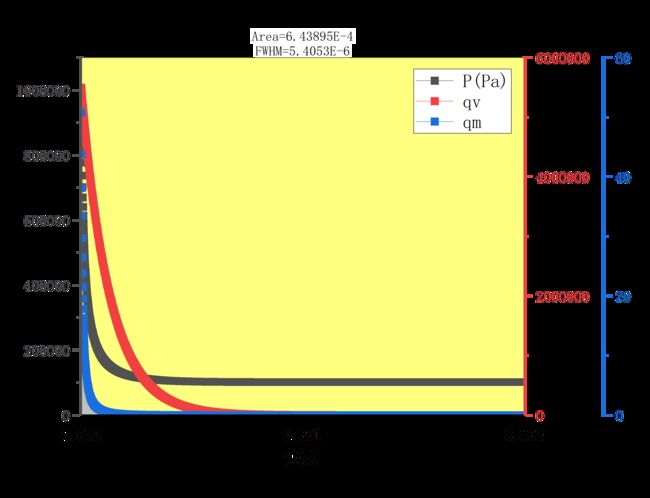
当然,压力差也可以完全用绝热公式 ![]() 计算,得到的曲线如下图,好像更丝滑一些,整个放气过程时间为
计算,得到的曲线如下图,好像更丝滑一些,整个放气过程时间为![]() ,积分算出总流过的质量仍为
,积分算出总流过的质量仍为![]() ,即
,即![]() 。
。
这是《气动系统的基础特性与计算》一书中的“容腔充放气”的曲线图, 其中各物理量进行了无量纲化(无因次响应)。从图中可以看出,流量曲线和压力曲线跟上述推导和计算过程基本类似,唯一区别是,温度曲线它是会回升的,这是因为书本中考虑了放气过程与外界换热的过程,不是单纯的绝热条件。
具体更可靠的计算,请读者参考GB/T 14513.3-2020中的方法。
4、结束语
假如你能阅读到这里,说明你对该问题有着同样的困惑和思考,希望这篇文章对你有所帮助。当然,这也仅仅是我个人对书本和网上所能搜到资料进行整理、推导,并加上自己的理解,难免会有错漏之处,如果你认为该文章有错误的地方,欢迎各位大佬后台私信交流。
互学互鉴,知识共享。