KMP算法的理解
KMP算法的理解
- 什么是KMP?
-
- 哪里提高了效率?
- KMP与一般算法的比较
-
- 一、一般算法(BF)
- 二、KMP算法匹配
- 重点:KMP算法中P串下一次定位到哪里呢?
- Final:next数组的缺陷与改进
什么是KMP?
KMP 是字符串模式匹配算法,在主串T中找到第一次出现完整子串P时的起始位置。是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的,称之为 Knuth-Morria-Pratt 算法。该算法相对于 Brute-Force(暴力)算法有比较大的改进,主要是消除了主串指针的回溯,从而使算法效率有了某种程度的提高。
哪里提高了效率?
上面说道 KMP 算法主要是通过消除主串指针的回溯来提高匹配的效率的,那么,它是则呢样来消除回溯的呢?就是因为它提取并运用了加速匹配的信息!
这种信息就是对于每模式串 P的每个元素 P j,都存在一个实数 k ,使得模式串 P开头的 k 个字符(P0,P1…Pk-1)依次与Pj前面的 k个字符(Pj-k,Pj-k+1…Pj-1相同,这里第一个字符Pj-k最少从P1开始,即 k < j,因为如果k=j,前k个和后k个都是从P0开始,包含了整个P j前的所有字符,无法起到筛选作用。如果这样的 k 有多个,则取最大的一个。模式串P中每个位置 j 的字符都有这种信息,采用 next 数组表示,即 next[ j ]=MAX{ k }。
提高效率的数组 next 的提取是整个 KMP 算法中最核心的部分,弄懂了 next 的求解方法,也就弄懂了 KMP 算法的十之七八了,但是不巧的是这部分代码恰恰是最不容易弄懂的……
KMP与一般算法的比较
一、一般算法(BF)
KMP算法要解决的问题就是在字符串(也叫主串)中的模式(pattern)定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字(接下来称它为P),如果它在一个主串(接下来称为T)中出现,就返回它的具体位置,否则未找到返回-1(常用手段)。
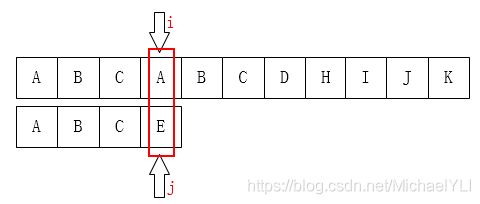
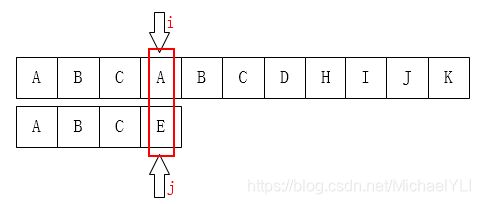
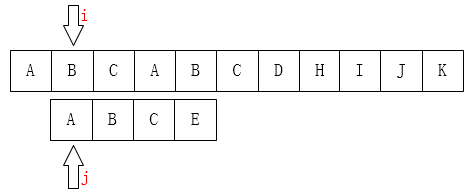
首先,对于这个问题有一个很直接的想法:从左到右一个个匹配,如果这个过程中有某个字符不匹配,就跳回去,将模式串向右移动一位。这有什么难的?之后我们只需要比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动,如果不一致:
A和E不相等,那就把i指针移回第1位(假设下标从0开始),j移动到模式串的第0位,然后又重新开始这个步骤
def match(T,P):
n,m=len(T),len(P)
i,j=0,0
while i<n and j<m:
if T[i]==p[j]:#相同,考虑下一对字符
i,j=i+1,j+1#递增i,j
else:
j=0#模式字符串重头开始匹配
i=i-j+1
if j==m:
return j-i
return -1
二、KMP算法匹配
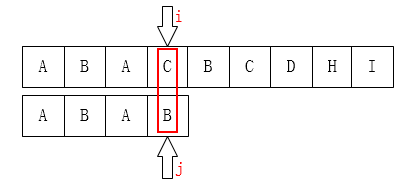
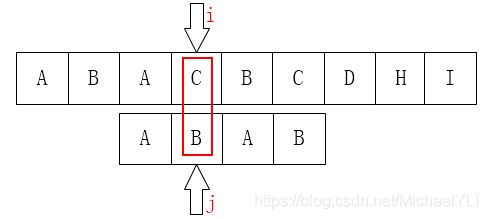
高效的寻找,肯定不会再把i移动回第1位,因为主串匹配失败的位置(i=3)前面除了第一个A之外再也没有A了,而且我们已经知道前面三个字符都是匹配的!(这很重要)那么移动过去肯定也是不匹配的!有一个想法,i可以不动,我们只需要移动j即可,如下图:直接i不动,j移动到0位
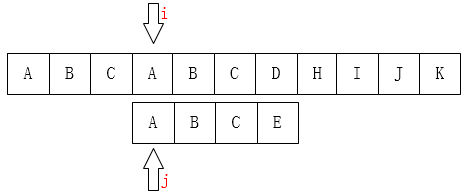
前一轮的比较中,我们已经知道了P的前(j-1)位与T中间对应的某(j-1)个元素已经匹配成功了。这就意味着,在一轮的尝试匹配中,我们get到了T主串的部分内容,我们能否利用这些内容,让P多移几位(我认为这就是KMP算法最根本的东西),减少遍历的趟数呢?答案是肯定的。再看下面改进后的动图:
这个模拟过程即KMP算法,若没有看明白,继续往下看相应的解释,理解需要把P多移几位,然后回头再看一遍这个图就很明了了。
相比朴素算法:
朴素算法: 每次失配,T串的索引i定位的本次尝试匹配的第一个字符的后一个。P串的索引j定位到0;T(n)=O(n*m)
KMP算法: 每次失配,T串的索引 i 不动,P串的索引 j 定位到某个数。T(n)=O(n+m),时间效率明显提高
重点:KMP算法中P串下一次定位到哪里呢?
假设模式串中前k个字符和Pj前的后k个字符相同,即
P [ 0 ∼ k − 1 ] = P [ j − k ∼ j − 1 ] P[0 \sim k-1]=P[j-k \sim j-1] P[0∼k−1]=P[j−k∼j−1]
当T[i] != p[j]时
必有 T [ i − j ∼ i − 1 ] = P [ 0 ∼ j − 1 ] T[i-j \sim i-1]=P[0 \sim j-1] T[i−j∼i−1]=P[0∼j−1]
由 P [ 0 ∼ k − 1 ] = P [ j − k ∼ j − 1 ] P[0 \sim k-1]=P[j-k \sim j-1] P[0∼k−1]=P[j−k∼j−1]得 T [ i − k ∼ i − 1 ] = T [ i − j ∼ i − j + k − 1 ] T[i-k \sim i-1]=T[i-j \sim i-j+k-1] T[i−k∼i−1]=T[i−j∼i−j+k−1]
所以 P [ 0 ∼ k − 1 ] = T [ i − k ∼ i − 1 ] P[0 \sim k-1]=T[i-k \sim i-1] P[0∼k−1]=T[i−k∼i−1]
这一段公式证明了我们为什么可以直接将j移动到k而无须再比较前面的k个字符。
定义:next[j]是接一个位置j所对应得k值。当子串 j位与主串 i位不匹配时,下一次和主串 i位比较的子串j位得值。
1、 j = 0 j=0 j=0时, P [ 0 ] ≠ T [ 0 ] P[0] \ne T[0] P[0]=T[0], j j j已经是最左边的位置了,无法前移,则后移 i i i,为计算方便令 n e x t [ 0 ] = − 1 next[0]=-1 next[0]=−1。
2、 j = 1 j=1 j=1时, P [ 1 ] ≠ T [ 1 ] P[1] \ne T[1] P[1]=T[1], j j j的前面只有0位,所以 n e x t [ 1 ] = 0 next[1]=0 next[1]=0.
求 n e x t [ j + 1 ] next[j+1] next[j+1],根据之前的分析, n e x t [ j + 1 ] next[j+1] next[j+1]的值为pj+1的前 j j j个元素的收尾重合的最大个数。即需要满足两个条件,把它的值一步步“检验”出来。一是“个数最多”的,因此要从可能的最大值开始验;二是“首尾重合”,因此要一一对应验是否相等。
规律:3、假设此时 n e x t [ j ] = k next[j]=k next[j]=k, P [ k ] = P [ j ] P[k] = P[j] P[k]=P[j], n e x t [ j + 1 ] next[j+1] next[j+1]的最大值 为 n e x t [ j ] + 1 next[j]+1 next[j]+1 ,因为 P [ 0 ∼ k − 1 ] = P [ j − k ∼ j − 1 ] P[0 \sim k-1]=P[j-k \sim j-1] P[0∼k−1]=P[j−k∼j−1],此时若 P [ k ] = P [ j ] P[k] = P[j] P[k]=P[j],则可以得到 P [ 0 ∼ k ] = P [ j − k ∼ j ] P[0 \sim k]=P[j-k \sim j] P[0∼k]=P[j−k∼j],所以 n e x t [ j + 1 ] = n e x t [ j ] + 1 next[j+1]=next[j]+1 next[j+1]=next[j]+1。
4、若 P [ k ] ≠ P [ j ] P[k] \ne P[j] P[k]=P[j],
①求 n e x t [ j + 1 ] next[j+1] next[j+1],设值为 m m m
②已知 n e x t [ j ] = k 1 next[j]=k1 next[j]=k1, k 1 ≤ m k1 \le m k1≤m ,则有 P [ 0 ∼ k 1 − 1 ] = P [ j − k 1 ∼ j − 1 ] P[0 \sim k1-1]=P[j-k1 \sim j-1] P[0∼k1−1]=P[j−k1∼j−1]
③已知 n e x t [ k 1 ] = k 2 next[k1]=k2 next[k1]=k2,则有 P [ 0 ∼ k 2 − 1 ] = P [ k 1 − k 2 ∼ k 1 − 1 ] P[0 \sim k2-1]=P[k1-k2 \sim k1-1] P[0∼k2−1]=P[k1−k2∼k1−1]
④此时 P [ 0 ∼ k 2 − 1 ] = P [ k 1 − k 2 ∼ k 1 − 1 ] = P [ j − k 1 ∼ j − k 1 + k 2 − 1 ] = P [ j − k 2 ∼ j − 1 ] P[0 \sim k2-1]=P[k1-k2 \sim k1-1]=P[j-k1\sim j-k1+k2-1]=P[j-k2 \sim j-1] P[0∼k2−1]=P[k1−k2∼k1−1]=P[j−k1∼j−k1+k2−1]=P[j−k2∼j−1],这四段一样。
⑤这时候,再判断如果 P [ k 2 ] = P [ j ] P[k2]=P[j] P[k2]=P[j],则 P [ 1 ∼ k 2 ] = P [ j − k 2 ∼ j ] P[1 \sim k2] = P[j-k2 \sim j] P[1∼k2]=P[j−k2∼j],则 n e x t [ j + 1 ] = k 2 + 1 next[j+1]=k2+1 next[j+1]=k2+1;否则再取 n e x t [ k 2 ] = k 3 next[k2]=k3 next[k2]=k3…以此类推
⑥一直未找到则 n e x t [ j + 1 ] = − 1 next[j+1]=-1 next[j+1]=−1

Final:next数组的缺陷与改进
显然,当我们上边的算法得到的next数组应该是[ -1,0,0,1 ]
不难发现,这一步是完全没有意义的。因为后面的B已经不匹配了,那前面的B也一定是不匹配的,同样的情况其实还发生在第2个元素A上。
显然,发生问题的原因在于 P [ j ] = = P [ n e x t [ j ] ] P[j] == P[next[j]] P[j]==P[next[j]]。
所以增加该情况的判断条件,令此时 n e x t [ j ] = n e x t [ n e x t [ j ] ] next[j]=next[next[j]] next[j]=next[next[j]]

def get_next(p):
'''
生成模式字符串的next数组
'''
j,k,m=0,-1,len(p)
nextlist=[-1]*m
while j<m-1:
if k==-1 or p[j]==p[k]:
j,k=j+1,k+1
nextlist[j]=k
if p[j]==p[k]:#已经改进
nextlist[j]=nextlist[k]
else:
k=nextlist[k]
return nextlist
def KMP(t,p):
j,i=0,0
n,m=len(t),len(p)
nextlist=get_next(p)
while i<n and j<m:
if j==-1 or t[i]==p[j]:
i,j=i+1,j+1
else:
j=nextlist[j]
if j==m:
return i-j
return -1