【Java】冒泡排序

一、什么是冒泡排序

定义

冒泡排序(bubble sort)是最基础的排序算法，它是一种基础的交换排序。它的原理就像汽水一样，汽水中常常有许多小气泡飘到上面。而冒泡排序这种排序算法的每一个元素也可以像小气泡一样根据自身大小一点点地向着数组一端移动。

那冒泡排序具体是如何移动的呢？

冒泡思想

对于以下这个无序的数列，用冒泡排序的思想进行排序：

冒泡排序的思想：相邻元素两两比较，当一个元素大于右侧相邻元素时，交换他们的位置；当一个元素小于或等于右侧元素时，位置不变。

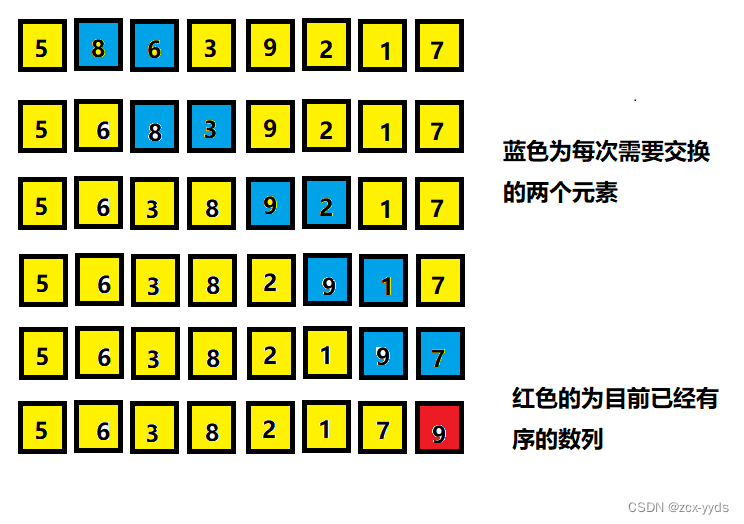
当通过一轮排序之后，元素9作为最大的元素，移动到了数列的最右端。9是目前有序数列的唯一元素。

总体的排序流程如下：

该算法每一轮排序都需要遍历一遍所有的元素，对于8个元素的排序总共遍历了7轮，所以该算法总共需要遍历(元素数量-1)轮，平均时间复杂度为O(n²);

代码实现

import java.util.Arrays;

public class bubbleSort {
    public static void sort(int arr[]) {
        //一共进行元素个数减一轮排序
        for (int i = 0; i < arr.length - 1; i++) {
            //只需要对没有排序的进行排序
            for (int j = 0; j < arr.length - 1 - i; j++) {
                //将前一个比后一个大的两元素进行交换
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                }
            }
        }
    }

    public static void main(String[] args) {
        int arr[] = {5, 8, 6, 3, 9, 2, 1, 7};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

二、冒泡排序的优化

第一次优化

从刚才的排序过程中我们可以发现到第六轮排序结束的时候数列已经是有序的了，但还要进行第七轮排序。对于这种情况，我们可以在数列有序时做出一个标志，那么就不用进行多余的排序了。

public static void sort(int arr[]) {
        //一共进行元素个数减一轮排序
        for (int i = 0; i < arr.length - 1; i++) {
            //有序的标志，每轮的初始值都为true
            boolean isSorted=true;
            //只需要对没有排序的进行排序
            for (int j = 0; j < arr.length - 1 - i; j++) {
                //将前一个比后一个大的两元素进行交换
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                    //如果有元素交换，说明数列还未有序
                    isSorted=false;
                }
            }
            //如果已经有序，则结束排序
            if(isSorted){
                break;
            }
        }
    }

第二次优化

我们还可以进一步对它进行优化，对于如下这个数列：

第一轮排序经过两次交换后变为：

然后接下来元素4和5进行比较，4小于5，位置不变。
元素5和6进行比较，5小于6，位置不变。
元素6和7进行比较，6小于7，位置不变。
元素7和8进行比较，7小于8，位置不变。

第一轮排序后我们可以发现，数列后面的几个数已经是有序的了，但还要进行几次比较，白白比较了很多次，这正是可以优化的地方。

为了避免这种情况的发生，我们可以在每轮排序后记录下最后一次元素交换的位置，该位置为无序数列的边界，该位置以后为有序区。

public static void sort(int arr[]) {
        //最后一次进行元素交换的位置
        int lastExchangeIndex=0;
        //无序数列的边界，每次排序只需要到这个元素
        int sortBorder=arr.length-1;
        //一共进行元素个数减一轮排序
        for (int i = 0; i < arr.length - 1; i++) {
            //有序的标志，每轮的初始值都为true
            boolean isSorted=true;
            //只需要对没有排序的进行排序
            for (int j = 0; j < sortBorder; j++) {
                //将前一个比后一个大的两元素进行交换
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                    //如果有元素交换，说明数列还未有序
                    isSorted=false;
                    //更新最后一次交换的位置
                    lastExchangeIndex=j;
                }
            }
            sortBorder=lastExchangeIndex;
            //如果已经有序，则结束排序
            if(isSorted){
                break;
            }
        }
    }

三、鸡尾酒排序

冒泡排序都是每一轮从左到右来比较元素，进行单向的位置交换。

而鸡尾酒排序每次元素的比较与交换过程是双向的。

对于以上数列，只有元素1的位置不对，但使用冒泡排序却需要进行7轮排序，鸡尾酒排序刚好可以解决这个问题。

第一轮：

第一轮与冒泡排序一样，8和1进行交换

第二轮：

第二轮换为从右往左进行比较交换

第三轮：

虽然此时已经有序，但流程还未结束，第三轮重新开始从左到右进行比较交换。
几次比较之后没有位置进行交换，排序结束。三轮就已经有序。

鸡尾酒排序第一轮从左到右，第二轮从右到左，第三轮再从左到右…直至数列有序。

public static void sort(int arr[]){
        //鸡尾酒排序每两轮会在数列两端各增加一个有序的的元素，下一轮不用再进行比较
        for (int i = 0; i < arr.length/2; i++) {
            //有序标记，初始值为true
            boolean isSorted=true;
            //奇数轮，从左向右比较交换
            for (int j = i; j < arr.length-i-1; j++) {
                if(arr[j]>arr[j+1]){
                    int tmp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=tmp;
                    //有元素交换，所以不是有序的
                    isSorted=false;
                }
            }
            //如果已经有序，则结束排序
            if(isSorted){
                break;
            }
            //偶数轮前，isSorted重新置为true
            isSorted=true;
            //偶数轮，从右向左进行比较交换
            for (int j = arr.length-i-1; j > i; j--) {
                if(arr[j]<arr[j-1]){
                    int tmp=arr[j];
                    arr[j]=arr[j-1];
                    arr[j-1]=tmp;
                    //有元素交换，所以不是有序的
                    isSorted=false;
                }
            }
            if(isSorted){
                break;
            }
        }
    }

鸡尾酒排序的优势是在大多数元素已经有序的情况下减少了排序的回合数，但缺点是代码量增加了近一倍。