第三章 灰度变换与空间滤波

3灰度变换与空间滤波

3.1背景知识

3.1.1灰度变换和空间滤波基础

本章讨论的空间域处理可有下式表示$$g(x,y)=T[f(x,y)]$$其中，$f(x,y)$是输入图像，$g(x,y)$是处理后的图像，$T$是在点$(x,y)$的领域上定义的关于的一种算子。
最小邻域为1x1。此时$g$仅取决于点$(x,y)$的$f$值，T成为灰度函数：$$s=T(r)$$

3.2一些基本的灰度变换函数

3.2.1图像反转

原灰度图像的灰度范围[0,L-1],反转：$$s=L-1-r$$

def img_reverse(img):
    img2 = np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img2[x][y] = 255-img[x][y]
    return img2.astype(np.uint8)


img = cv2.imread('AM.png', 0)
img2 = img_reverse(img)
plt_show(img, img2)

即黑变白，白变黑

3.2.2对数变换

对数变换的通用形式$$s=c\log (1+r)$$

假设公式为$s=c{\log }_k(1+r)$，（L-1,L-1）符合映射，应有$L-1=c{\log }_k(1+L-1)$，可得$$c=\frac{L-1}{{\log }_{k}L}$$当L=256时，可得$$c=\frac{255}{{\log }_{k}256}$$

# 对数变换的灰度示意图
def get_c(k):
    return 255*math.log(k)/math.log(256)


c = get_c(math.e)
x = np.arange(0, 255, 0.01)
plt.plot(x, x)
plt.plot(x, c*np.log(x+1))

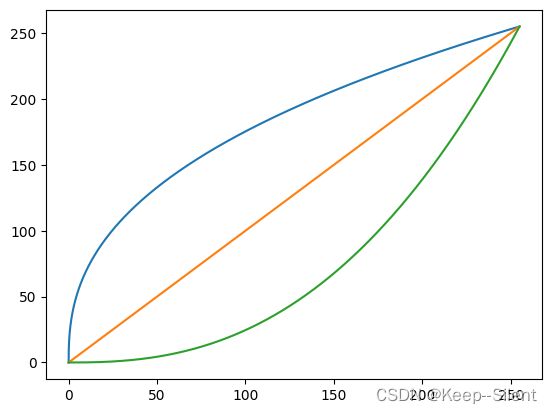
该图中对数曲线的形状表明，该变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值

# 对数变换的例子
def funT(c, r, k):
    return c*math.log(1+r, k)


def get_log_img(img, k):
    c = get_c(k)
    img2 = np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img2[x][y] = funT(c, img[x][y], k)
    return img2.astype(np.uint8)


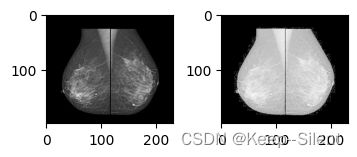
img = cv2.imread('X.png', 0)
img2 = get_log_img(img, k=math.e)
plt_show(img, img2)

实验表明，我们可以使用这种类型的变换来扩展图像中的暗像素的值，同时压缩更高灰度级的值。

3.2.3幂律（伽马）变换

幂律变换的基本形式为：$$s=c{r}^{\gamma }$$（L-1,L-1）符合映射，应有$L-1=c(L-1{)}^{\gamma }$，可得$$c=\frac{L-1}{(L-1{)}^{\gamma }}$$当L=256时，可得$$c=\frac{255}{255^{\gamma }}$$

# 幂律变换的灰度示意图
def get_c(gamma):
    return 255/255**gamma


gammas = [0.4, 1, 2.5]
x = np.arange(0, 255, 0.01)
for gamma in gammas:
    c = get_c(gamma)
    plt.plot(x, c*np.power(x,gamma))

如图所示，与对数变换的情况类似，部分$\gamma$值的幂律曲线将较窄范围的暗色输入值映射为较宽范围的输出值,相反地，对于输入高灰度级值时也成立。然而,与对数函数不同的是，随着$\gamma$值的变化,将简单地得到一族可能的变换曲线。示意图表明，$\gamma$>1的值所生成的曲线和$\gamma$<1的值所生成的曲线的效果完全相反，在$c=\gamma =1$时简化成了恒等变换。

# 幂律变换的例子
def funT(r):
    return c*r**gamma


img = cv2.imread('lena.jpg', 0)
imgs = []
gammas = [0.4, 1, 2.5]
for gamma in gammas:
    img_t = np.zeros(img.shape)
    c = get_c(gamma)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y] = funT(img[x][y])
    imgs.append(img_t.astype(np.uint8))
plt_show(imgs[0], imgs[1], imgs[2])

不恰当校正的图片看起来不是太亮就是太暗，可以通过此方法进行校正。

3.2.4分段线性变换函数

对比度拉伸

# 对比度拉伸示意图
def getLine(x1, y1, x2, y2):
    k = (y1-y2)/(x1-x2)
    b = y1-k*x1
    return k, b


def funT(r):
    lines = [getLine(0, 0, rs1[0], rs1[1]),
             getLine(rs2[0], rs2[1], rs1[0], rs1[1]),
             getLine(255, 255, rs2[0], rs2[1]),]
    if r <= rs1[0]:
        index = 0
    elif r <= rs2[0]:
        index = 1
    else:
        index = 2
    return int(lines[index][0]*r+lines[index][1])


x = np.arange(0, 256, 1)
point1 = [[100, 50], [156, 206]]
point2 = [[127, 0], [128, 255]]
point3 = [[1, 1], [3, 3]]
for rs1, rs2 in point3, point1, point2:
    y = np.array([funT(r) for r in x])
    plt.plot(x, y)
# plt.plot(x, funT(x))

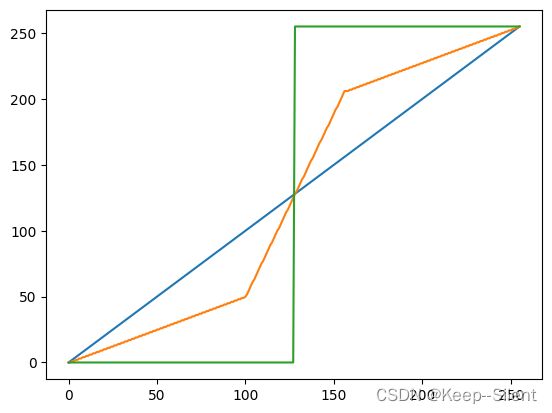
上图显示了一个用于对比度拉伸的典型变换。点$(r_1,s_1)$和点$(r_2,s_2)$的位置控制变换函数的形状。如果$r_1=s_1$且$r_2=s_2$，则变换为线性函数，将产生一个没有变化的灰度级。若$r_1=r_2$,$s_1=0$且$s_2=L-1$，则变换变为阈值处理函数，并产生一幅二值图像，如下所示。

img0 = cv2.imread('jmu.jpg')
img0 = img0[200:700, 450:800]
img1 = cv2.cvtColor(img0, cv2.COLOR_RGB2GRAY)
imgs = []
for rs1, rs2 in point3, point1, point2:
    img_t = np.zeros(img1.shape)
    for x in range(len(img1)):
        for y in range(len(img1[x])):
            img_t[x][y] = funT(img1[x][y])
    imgs.append(img_t.astype(np.uint8))

plt_show(img1,imgs[0],imgs[1],imgs[2])

从上到下、从左到右依次是img0：imgs[0]、imgs[1]、imgs[2]
img0：原图
imgs[0]：没有变化
imgs[1]：影响对比度
imgs[2]：二值图像

灰度级分层

# 灰度级分层示意图
def funT1(r):
    a, b = 70, 150
    return 200 if a <= r <= b else 0


def funT2(r):
    a, b = 200, 270
    return 255 if a <= r <= b else r


x = np.arange(0, 256, 1)
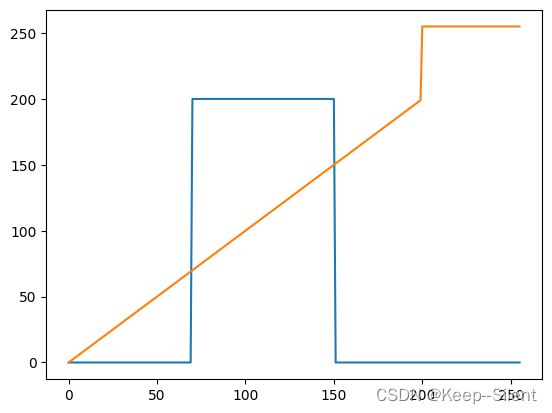
plt.plot(x, np.array([funT1(r) for r in x]))
plt.plot(x, np.array([funT2(r) for r in x]))

# 灰度级分层例子
img = cv2.imread('jmu.jpg', 0)[150:800, 450:800]
img2, img3 = np.zeros(img.shape),np.zeros(img.shape)
for x in range(len(img)):
    for y in range(len(img[x])):
        img2[x][y] = funT1(img[x][y])
        img3[x][y] = funT2(img[x][y])
img2=img2.astype(np.uint8)
img3=img3.astype(np.uint8)
plt_show(img,img2,img3)

img：原图的灰度图
img2：感兴趣区域设为200，其余黑色
img3：感兴趣区域设为白色，其余不变

比特平面分层
灰度图中，每个像素是由1个8比特组成，现看做8个1比特进行分层

img=cv2.imread('me.jpg',0)
imgs=[img]
for i in range(8):
    img_t = np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y] = (img[x][y]>>i)<<7
    imgs.append(img_t.astype(np.uint8))
plt_show(imgs[0],imgs[1],imgs[2],
        imgs[3],imgs[4],imgs[5],
         imgs[6],imgs[7],imgs[8],)

上图是原图和8个比特分层图。
上图表明：高比特包含了视觉上很重要的大多数数据，而低比特在图像中贡献了更多精细的灰度细节。

img=cv2.imread('me.jpg',0)
imgs=[]
for i in range(3):
    img_t = np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y] = (img[x][y]>>(6-i))<<(6-i)
    imgs.append(img_t.astype(np.uint8))
imgs.append(img)
img_t = np.zeros(img.shape)
for x in range(len(img)):
    for y in range(len(img[x])):
        img_t[x][y] = img[x][y]-imgs[2][x][y]
imgs.append(img_t.astype(np.uint8))
plt_show(imgs[0],imgs[1],imgs[2],
         imgs[3],imgs[4],
        )

上图分别是：

1. 使用比特面8、7重建的图像
2. 使用比特面8、7、6重建的图像
3. 使用比特面8、7、6、5重建的图像
4. 原图的灰度图
5. 4和3相减

可以看出，高四个比特占主要效果，低四个比特几乎不影响效果。由此可知，仅存储高四个比特，可以减少一半的储存量。

3.3直方图处理

直方图由$p(r_k)=\frac{n_k}{MN}$产生，其$k=0,1,\dots ,L-1$、$r_k$表示灰度值，$n_k$表示该灰度值的数量

3.3.1直方图均衡

def get_c(gamma):
    return 255/255**gamma


def funT(r):
    return c*r**gamma


img = cv2.imread('castle.png', 0)
imgs = []
gammas = [0.3, 1, 4]
for gamma in gammas:
    img_t = np.zeros(img.shape)
    c = get_c(gamma)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y] = funT(img[x][y])
    imgs.append(img_t.astype(np.uint8))
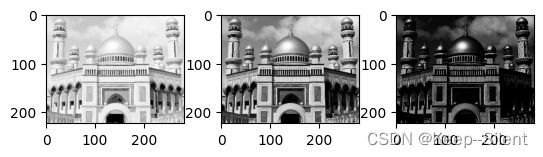
plt_show(imgs[0], imgs[1], imgs[2])

上图分别是亮图、原图、暗图，后用以显示直方图

def hist_show(img,name):#展示图片的直方图
    v=img.reshape(-1)
    n=len(v)
    plt.hist(v,weights=[1/n]*n,bins=64, alpha=0.5,label=name)
    plt.legend()
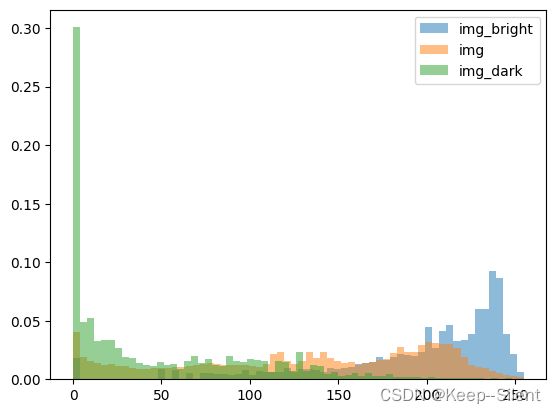
hist_show(imgs[0],'img_bright')
hist_show(imgs[1],'img')
hist_show(imgs[2],'img_dark')

可以看出亮图总体灰度较高，暗图灰度较低。
直方图均衡的核心公式：$$s=T(r)=(L-1){\int }_0^r{p}_r(w)\text{d}w$$ 即，$(L-1)$ * 概率前缀和。
接下来进行直方图效果展示。

可以看出经过处理，直方图很均衡。
现对“亮图、原图、暗图”进行直方图均衡处理。

def getImgProbability(img):#  得到概率
    v=img.reshape(-1)
    n=len(v)
    k=1/n
    dt={i:0 for i in range(256)}
    for t in v:
        dt[t]+=k
    return [dt[t] for t in dt]
def histogramEqualization(img): #得到T(r)
    weight2=getImgProbability(img)
    for t in range(1,256):
        weight2[t]+=weight2[t-1]
    return [x*255 for x in weight2]

imgEqualizations=[]
for img in imgs:
    Tr=histogramEqualization(img)
    img_t=np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y]=int(Tr[img[x][y]])
    imgEqualizations.append(img_t.astype(np.uint8))
plt_show(imgs[0],imgs[1],imgs[2],
    imgEqualizations[0],imgEqualizations[1],imgEqualizations[2])

上诉图片的依次是：
亮图，原图，暗图
亮图均衡后，原图均衡后，暗图均衡后。
实验表明，因为图像有相同的内容，直方图均衡导致的对比度增强足以补偿图像在视觉上难以区分灰度级的差别。在给出原始图像间的重要对比度差别后，该例说明了直方图均衡作为自适应对比度增强工具的强大作用。

Tr=histogramEqualization(imgs[0])
plt.hist(range(256),weights=Tr,bins=256, alpha=0.5,label='T(r)')
plt.legend()

上图为Tr效果图

img_bright=imgs[0]
img_bright_equalization=imgEqualizations[0]

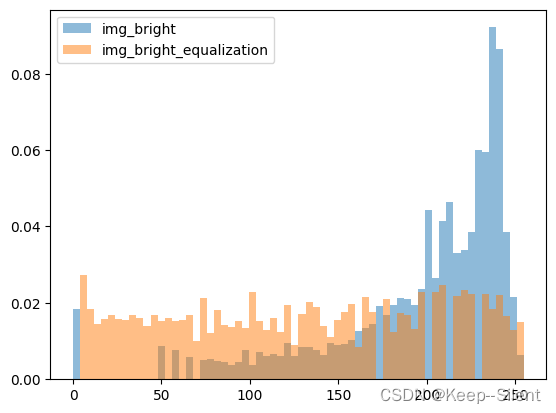
plt.hist(range(256),weights=getImgProbability(img_bright),bins=64, alpha=0.5,label='img_bright')
plt.hist(range(256),weights=getImgProbability(img_bright_equalization),bins=64, alpha=0.5,label='img_bright_equalization')
plt.legend()

上图为亮图、亮图概率均衡后的直方图。可以看出经过均衡操作，概率比原来均衡多了

3.3.2直方图匹配（规定化）

对于某些应用，采用均匀直方图的基本增强不是最好的方法。有时，处理后的图像具有规定的直方图形状可能更有用，此为直方图匹配（或直方图规定化）。

直方图均衡的核心公式为$$s=T(r)=(L-1){\int }_0^r{p}_r(w)\text{d}w$$而直方图匹配的公式为$$G(z)=(L-1){\int }_0^r{p}_z(w)\text{d}w$$其中$p_z(w)$为自定义的函数，其可以根据需求产生需要的直方图。

def histogramStandardization(pw):
    for t in range(1,256):
        pw[t]+=pw[t-1]
    return [x*255 for x in pw]
pw1=[0]*156+[0.01]*100
pw2=[0]*30+[0.01]*100+[0]*126
img=cv2.imread('yby.jpg',0)
imgStandardizations=[img]
for pw in pw1,pw2:
    Tr=histogramStandardization(pw)
    img_t=np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y]=int(Tr[img[x][y]])
    imgStandardizations.append(img_t.astype(np.uint8))
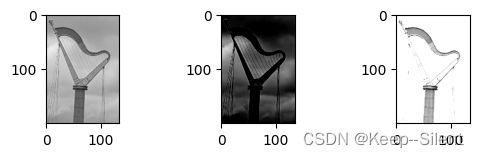
plt_show(imgStandardizations[0],imgStandardizations[1],imgStandardizations[2])

上图为：原图，规定的暗图，规定的亮图。
暗图中，可以看到云彩更多的细节。

3.3.3局部直方图处理

img=cv2.imread('caigou.jpg',0)
x_zhou = np.arange(0, 256, 1)
y_zhou=np.array([0,0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 12, 12, 13, 13, 14, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 21, 22, 23, 24, 25, 26, 27, 29, 30, 31, 32, 34, 35, 36, 38, 39, 40, 42, 43, 45, 46, 48, 50, 51, 53, 56, 59, 61, 64, 66, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 90, 92, 95, 97, 100, 102, 105, 108, 111, 114, 116, 119, 122, 125, 128, 130, 133, 136, 139, 141, 144, 147, 150, 153, 157, 160, 162, 165, 168, 171, 174, 177, 179, 183, 186, 189, 192, 194, 197, 200, 202, 205, 207, 210, 221, 227, 232, 234, 236, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 250, 251, 252, 252, 253, 253, 253, 254, 254, 254, 254, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255, 255])
print([type(x_zhou),type(y_zhou)])
print([len(x_zhou),len(y_zhou)])
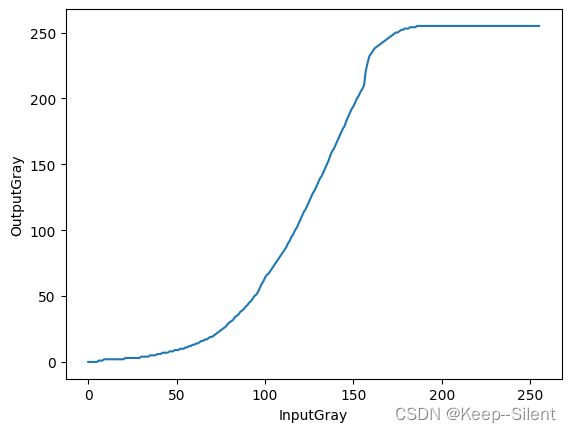
plt.xlabel ("InputGray")
plt.ylabel ("OutputGray")
plt.plot(x_zhou, y_zhou)
plt.show()


img2=np.zeros(img.shape)
for x in range(len(img)):
    for y in range(len(img[x])):
        img2[x][y]=int(y_zhou[img[x][y]])
img2=img2.astype(np.uint8)
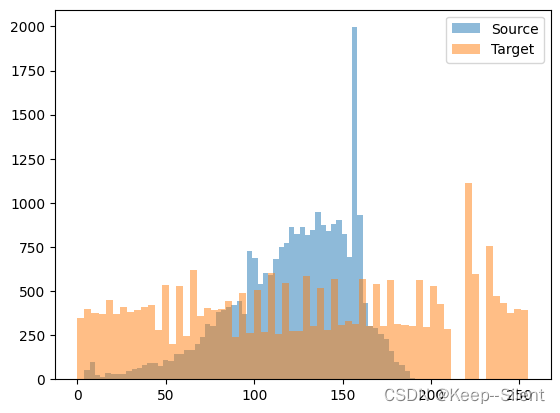
plt.hist(img.reshape(-1),bins=64, alpha=0.5,label='Source')
plt.hist(img2.reshape(-1),bins=64, alpha=0.5,label='Target')
plt.legend()

以图像中每个像素的邻域的灰度分布为基础，设计变换函数y_zhou
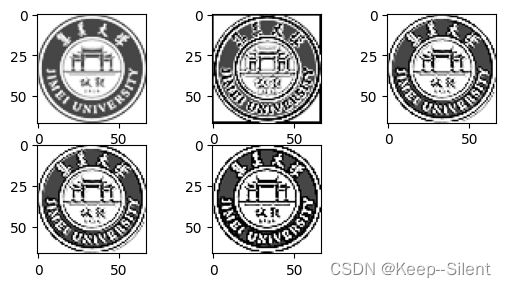
灰度变换函数如上图1所示，灰度像素级如图2所示。

效果如下图“菜狗”所示，图像得到增强

3.3.4在图像增强中使用直方图统计

$r$ 为区间$[0,L-1]$上的灰度的离散随机变量，$p(r_i)$表示$r_i$上对应$r$值的归一化直方图分量，$r$关于其均值的n阶矩定义为$${\mu }_n(r)=\sum _{i=0}^{L-1}(r_i-m{)}^{n}p(r_i)$$ $m$ 为 $r$ 的均值（平均灰度）：$$m=\sum _{i=0}^{L-1}{r}_{i}p(r_i)$$ 其中二阶矩特别重要：$${\mu }_2(r)=\sum _{i=0}^{L-1}(r_i-m{)}^{2}p(r_i)$$

3.4空间滤波基础

“滤波”是指接受(通过)或拒绝一定的频率分量。例如，通过低频的滤波器称为低通滤波器。低通滤波器的最终效果是模糊(平滑)一幅图像。我们可以用空间滤波器(也称为空间掩模、核、模板和窗口)直接作用于图像本身而完成类似的平滑。

3.4.1空间滤波机理

使用$m\ast n$的滤波器对图像进行线性空间处理（$m=2a+1,n=2b+1$）：$$g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)$$ 如3x3：$$g(x,y)=w(-1,-1)f(x-1,y-1)+w(-1,0)f(x-1,y)+\cdots +w(0,0)f(x,y)+\cdots +w(1,1)f(x+1,y+1)$$

3.4.2空间相关与卷积

$$w(x,y)★f(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x-s,y-t)$$

3.4.3线性滤波的向量表示

采用向量形式，方便计算：$$R=w_1{z}_1+w_2{z}_2+\cdots +w_{mn}{z}_{mn}=\sum _{k=1}^{mn}{w}_k{z}_k=w^{T}z$$

3.4.4空间滤波模板的产生

3x3的邻域，平均灰度为$$R=\frac{1}{9}\sum _{i=1}^9{z}_i$$一个具有两个变量的高斯函数有如下的基本形式：$$h(x,y)={\mathrm{e}}^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

3.5平滑空间滤波器

3.5.1平滑线性滤波器

一幅M×N的图像经过一个大小为mxn (m和n是奇数)的加权均值滤波器滤波的过程可由下式给出:$$g(x,y)=\frac{\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)}{\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)}$$

假设滑动窗口步长$S$，滤波器尺寸$F_W\ast F_H$，边缘填充$P$，原宽度和新宽度的关系：$$W_2=\frac{W_1-F_W+2P}{S}+1$$令$W_1=W_2=m,F_W=size$ ，则有$$P=\frac{(m-1)S-m+size}{2}$$令$S=size=1$ 则有
即$$P=\frac{size-1}{2}$$

def WaveFilter(img,w):
    size=len(w)
    n,m=len(img),len(img[0])
    img2=np.zeros([n,m])
    img=np.pad(img,(size-1)//2)
    for x in range(n):
        for y in range(m):
            f=img[x:x+size,y:y+size]
            img2[x][y]=np.vdot(f,w)  
    img2=img2.astype(np.uint8)
    return img2   
sizes=[1,3,5,9,15,35]
img=cv2.imread('a.png',0)
imgs=[]
for size in sizes:
    w=np.array([1/size/size]*(size*size)).reshape(size,-1)
    img2=WaveFilter(img,w)
    imgs.append(img2)
    print(w.size)
plt_show(imgs[0],imgs[1],imgs[2],
        imgs[3],imgs[4],imgs[5],)

上图分别采用[1,3,5,9,15,35]的尺寸进行图像平滑。可以看出，随着滤波器尺寸的增大，一些小点逐渐消失不见，但是图片也逐渐变得模糊。

3.5.2统计排序滤波器

如中值滤波器

import random
def ZhongzhiFilte(img,size):
    n,m=len(img),len(img[0])
    img2=np.zeros([n,m])
    img=np.pad(img,(size-1)//2)
    for x in range(n):
        for y in range(m):
            f=img[x:x+size,y:y+size].reshape(-1)
            f.sort()
            img2[x][y]=f[size*size//2] 
    img2=img2.astype(np.uint8)
    return img2   
def wuran(img):
    img2=copy.deepcopy(img)
    n,m=len(img),len(img[0])  
    level=30
    for x in range(n):
        for y in range(m):
            k=random.randint(0,2*level)
            if k%level==0:
                k//=level
                if k%2:
                    img2[x][y]=0
                else:
                    img2[x][y]=255
    return img2
img=cv2.imread('flower.png',0)
img_wuran=wuran(img)
img_junzhi=WaveFilter(img_wuran,np.array([[1/9]*3]*3))
img_zhongzhi=ZhongzhiFilte(img_wuran,3)
plt_show(img,img_wuran,img_junzhi,img_zhongzhi)

四图分别是

1. 原图
2. 随机污染后的图
3. 均值滤波器操作后的图
4. 中止滤波器操作后的图

显然，中值滤波器效果比均值滤波器效果好

3.6锐化空间滤波器

锐化处理的主要目的是突出灰度过渡部分

3.6.1基础

一维函数$f(x)$的一阶微分为差值$$\frac{\partial f}{\partial x}=f(x+1)-f(x)$$由此，可推得二阶微分函数为$$\frac{{\partial }^{2}f}{\partial x^2}=f(x+1)+f(x-1)-2f(x)$$二阶微分在增强细节方面比一阶微分好得多，所以接下来主要注意二阶微分。

3.6.2使用二阶微分进行图像锐化——拉普拉斯算子

二维函数$f(x,y)$的拉普拉斯算子定义为$${\nabla }^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$在x和y的方向上分别有$$\{\begin{array}{l}\frac{{\partial }^{2}f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)\\ \\ \frac{{\partial }^{2}f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y)\end{array}$$联立可得$${\nabla }^{2}f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$$我们使用拉普拉斯对图像增强的基本方法可表示为：$$g(x,y)=f(x,y)+c[{\nabla }^{2}f(x,y)]$$

常见的算子有：$$\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}\begin{array}{ccc}0& -1& 0\\ -1& 4& -1\\ 0& -1& 0\end{array}\begin{array}{ccc}-1& -1& -1\\ -1& 8& -1\\ -1& -1& -1\end{array}$$现采用这四种算子进行图像增强

def WaveFilter(img,w):
    size=len(w)
    n,m=len(img),len(img[0])
    img2=np.zeros([n,m])
    img=np.pad(img,(size-1)//2)
    for x in range(n):
        for y in range(m):
            f=img[x:x+size,y:y+size]
            img2[x][y]=np.vdot(f,w) +img[x][y]         
            if img2[x][y]<0:
                img2[x][y]=0
            elif img2[x][y]>255:
                img2[x][y]=255
    img2=img2.astype(np.uint8)
    return img2 
  
img=cv2.imread('jimei.png',0)[:,:67]
print(img.shape)
ws=[    [[0,1,0],[ 1,-4,1],[ 0,1,0]],
        [[1,1,1],[ 1,-8,1],[ 1,1,1], ],
        [[0,-1,0],[ -1,4,-1],[ 0,-1,0]],
        [[-1,-1,-1],[ -1,8,-1],[ -1,-1,-1]],]
imgs=[img]
for w in ws:
    img2=WaveFilter(img,w)
    imgs.append(img2)
    print(w)
plt_show(imgs[0],imgs[1],imgs[2],
        imgs[3],imgs[4],)

可以看出，这些图像的细节比原图像更清晰。

3.6.3非锐化掩蔽和高提升滤波

非锐化掩蔽（原图像中减去一幅非锐化（平滑过的）版本）：

1. 模糊原图像
2. 从原图像中减去模糊图像（差值图像为模板图像）
3. 将模板加到原图像上

令$\overline{f}(x,y)$表示模糊图像，非锐化掩蔽以公式形式描述如下。首先，我们得到模板：$$g_{\text{mask}}(x,y)=f(x,y)-\overline{f}(x,y)$$然后，在原图像上加上该模板的一个权重部分：$$g(x,y)=f(x,y)+k\ast g_{\mathrm{mask}}(x,y)$$ $k=1$时，非锐化掩蔽；$k>1$时，高提升滤波

def WaveFilter(img,w):
    size=len(w)
    n,m=len(img),len(img[0])
    img2=np.zeros([n,m])
    img=np.pad(img,(size-1)//2)
    # print(img2.shape)
    for x in range(n):
        for y in range(m):
            f=img[x:x+size,y:y+size]
            img2[x][y]=np.vdot(f,w)  
    img2=img2.astype(np.uint8)
    return img2   

img=cv2.imread('point.png',0)
size=7
img_hu=WaveFilter(img,np.array([[1/size/size]*size]*size))
print(img.shape)
img_det=img-img_hu
img_feiruihuayanbi=img-img_det
img_gaotishenglvbo=img-img_det*4
plt_show(img,img_hu,img_det,
         img_feiruihuayanbi,img_gaotishenglvbo)

(200, 206)

上图分别为：

1. 原图
2. 模糊图
3. 差值图（即模板）
4. 非锐化掩蔽图（k=1）
5. 高提升滤波图（k=4）

该高提升滤波图和原图像相比有了较大改进

3.6.4使用一阶微分对(非线性)图像锐化——梯度

二维梯度定义 ∇ f ≡ gcd ⁡ ( f ) ≡ [ g x g y ] = [ ∂ f ∂ x ∂ f ∂ y ] \nabla f\equiv\gcd(f)\equiv\begin{bmatrix}g_x\\ g_y\end{bmatrix}=\begin{bmatrix}\cfrac{\partial f}{\partial x}\\ \\ \cfrac{\partial f}{\partial y}\end{bmatrix} ∇f≡gcd(f)≡[gx​gy​​]= ​∂x∂f​∂y∂f​​ ​ 算子$$\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}$$

def WaveFilter(img,w):
    size=len(w)
    n,m=len(img),len(img[0])
    img2=np.zeros([n,m])
    img=np.pad(img,(size-1)//2)
    for x in range(n):
        for y in range(m):
            f=img[x:x+size,y:y+size]
            img2[x][y]=np.vdot(f,w) +img[x][y]         
            if img2[x][y]<0:
                img2[x][y]=0
            elif img2[x][y]>255:
                img2[x][y]=255
    img2=img2.astype(np.uint8)
    return img2 
w=[ [-1,-2,-1],[0,0,0],[1,2,1], ]
img=cv2.imread('jmu_.jpg',0)
imgt=WaveFilter(img,w)
cv2.imwrite('jmu_gray.jpg',img)
cv2.imwrite('jmu_tidu.jpg',imgt)

上图为灰度图和其梯度效果