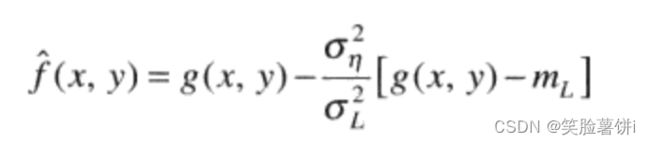【数字图像处理 第五章 图像复原与重建】
数字图像处理 第五章 图像复原与重建
- 引言
- 5.1 图像退化/复原过程的模型
- 5.2 噪声模型
-
- 5.2.1 噪声的空间和频率特性
- 5.2.2 重要的噪声概率密度函数(PDF)
- 高斯噪声
-
- 实验代码
- 实验结果
- 实验结果
- 椒盐噪声
-
- 实验代码
- 实验结果
- 实验结果
- 噪声图像及其直方图
- 周期噪声
- 噪声参数估计
- 5.3 只存在噪声的复原——空间滤波
-
- 5.3.1 均值滤波器
- 5.3.2 统计排序滤波器
- 5.3.3 自适应滤波器
-
- 自适应局部降低噪声滤波器
- 自适应中值滤波器
- 实验之Python实现自适应中值滤波法去除椒盐噪声
- 5.4 用频率波消除周期噪声
- 5.5 线性、位置不变的退化
- 5.6 估计退化函数
-
- 5.6.1 图像观察估计法
- 5.6.2 试验估计法
- 5.6.3 模型估计法
- 5.7 逆滤波
- 5.8 最小均方误差(维纳)滤波
-
- 实验之用维纳滤波去除运动引起的图像模糊
- 5.9 约束最小二乘方滤波
- 5.10 几何均值滤波
- 5.11 由投影重建图像
-
- 5.11.1 引言
-
- 反投影法
- 反投影复原出二维图像
- 5.11.2 计算机断层(CT)原理
- 5.11.3 投影和雷登变换
- 5.11.4 傅里叶切片定理
引言
图像复原技术的主要目的是以预先确定的目标来改善图像。
与图像增强相比,虽然两者有相覆盖的领域,但是图像增强主要是一个主观过程,其目的是改善图片的质量,对感兴趣的部分加以增强,对不感兴趣的部分予以抑制。
而图像复原大部分是一个客观过程,针对质量降低或失真的图像,试图恢复其原始的内容或质量。
图像复原试图利用退化现象的某种先验知识来复原被退化的图像。
因此,复原技术是面向退化模型的,并且采用相反的过程处理,以便恢复出原图像。在进行图像复原之前要先建立起其退化模型,根据该模型进行图像复原。
5.1 图像退化/复原过程的模型
如图5.1所示,在本章中,图像退化过程建模为一个退化函数和一个加性噪声项。
对一幅输入图像f(x,y)进行处理,产生一幅退化后的图像g(x,y)。
给定g(x,y)和关于退化函数H的一些知识以及关于退化函数H的一些知识以及关于加性噪声项η(x,y)的一些知识后,图像复原的目的就是获得原始图像的一个估计f*(x,y)。
本章节中使用的大部分复原方法都是以不同类型的图像复原滤波器为基础的。
若H是线性的,位置不变的过程,则空间域中的退化图像由下式给出:
g(x,y)=h(x,y)∗f(x,y)+δ(x,y)
其中,h(x, y)是退化函数的空间表示,符号∗表示卷积。
空间域的卷积和频域的乘法组成了一个傅里叶变换对,所以可以用等价的频域表示来写出前面的模型:
G(u,v)=H(u,v)F(u,v)+N(u,v)
5.2 噪声模型
数字图像处理的噪声主要来源于图像的获取(数字化过程)和传输过程。成像传感器的工作情况受各种因素的影响,如图像获取中的环境条件和传感元器件自身的质量。
模拟噪声特性和影响能力是图像复原的核心。
5.2.1 噪声的空间和频率特性
与我们讨论相关的是定义噪声空间特性的参数,以及噪声是否与图像相关。
频率特性是指傅里叶域中噪声的频率内容(即相对于电磁波谱的频率)。
除空间周期噪声之外,在本章中假设噪声独立于空间坐标,并且噪声与图像本身不相关(即像素值与噪声分量的值之间不相关)。
5.2.2 重要的噪声概率密度函数(PDF)
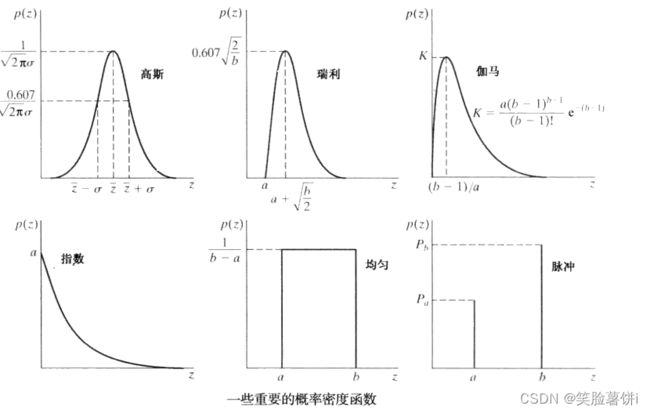
本章中举例的一些比较重要的噪声:高斯噪声,瑞利噪声,爱尔兰(伽马)噪声,指数噪声,均匀噪声,脉冲(椒盐)噪声。
高斯噪声
用python实现添加高斯噪声。
实验代码
import numpy as np
import cv2
def gasuss_noise(image, mu=0.0, sigma=0.1):
"""
添加高斯噪声
:param image: 输入的图像
:param mu: 均值
:param sigma: 标准差
:return: 含有高斯噪声的图像
"""
image = np.array(image / 255, dtype=float)
noise = np.random.normal(mu, sigma, image.shape)
gauss_noise = image + noise
if gauss_noise.min() < 0:
low_clip = -1.
else:
low_clip = 0.
gauss_noise = np.clip(gauss_noise, low_clip, 1.0)
gauss_noise = np.uint8(gauss_noise * 255)
return gauss_noise
if __name__ == '__main__':
# ----------------------读取图片-----------------------------
img = cv2.imread("D:\\study\\jimei.jpg")
# --------------------添加高斯噪声---------------------------
out2 = gasuss_noise(img, mu=0.0, sigma=0.1)
# ----------------------显示结果-----------------------------
cv2.imshow('origion_pic', img)
cv2.imshow('gauss_noise', out2)
cv2.waitKey(0)
实验结果
实验结果
高斯噪声就是给图片添加一个服从高斯分布的噪声,可以通过调节高斯分布标准差(sigma)的大小来控制添加噪声程度,sigma越大添加的噪声越多图片损坏的越厉害。
本实验将sigma设为0.1。高斯噪声出现在图像的所有位置。
椒盐噪声
用python实现添加椒盐噪声。
实验代码
import cv2
import numpy as np
#读取图片
image = cv2.imread("D:\\study\\jimei.jpg")
#设置添加椒盐噪声的数目比例
s_vs_p = 0.5
#设置添加噪声图像像素的数目
amount = 0.04
noisy_img = np.copy(image)
#添加salt噪声
num_salt = np.ceil(amount * image.size * s_vs_p)
#设置添加噪声的坐标位置
coords = [np.random.randint(0,i - 1, int(num_salt)) for i in image.shape]
noisy_img[coords[0],coords[1],:] = [255,255,255]
#添加pepper噪声
num_pepper = np.ceil(amount * image.size * (1. - s_vs_p))
#设置添加噪声的坐标位置
coords = [np.random.randint(0,i - 1, int(num_pepper)) for i in image.shape]
noisy_img[coords[0],coords[1],:] = [0,0,0]
#保存图片
cv2.imwrite("noisy_img.png",noisy_img)
实验结果
实验结果
椒盐噪声就是给图片添加黑白噪点,椒指的是黑色的噪点(0,0,0),盐指的是白色的噪点(255,255,255),通过设置amount来控制添加噪声的比例,值越大添加的噪声越多,图像损坏的更加严重。
本实验添加噪声图像像素的数目amount = 0.04。因为椒盐噪声随机出现在图像中的任意位置,所以要设置添加噪声的坐标位置。不仅椒盐噪声的位置是随机的,噪声是黑色的还是白色同样是随机的,所以还要确定噪声的种类。
噪声图像及其直方图
下图是几种常见的噪声PDF特性的测试图案及其直方图。

对于椒盐噪声示例的直方图在密度标度的白端有一个额外的尖峰,因为噪声分量为纯黑或纯白,并且在测试图案中最亮的分量(圆)是亮灰度。除了少许亮度不同外,在图5.4中很难区别出前5幅图像有什么显著不同,即使直方图由明显的区别。
由脉冲噪声污染的图像的椒盐噪声的外观是唯一一种引起退化的、视觉上可区分的噪声类型。
周期噪声
周期噪声是在图像获取中从电力或机电干扰中产生的,是唯一的一种空间依赖型噪声。
周期噪声可通过频率域滤波来显著地减少。
空间上表现为周期性,在频域中是孤立的点,因此常用频域的办法来滤除周期噪声。
噪声参数估计
典型的周期噪声参数是通过检测图像的频谱来进行估计的,但这仅仅适用于非常简单的情况。
通常采用的方法是截取一组“平坦”环境的图像,通过这部分图像的直方图形状与上节中几种典型噪声的直方图形状进行匹配,若形状是高斯,那么我们就说这个噪声是高斯噪声,继续计算它的均值和方差,得到需要的参数。
对于其他噪声,如瑞利、指数等,其参数a和b可以根据均值和方差计算得到。
5.3 只存在噪声的复原——空间滤波
当在一幅图像中唯一存在的退化是噪声时:
![]()
![]()
噪声项是未知的,从g(x,y)或G(u,v)中减去它们不是现实的选择。
在周期噪声的情况下,由G(u,v)的谱来估计N(u,v)通常是可能的,即从G(u,v)中减去N(u,v)可得到原图像的一个估计。
当仅有加性噪声存在时,可以选择空间滤波方法。在这一特殊情况下,图像增强和复原几乎是不可区别。
5.3.1 均值滤波器
-
算术均值滤波器:均值滤波平滑一幅图像的局部变化,虽然模糊了结果,但降低了噪声。用工具箱函数w = fspecial(‘average’, [m, n])和f = imfilter(g, w)实现。
-
几何均值滤波器:丢失更少的图像细节。该非线性滤波器用函数gmean实现。
-
谐波均值滤波器:对盐粒噪声的效果更好,不适用于“胡椒”噪声,它善于处理像高斯噪声那样的其他噪声。该非线性滤波器用函数harmean实现。
-
逆谐波均值滤波器:当Q为正值时,该滤波器消除胡椒噪声;当Q为负数时,该滤波器消除盐粒噪声。但不能同时消除这两种噪声。该非线性滤波器用函数charmean实现。
5.3.2 统计排序滤波器
-
中值滤波器:它可以提供良好的去噪能力,且与相同尺寸的线性平滑滤波器相比引起的模糊更少,应用非常普遍。用工具箱函数medfilt2:f = medfilt2(g, [m, n], ‘symmetric’)实现。
-
最大值和最小值滤波器:最大值滤波器适用于胡椒噪声,最小值滤波器适用于盐粒噪声。使用工具箱函数imdilate和imerode实现。
-
中点滤波器:最适合于处理随机分布的噪声,如高斯噪声或均匀噪声。由最大、最小滤波器结果之和的0.5倍实现。
-
修正的阿尔法均值滤波器:当d=0时,退化为算术均值滤波器;当d=mn-1则退化为中值滤波器;当d取其他值时,适合于处理如混合有高斯噪声和椒盐噪声的多种噪声。使用函数alphatrim实现。
5.3.3 自适应滤波器
自适应局部降低噪声滤波器
随机变量最简单的统计度量是均值和方差,这些适当的参数是自适应滤波器的基础。因为它们是与图像状态紧密相关的数据。均值给出了计算均值的区域中灰度平均值的度量,而方差给出了这个区域的平均对比度的度量。
滤波器作用于局部区域Sxy。滤波器在该区域中心任意一点(x,y)上的响应基于以下4个量:
- g(x, y)表示噪声图像在点(x, y)上的值
- 干扰f(x, y)以形成g(x, y)的噪声方差
- 在Sxy上像素点的局部均值
- 在Sxy上像素点的局部方差
我们希望滤波器性能如下:
1.如果 δ2η为零,则滤波器应该简单地返回g(x,y)的值。这无关紧要,在零噪声情况下g(x,y)等于f(x,y)。
2.如果局部方差与δ2η是高度相关的,则滤波器返回g(x,y)的一个近似值。高局部方差通常与边缘相关,并且应该保护这些边缘。
3.如果两个方差相等,我们则希望滤波器返回Sxy中的像素的算术均值。这种情况发生在局部区域与整个图像有相同特性的条件下,并且局部噪声将通过简单地求平均值来降低。
自适应中值滤波器
中值滤波器,只要脉冲噪声的空间密度不大,性能就会很好(根据经验,Pa和Pb小于 0.2)。自适应中值滤波可以处理具有更大概率的脉冲噪声。
自适应中值滤波器的另一个优点是平滑非脉冲噪声时试图保留细节,这是传统中值滤波器所做不到的。
自适应中值滤波器也工作于矩形窗口区域Sxy内。不同的是自适应中值滤波器在进行滤波处理时会根据某些条件而改变(或增大)Sxy的尺寸。
在模板窗口Sxy定义的滤波器区域内定义如下变量:
- Zmin=min(Sxy),模板窗口Sxy中的最小灰度值
- Zmax=max(Sxy),模板窗口Sxy中的最大灰度值
- Zmed=med(Sxy),模板窗口Sxy中的灰度值的中值
- Zxy,坐标(x,y)处的灰度值
- Smax,Sxy允许的最大尺寸
进程A:
A1=Zmed-Zmin
A2=Zmed-Zmax
如果A1>0且A2<0,则转至进程B
否则增大窗口尺寸
如果窗口尺寸<=Smax,则重复进程A
否则输出Zmed
进程B:
B1=Zxy-Zmin
B2=Zxy-Zmax
如果B1>0且B2<0,则输出Zxy
否则输出Zmed
理解该算法的关键在于,要记住它有3个主要目的:去除椒盐(脉冲)噪声,平滑其他非脉冲噪声,并减少诸如物体边界细化或粗化等失真。值zmin和zmax在算法统计上认为是类脉冲噪声成分,即使它们在图像中并不是最低最高的可能像素值,进程A的目的是确定中值滤波器的输出zmed是否是一个脉冲,进程B的目的是确定zmed非脉冲以后进行中值排序。
实验之Python实现自适应中值滤波法去除椒盐噪声
本实验将原图转化成灰度图,加入椒盐噪声后,用自适应中值滤波法实现去除椒盐噪声。
代码如下:
import cv2
import numpy as np
from PIL import Image
cv2.waitKey(0)
#添加椒盐噪声
def AddNoise(imarray, probility=0.05, method="salt_pepper"): # 灰度图像
#获取图片的长和宽
height, width = imarray.shape[:2]
for i in range(height):
for j in range(width):
if np.random.random(1) < probility: # 随机加盐或者加椒
if np.random.random(1) < 0.5:
imarray[i, j] = 0
else:
imarray[i, j] = 255
return imarray
#中值滤波法
def medianBlur(image, ksize=2 ):
'''
中值滤波,去除椒盐噪声
args:
image:输入图片数据,要求为灰度图片
ksize:滤波窗口大小
return:
中值滤波之后的图片
'''
rows, cols = image.shape[:2]
# 输入校验
half = ksize // 2
startSearchRow = half
endSearchRow = rows - half - 1
startSearchCol = half
endSearchCol = cols - half - 1
dst = np.zeros((rows, cols), dtype=np.uint8)
# 中值滤波
for y in range(startSearchRow, endSearchRow):
for x in range(startSearchCol, endSearchCol):
window = []
for i in range(y - half, y + half + 1):
for j in range(x - half, x + half + 1):
window.append(image[i][j])
# 取中间值
window = np.sort(window, axis=None)
if len(window) % 2 == 1:
medianValue = window[len(window) // 2]
else:
medianValue = int((window[len(window) // 2] + window[len(window) // 2 + 1]) / 2)
dst[y][x] = medianValue
return dst
#自适应中值滤波法
def amp_medianBlur(img, ksize=2 ):
# 图像边缘扩展
#为保证边缘的像素点可以被采集到,必须对原图进行像素扩展。
#一般设置的最大滤波窗口为7,所以只需要向上下左右各扩展3个像素即可采集到边缘像素。
m,n = img.shape[:2]
Nmax = 3
imgn = np.zeros((m + 2 * Nmax, n + 2 * Nmax),dtype=np.uint8)
imgn[ Nmax : (m + Nmax ) , Nmax : (n + Nmax ) ] = img[:,:,0].copy() # 将原图覆盖在imgn的正中间
# 下面开始向外扩展,即把边缘的像素向外复制
imgn[0: Nmax, Nmax: n + Nmax]=img[0: Nmax, 0 : n,0].copy() # 扩展上边界
imgn[0: m + Nmax, n + Nmax : n + 2 * Nmax]=imgn[0: m+Nmax, n: n + Nmax].copy() # 扩展右边界
imgn[m + Nmax: m + 2 * Nmax, Nmax : n + 2 * Nmax]=imgn[m : m + Nmax,Nmax : n + 2 * Nmax].copy() #扩展下边界
imgn[0: m + 2 * Nmax,0: Nmax]=imgn[0: m + 2 * Nmax,Nmax : 2 * Nmax].copy() # 扩展左边界
re = imgn.copy() # 扩展之后的图像
# 得到不是噪声点的中值
for i in range(Nmax,m+Nmax+1):
for j in range(Nmax,n+Nmax+1):
r = 1 # 初始向外扩张1像素,即滤波窗口大小为3
while r!=Nmax+1: #当滤波窗口小于等于7时(向外扩张元素小于4像素)
W = imgn[i - r-1:i + r,j - r-1: j + r].copy()
Imin,Imax = np.min(W),np.max(W) # 最小灰度值 # 最大灰度值
# 取中间值
window = np.sort(W, axis=None)
if len(window) % 2 == 1:
Imed = window[len(window) // 2]
else:
Imed = int((window[len(window) // 2] + window[len(window) // 2 + 1]) / 2)
if Imin < Imed and Imed < Imax: # 如果当前窗口中值不是噪声点,那么就用此次的中值为替换值
break;
else:
r = r + 1; #否则扩大窗口,继续判断,寻找不是噪声点的中值
# 判断当前窗口内的中心像素是否为噪声,是就用前面得到的中值替换,否则不替换
if Imin < imgn[i, j] and imgn[i, j] < Imax: # 如果当前这个像素不是噪声,原值输出
re[i, j] = imgn[i, j].copy()
else: # 否则输出邻域中值
re[i, j] = Imed
return re
#读取图片
image = cv2.imread("D:\\study\\1.png")
width = image.shape[0]
height = image.shape[1]
grayimg = np.zeros([width,height,1],np.uint8)
for i in range(height):
for j in range(width):
grayimg[i,j] = 0.299 * image[i,j][0] + 0.587 * image[i,j][1] + 0.114 * image[i,j][2]
cv2.imshow('srcImage', image)
cv2.imshow('grayImage', grayimg)
img_addnoise = AddNoise(grayimg)
cv2.imshow('addnoise_Image', img_addnoise)
#remig2 = amp_medianBlur(img_addnoise)
#cv2.imshow('re_Image2', remig2)
reimg = medianBlur(img_addnoise)
cv2.imshow('re_Image', reimg)
cv2.waitKey(0)
实验结果分析:
图1为原图,图2为灰度图,图3为添加了椒盐噪声的图,图4为用自适应中值滤波法实现去除椒盐噪声的图。对比原图的灰度图和去除噪声后的复原图,后者虽去除了噪点,也是无法达到百分百的还原成原图。
5.4 用频率波消除周期噪声
用频率域技术可以有效地分析并滤除周期噪声,为消除这些周期噪声,将使用三种类型的选择性滤波器:带阻、带通和陷波滤波器。
-
带阻滤波器:它的主要应用之一是在频率域噪声成分的一般位置近似一直的应用中消除噪声。
理想、巴特沃斯和高斯带阻滤波器表达式如下表:
滤波器的透视图如下:
带阻滤波器的主要应用之一是在频率域噪声分量的一般位置近似已知的应用中消除噪声。如下图1所示,被正弦噪声污染的图像,噪声分量可看成是下图2中的傅里叶频谱中对称的亮点对,而且噪声分量位于关于变换原点的近似圆上,因此可使用圆对称带阻滤波器,如下图3所示(4阶的巴特沃斯带阻滤波器),通过设置适当的半径和宽度,其完全包围了噪声脉冲,并且带组滤波中通常要求尖锐的窄滤波器以保持更多的细节,结果如下图4所示:

-
带通滤波器:它执行与带阻滤波器相反的操作。但是通常不会在一幅图像上直接执行带通滤波【会消除太多的图像细节】。然而带通滤波在一幅图像中屏蔽选中频段导致的效果非常有用。
我们可以在上图1上应用与带阻滤波器相对应的带通滤波器然后取带通滤波变换的反变换,得到上图1中的噪声图案,如下图所示:
-
陷波滤波器:阻止(或通过)事先定义的中心频率邻域内的频率。
如下图所示,展示了理想、巴特沃斯和高斯陷波带阻滤波器的三维图:
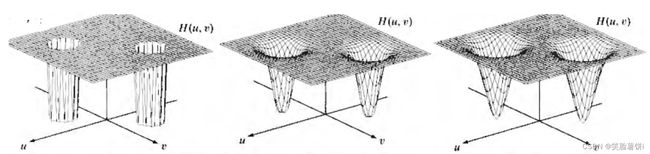
由于傅立叶变换的对称性,陷波滤波器必须以关于原点对称的形式出现【如果陷波滤波器位于原点处陷波滤波器是其本身】。同样,也可以得到陷波带阻滤波器相对应的陷波带通滤波器通过而不是已知陷波区域中所包含频率的陷波滤波器。 -
最佳陷波滤波
当存在几种干扰分量时上面讨论的滤波过程会消除过多的图像细节,而且此时干扰成分通常不是单频脉冲【通常携带干扰模式信息的宽边缘】。这种情况下可应用最佳陷波滤波的方法,第一步屏蔽干扰的主要成分,第二步是从被污染的图像中减去该模式的一个可变的加权部分。
5.5 线性、位置不变的退化
在退化复原模型中,输入输出关系可以表示为:
![]()
如果系统H是一个线性系统,那么H应该满足可加性和均匀性:
![]()
![]()
这里,a是比例常数,f1(x, y)和f2(x, y)是任意两幅输入图像。
在图像中任何一点的响应,只取决于在该点的输入值,而与该点的位置无关。
总之,具有加性噪声的线性空间不变退化系统,可在空间域建模为退化(点扩散)函数与一幅图像的卷积,然后再加上噪声。基于卷积定理,在频率域中,同样的过程可表示为图像和退化函数的变换的乘积,然后再加上噪声的变换。
许多类型的退化可近似为线性、位置不变的过程。这种方法的优点是:可以使用许多线性系统理论的工具来解决图像复原问题。
5.6 估计退化函数
在图像复原中,有3种主要的估计退化函数的方法:观察法、试验法和数学建模法。使用以某种方式估计的退化函数复原一幅图像的过程有时称为盲目去卷积,因为真正的退化函数很少能完全知晓。
5.6.1 图像观察估计法
假设提供了一幅退化图像,而没有退化函数H的知识,那么估计该函数的一个方法就是收集图像自身的信息。例如,如果图像是模糊的,可以观察包含简单节后的一小部分图像,像某一物体和背景的一部分。为了减少观察时的噪声影响,可以寻找强信号的内容区。
5.6.2 试验估计法
如果可以使用与获取退化图像的设备相似的装置,理论上可以得到一个准确的退化估计是可能的。与退化图像类似的图像可以通过各种系统装置得到,退化这些图像使其尽可能接近希望复原的图像。利用相同的系统设置,由成像一个脉冲得到退化的冲击响应。
5.6.3 模型估计法
由于退化模型可解决图像复原问题,因此多年来一直在应用。在某些情况下,模型要把引起退化的环境因素考虑在内。
图像模糊可以使用工具箱函数fspecial来建模:PSF = fspecial(‘motion’, len, theta);调用fspecial将返回PSF,该PSF用来近似摄像机线性移动len个像素的效果。
使用函数imfilter来创建一幅已知PSF的退化图像:g = imfilter(f, PSF, ‘circular’);其中circular用来减少边缘效应。
然后通过g = g + noise;添加适当的噪声来完成退化图像的模糊。
5.7 逆滤波
在该方法中,用退化函数除退化图像的傅里叶变换来计算原始图像的傅里叶变换估计。如果退化是零或非常小的值,N(u, v)/H(u,v)之比很容易决定估计值。一种解决退化是零或者很小值问题的途径是限制滤波的频率使其接近原点值。
5.8 最小均方误差(维纳)滤波
对于运动引起的图像模糊,最简单的方法是直接做逆滤波,但是逆滤波对加性噪声特别敏感,使得恢复的图像几乎不可用(通过实验可知)。经过研究提出了一些改进方法,其中之一就是最小均方差滤波。
维纳滤波也叫最小均方误差滤波,是一种建立在最小化统计准则的基础上的复原方法,在平均意义上,它可以看成是最优的。
维纳滤波综合了退化函数和噪声统计特征两个方面进行复原处理,在认为图像和噪声是随机过程的基础上,以恢复图像和原图像的均方误差最小为准则。
最小均方差(维纳)滤波用来去除含有噪声的模糊图像,其目标是找到未污染图像的一个估计,使它们之间的均方差最小,可以去除噪声,同时清晰化模糊图像。
维纳滤波的实质就是:一个复数量与其共轭的乘积等于该复数量幅度的平方。
实验之用维纳滤波去除运动引起的图像模糊
代码如下:
import matplotlib.pyplot as plt
import numpy as np
from numpy import fft
import math
import cv2
# 仿真运动模糊
def motion_process(image_size, motion_angle):
PSF = np.zeros(image_size)
print(image_size)
center_position = (image_size[0] - 1) / 2
print(center_position)
slope_tan = math.tan(motion_angle * math.pi / 180)
slope_cot = 1 / slope_tan
if slope_tan <= 1:
for i in range(15):
offset = round(i * slope_tan) # ((center_position-i)*slope_tan)
PSF[int(center_position + offset), int(center_position - offset)] = 1
return PSF / PSF.sum() # 对点扩散函数进行归一化亮度
else:
for i in range(15):
offset = round(i * slope_cot)
PSF[int(center_position - offset), int(center_position + offset)] = 1
return PSF / PSF.sum()
# 对图片进行运动模糊
def make_blurred(input, PSF, eps):
input_fft = fft.fft2(input) # 进行二维数组的傅里叶变换
PSF_fft = fft.fft2(PSF) + eps
blurred = fft.ifft2(input_fft * PSF_fft)
blurred = np.abs(fft.fftshift(blurred))
return blurred
def inverse(input, PSF, eps): # 逆滤波
input_fft = fft.fft2(input)
PSF_fft = fft.fft2(PSF) + eps # 噪声功率,这是已知的,考虑epsilon
result = fft.ifft2(input_fft / PSF_fft) # 计算F(u,v)的傅里叶反变换
result = np.abs(fft.fftshift(result))
return result
def wiener(input, PSF, eps, K=0.01): # 维纳滤波,K=0.01
input_fft = fft.fft2(input)
PSF_fft = fft.fft2(PSF) + eps
PSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + K)
result = fft.ifft2(input_fft * PSF_fft_1)
result = np.abs(fft.fftshift(result))
return result
def normal(array):
array = np.where(array < 0, 0, array)
array = np.where(array > 255, 255, array)
array = array.astype(np.int16)
return array
def main(gray):
channel = []
img_h, img_w = gray.shape[:2]
PSF = motion_process((img_h, img_w), 60) # 进行运动模糊处理
blurred = np.abs(make_blurred(gray, PSF, 1e-3))
result_blurred = inverse(blurred, PSF, 1e-3) # 逆滤波
result_wiener = wiener(blurred, PSF, 1e-3) # 维纳滤波
blurred_noisy = blurred + 0.1 * blurred.std() * \
np.random.standard_normal(blurred.shape) # 添加噪声,standard_normal产生随机的函数
inverse_mo2no = inverse(blurred_noisy, PSF, 0.1 + 1e-3) # 对添加噪声的图像进行逆滤波
wiener_mo2no = wiener(blurred_noisy, PSF, 0.1 + 1e-3) # 对添加噪声的图像进行维纳滤波
channel.append((normal(blurred),normal(result_blurred),normal(result_wiener),
normal(blurred_noisy),normal(inverse_mo2no),normal(wiener_mo2no)))
return channel
if __name__ == '__main__':
image = cv2.imread('D:\\Study\\1.png')
b_gray, g_gray, r_gray = cv2.split(image.copy())
Result = []
for gray in [b_gray, g_gray, r_gray]:
channel = main(gray)
Result.append(channel)
blurred = cv2.merge([Result[0][0][0], Result[1][0][0], Result[2][0][0]])
result_blurred = cv2.merge([Result[0][0][1], Result[1][0][1], Result[2][0][1]])
result_wiener = cv2.merge([Result[0][0][2], Result[1][0][2], Result[2][0][2]])
blurred_noisy = cv2.merge([Result[0][0][3], Result[1][0][3], Result[2][0][3]])
inverse_mo2no = cv2.merge([Result[0][0][4], Result[1][0][4], Result[2][0][4]])
wiener_mo2no = cv2.merge([Result[0][0][5], Result[1][0][5], Result[2][0][5]])
#========= 可视化 ==========
plt.figure(1)
plt.xlabel("Original Image")
plt.imshow(np.flip(image, axis=2)) # 显示原图像
plt.figure(2)
plt.figure(figsize=(8, 6.5))
imgNames = {"Motion blurred":blurred,
"inverse deblurred":result_blurred,
"wiener deblurred(k=0.01)":result_wiener,
"motion & noisy blurred":blurred_noisy,
"inverse_mo2no":inverse_mo2no,
'wiener_mo2no':wiener_mo2no}
for i,(key,imgName) in enumerate(imgNames.items()):
plt.subplot(231+i)
plt.xlabel(key)
plt.imshow(np.flip(imgName, axis=2))
plt.show()
实验结果如下:
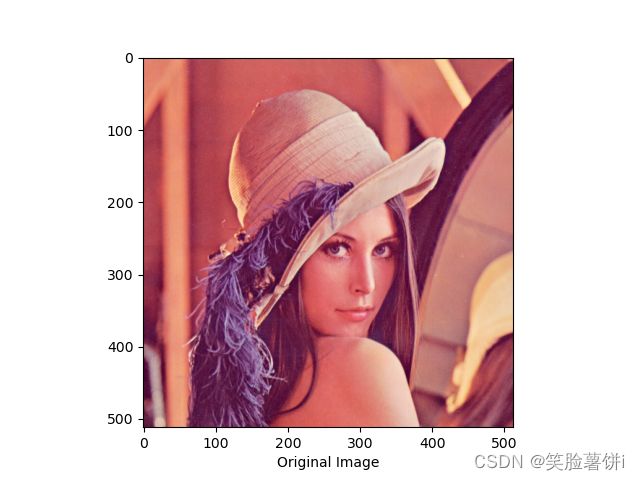

实验结果分析:
由实验结果可知,与直接逆滤波相比,当有运动噪声和随机噪声同时存在维纳滤波的处理效果优势明显,对噪声的过滤性能优越。
当只有运动噪声时,如果k只选取不当,维纳滤波的优越性难以体现。
因此可以发现维纳滤波的缺点就是难以靠数学分析发现最合适的k值,需要手工交互选取合适的k值,这个可以通过约束最小二乘方滤波。
5.9 约束最小二乘方滤波
约束最小二乘方滤波的核心是H对噪声的敏感性问题。减少噪声敏感新问题的一种方法是以平滑度量的最佳复原为基础的,建立下列约束条件:
这里,![]() 是为退化图像的估计,N为加性噪声,拉普拉斯算子
是为退化图像的估计,N为加性噪声,拉普拉斯算子![]() 在这里表示平滑程度。
在这里表示平滑程度。
推导:
将上式表示成矩阵形式,同时将约束项转换成拉格朗日乘子项:
![]()
最小化上代价函数,对![]() 求导,令等零有
求导,令等零有![]()
5.10 几何均值滤波
使用几何均值滤波器复原图像,复原图像![]() 在点 ( x , y ) (x,y)(x,y) 的值是邻域中的像素的几何平均值:
在点 ( x , y ) (x,y)(x,y) 的值是邻域中的像素的几何平均值:
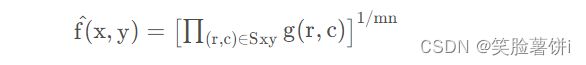
代码如下:
# 几何均值滤波器 (Geometric mean filter)
img = cv2.imread("../images/Fig0507b.tif", 0) # flags=0 读取为灰度图像
img_h = img.shape[0]
img_w = img.shape[1]
# 算术平均滤波 (Arithmentic mean filter)
kSize = (3,3)
kernalMean = np.ones(kSize, np.float32) / (kSize[0]*kSize[1]) # 生成归一化盒式核
imgAriMean = cv2.filter2D(img, -1, kernalMean)
# 几何均值滤波器 (Geometric mean filter)
m, n = 3, 3
order = 1/(m*n)
kernalMean = np.ones((m,n), np.float32) # 生成盒式核
hPad = int((m-1) / 2)
wPad = int((n-1) / 2)
imgPad = np.pad(img.copy(), ((hPad, m-hPad-1), (wPad, n-wPad-1)), mode="edge")
imgGeoMean = img.copy()
for i in range(hPad, img_h + hPad):
for j in range(wPad, img_w + wPad):
prod = np.prod(imgPad[i-hPad:i+hPad+1, j-wPad:j+wPad+1]*1.0)
imgGeoMean[i-hPad][j-wPad] = np.power(prod, order)
plt.figure(figsize=(9, 6))
plt.subplot(131), plt.axis('off'), plt.title("Original")
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.subplot(132), plt.axis('off'), plt.title("Arithmentic mean filter")
plt.imshow(imgAriMean, cmap='gray', vmin=0, vmax=255)
plt.subplot(133), plt.axis('off'), plt.title("Geometric mean filter")
plt.imshow(imgGeoMean, cmap='gray', vmin=0, vmax=255)
plt.tight_layout()
plt.show()
实验结果如下:

实验结果分析:几何均值滤波器实现的平滑与算术平均滤波器相当,但损失的图像细节更少。
5.11 由投影重建图像
5.11.1 引言
假设我们要用一束细细的,平行的X射线从左到右穿过(通过一个图像平面),这里我们假设物体吸收的射线束能量 比背景吸收的射线束能量多。我们利用放在放在另一端的X射线吸收检测器来检测射线通过这个物体的能量
所以当左侧有一排X射线(光束带),右侧有一排X射线检测器(检测器带/吸收剖面)的时候,就会形成一副函数图像(通过接收器的位置和应该接收点接收能量的离散值形成),我们的目的是为了复原X射线穿过物体的图像,但是只是知道这个函数有什么用呢?
反投影法
我们需要基于上述函数的信息来重建一幅图像,如下方右侧的图像所示,我们沿着射线来的方向把一维信号反投影回去。穿过二维图像的一维信号的反投影过程,可想象为把投影穿过该区域反“涂抹”回去。

反投影复原出二维图像
利用上面描述的反投影法,刚才显示的图片是角度为 0 时得到的反投影图像,下面我们把角度旋转45度再进行一次,得到结果反投影结果如下图所示:

继续进行X射线带和检测带的45度角旋转,得到 0° ,45° ,90° ,135° 的四个角度(没有180° 是因为它的反投影会和0° 重合,导致得出的图像出现误差),如下图左所示他已经稍微可以看出来一些是原来的图像了。
以此为理论依据,我们把旋转的角度变小,设置为间隔为 5.625° ,结果如下右图所示,基本可以还原出物体的轮廓,但是间隔不能设置的太小,间隔越小导致图像越模糊,这也就需要之后我们进一步处理图像,使该物体让人们看起来更舒服。
5.11.2 计算机断层(CT)原理
刚才提到了,使用反投影技术(比如32个以5.625°为间隔的反投影),可以还原一个二维的图像,但是我们希望得到一个三维的图像,所以我们三维面叠加若干个二维图像,得到三维的物体模型。
这里详细说明一下,为了得到一个二维图像切面,所以刚才我们在水平面上进行了32个以5.625°为间隔的旋转,通过32个反投影的叠加得到二维图像切面。之后我们在竖直平面翻转32个以5.625°为间隔的旋转,每一次翻转都得到了一个二维图像切面,通过叠加这些二维图像,获得三维物体。
第一代CT和第二代CT,工作原理相同,只是第二代CT 发射扇形的射线束。第三代CT和第四代CT就发展为不需平移的了,只需要射线旋转,使用了足够长的检测带,第四代则是使用了环形的1检测带,三代和四代CT优点是速度快,但是造价偏高。 第五代往后的CT就不在陈述了。
5.11.3 投影和雷登变换
在笛卡尔坐标系中,一条直线可以用斜截式 : y=ax+b 来表示,在投影这方面,我们需要用到它的法线表达式: ![]()
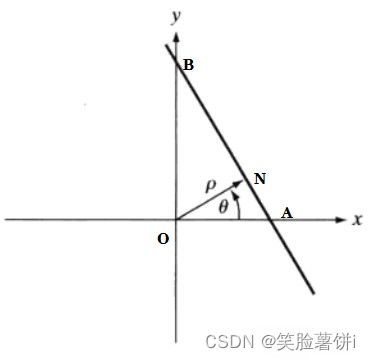
雷登变换:
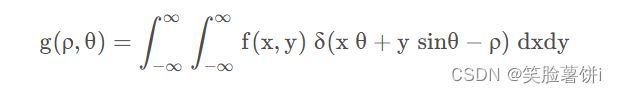
雷登变换是投影重建的基石。
5.11.4 傅里叶切片定理

其中F(u,v)就表示f(x,y )的二维傅里叶变换。如下图所示,任意一个一维的投影的一维傅里叶变换可沿着一个角度提取一条线的F(u,v)值得到,反过来说,在二维傅里叶变换中选一个角度原点画的这个直线进行反傅里叶变换就是一维投影。