JAVA-高频面试题汇总:数组(下)
前言
为了让小伙伴们更好地刷题,我将所有leetcode常考题按照知识点进行了归纳。
高频题汇总:
JAVA-高频面试题汇总:动态规划
JAVA-高频面试题汇总:字符串
JAVA-高频面试题汇总:二叉树(上)
JAVA-高频面试题汇总:二叉树(下)
JAVA-高频面试题汇总:回溯
JAVA-高频面试题汇总:链表
JAVA-高频面试题汇总:数组(上)
JAVA-高频面试题汇总:数组(下)
接下来还会进行其他模块的总结,有一起在准备暑期实习的JAVA后端的伙伴可以一起交流!
小编微信: Apollo___quan
目录
- 数组中数字出现的次数(剑指)
- 数组中数字出现的次数 II(剑指)
- 和为s的连续正数序列(剑指)
- 和为s的两个数字(剑指)
- 数组中重复的数字(剑指)
- 构建乘积数组(剑指)
- 三数之和
- 四数之和
- 二进制中1的个数(剑指))
- 不用加减乘除做加法(剑指)
- 求1+2+…+n(剑指)
11.数组中数字出现的次数(剑指)
思路
1.将所有数异或,会剩下两个数,其他数相消。0^0=0; 0^1=1; 1^0=1; 1^1=0。
2.剩下两个数区分不出,所以需要将两个数分在不同的组,两组各得出一个。
3.先得出这两个数某一位数不同,然后根据这个进行分组。
class Solution {
public int[] singleNumbers(int[] nums) {
//用于将所有的数异或起来
int k = 0;
for(int num: nums) {
k ^= num; //k即为剩下的两个数的异或
}
//获得k中最低位的1
int mask = 1;
while((k & mask) == 0) { //对k进行位与,与0001,0010,0100这样子与,得到非0时即为不同的位,根据此将两个数分到不同组
mask <<= 1;
}
int a = 0;
int b = 0;
for(int num: nums) {
if((num & mask) == 0) {
a ^= num; //分组1进行异或后得到a
} else {
b ^= num; //分组2进行异或后得到b
}
}
return new int[]{a, b};
}
}
12.数组中数字出现的次数 II(剑指)
1.遍历数组,记录所有数字的每一位出现次数,并对3求余,便可知道哪些位只出现了1次
2.根据这些位还原出数字
时间复杂度 O(N) : 其中 NN位数组 nums的长度;遍历数组占用O(N) ,每轮中的常数个位运算操作占用 O(1)。
空间复杂度 O(1) : 数组 counts长度恒为 32 ,占用常数大小的额外空间。
class Solution {
public int singleNumber(int[] nums) {
int[] counts = new int[32]; //int一共4字节,32位
for(int num : nums) {
for(int j = 0; j < 32; j++) {
counts[j] += num & 1; //记录每个数字的每一位出现次数
num >>>= 1;
}
}
int res = 0;
for(int i = 0; i < 32; i++) {
res <<= 1;
res |= counts[31 - i] % 3; //还原出数字
}
return res;
}
}
13.和为s的连续正数序列(剑指)
思路
滑动窗口(双指针)
class Solution {
public int[][] findContinuousSequence(int target) {
int i = 1, j = 2, s = 3; //初始化i、j最左相邻
List<int[]> res = new ArrayList<>();
while(i < j) {
if(s == target) { //若等于目标值
int[] ans = new int[j - i + 1]; //创建新数组记录下此时窗口中的值
for(int k = i; k <= j; k++)
ans[k - i] = k;
res.add(ans); //将数组加入res
}
if(s >= target) { //大于等于目标值时
s -= i; //从s中减去i
i++; //窗口左边界移动
} else {
j++; //小于目标值时右边界右移
s += j;
}
}
return res.toArray(new int[0][]);
}
}
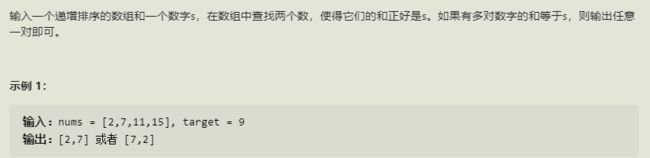
14.和为s的两个数字(剑指)
思路
和上一题相区别,滑动窗口是两个指针一起从左往右,该题为一左一右往中间
class Solution {
public int[] twoSum(int[] nums, int target) {
int i = 0, j = nums.length - 1; //初始化i最左,j最右,与上一题区别
while(i < j) {
int s = nums[i] + nums[j];
if(s < target) i++; //小于target则i右移
else if(s > target) j--; //大于target则j左移
else return new int[] { nums[i], nums[j] };
}
return new int[0]; //若都没有输出空数组[],元素个数为0个,实际在内存开空间了,但大小为0
}
}
15.数组中重复的数字(剑指)
思路
原地置换
如果没有重复数字,那么正常排序后,数字i应该在下标为i的位置,所以思路是重头扫描数组,遇到下标为i的数字如果不是i的话,(假设为m),那么我们就拿与下标m的数字交换。在交换过程中,如果有重复的数字发生,那么终止返回
时间复杂度O(N)
空间复杂度O(1)
class Solution {
public int findRepeatNumber(int[] nums) {
int temp;
for(int i=0;i<nums.length;i++){
while (nums[i]!=i){ //遇到不对应的数
if(nums[i]==nums[nums[i]]){
return nums[i];
}
temp=nums[i]; //交换两个数,进入下一次循环(判断交换后的新nums[i]是否等于i)
nums[i]=nums[temp];
nums[temp]=temp;
}
}
return -1;
}
}
16.构建乘积数组(剑指)
思路
根据表格的主对角线(全为 11 ),可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积,即可 不使用除法 就获得结果。
class Solution {
public int[] constructArr(int[] a) {
if(a.length == 0) return new int[0]; //返回空数组
int[] b = new int[a.length];
b[0] = 1;
int tmp = 1;
for(int i = 1; i < a.length; i++) { //上三角,从第二行(i=1)开始遍历到第五行(i=4)
b[i] = b[i - 1] * a[i - 1];
}
for(int i = a.length - 2; i >= 0; i--) { //下三角,从第四行(i=3)遍历到第一行(i=0)
tmp *= a[i + 1];
b[i] *= tmp;
}
return b;
}
}
17.三数之和
思路
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for(int k = 0; k < nums.length - 2; k++){
if(nums[k] > 0) break; //最小的大于0,加上后面的肯定也>0
if(k > 0 && nums[k] == nums[k - 1]) continue; //跳过相同的nums[k]
int i = k + 1, j = nums.length - 1;
while(i < j){
int sum = nums[k] + nums[i] + nums[j];
if(sum < 0){
while(i < j && nums[i] == nums[++i]); //太小i右移
} else if (sum > 0) {
while(i < j && nums[j] == nums[--j]); //太大j左移
} else {
res.add(new ArrayList<Integer>(Arrays.asList(nums[k], nums[i], nums[j])));
while(i < j && nums[i] == nums[++i]); //相等则加入res,i右移j左移
while(i < j && nums[j] == nums[--j]);
}
}
}
return res;
}
}
18.四数之和
思路
四数之和与前面三数之和的思路几乎是一样的,这里其实就是在前面的基础上多添加一个遍历的指针而已。
使用四个指针(a
遇时,表示以当前的a和b为最小值的解已经全部求得。b++,进入下一轮循环b循环,当b循环结束后。
a++,进入下一轮a循环。 即(a在最外层循环,里面嵌套b循环,再嵌套双指针c,d包夹求解)。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for(int k = 0; k < nums.length - 3; k++){
if(nums[k] + nums[k+1] + nums[k+2] +nums[k+3] > target){ //这里和三数之和重点区别
break;
}
if(k > 0 && nums[k] == nums[k - 1]) continue; //跳过k相同的,注意k>0条件,说明不是第一次遇到
for(int h = k + 1; h < nums.length - 2; h++){
if(h > (k + 1) && nums[h] == nums[h - 1]) continue;//跳过h相同的,注意h > (k + 1)条件,说明不是第一次遇到
int i = h + 1, j = nums.length - 1;
while(i < j){
int sum = nums[k] + nums[h] + nums[i] + nums[j];
if(sum < target){
while(i < j && nums[i] == nums[++i]); //太小i右移
} else if (sum > target) {
while(i < j && nums[j] == nums[--j]); //太大j左移
} else {
res.add(new ArrayList<Integer>(Arrays.asList(nums[k], nums[h], nums[i], nums[j])));
while(i < j && nums[i] == nums[++i]); //相等则加入res,i右移j左移
while(i < j && nums[j] == nums[--j]);
}
}
}
}
return res;
}
}
19.二进制中1的个数(剑指)
思路
基础题,逐位判断
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res += n & 1;
n >>>= 1;
}
return res;
}
}
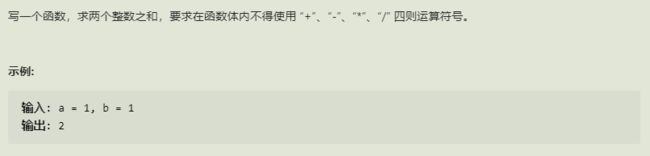
20.不用加减乘除做加法(剑指)
思路
class Solution {
public int add(int a, int b) {
while(b != 0){ //进位为0时跳出循环
int temp = (a & b) << 1; //记录进位
a = a ^ b; //将a换位无进位和
b = temp; //将b换为进位
}
return a;
}
}
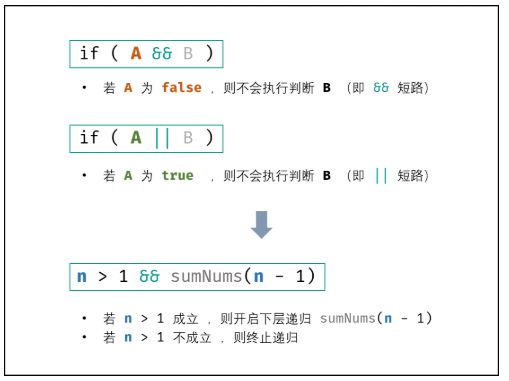
21.求1+2+…+n(剑指)
思路
通过逻辑与操作,A && B,当A不成立时B被短路。
A是递归条件控制递归何时停止,所以n > 1。
B是递归操作,同时B应在A条件下时刻满足,于是sumNums(n - 1) > 0,其中0换成-1等其实也可。
且最终返回的是个boolean类型,这个要注意
class Solution {
int res = 0;
public int sumNums(int n) {
boolean x = n > 1 && sumNums(n - 1) > 0; //最后一次递归n=1,后面的短路,但不影响res累计
res += n; //将每次的n累加
return res;
}
}
总结
数组(下)整理完毕,其余类型
JAVA-高频面试题汇总:动态规划
JAVA-高频面试题汇总:字符串
JAVA-高频面试题汇总:二叉树(上)
JAVA-高频面试题汇总:二叉树(下)
JAVA-高频面试题汇总:回溯
JAVA-高频面试题汇总:链表
JAVA-高频面试题汇总:数组(上)