cuda编程入门07
程序优化技巧
程序解读
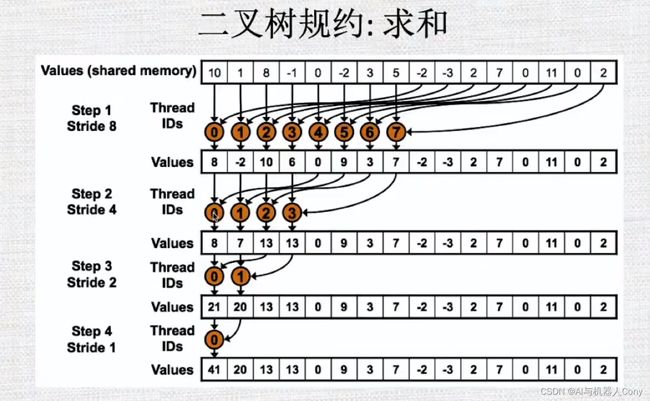
降低256倍,但是后面数组长度还是不知道的
对1万的元素在此降低一定倍数
初始加速比为9.58左右
这里没有volatie
if (tid < 32) sdata[tid] += sdata[tid + 32];
__syncthreads();
在一个wrap内进行合并
sdata[tid] += sdata[tid + 32];
sdata[tid] += sdata[tid + 16];
sdata[tid] += sdata[tid + 8];
sdata[tid] += sdata[tid + 4];
sdata[tid] += sdata[tid + 2];
sdata[tid] += sdata[tid + 1];
加速比变为12
必须使用volitate修饰符
加速比要更快
或者去掉volatile,通过函数调用来实现,加速比变成13.25
cuda程序优化
最大化并行执行
两个向量间的运算容易计算出并行运算
LU不完全分解是一种对矩阵进行分解的方法,旨在将原始矩阵分解成一个下三角矩阵L和一个上三角矩阵U,即 A = L * U。与条件 (Fill-in) 是指在进行LU分解时,为了保持矩阵的稀疏性,在填充0元素的过程中引入的非零元素的数量。因此,与条件越小,矩阵的稀疏性就越好,效率也越高。常见的与条件为lu不完全分解包括:
-
ILU(0):不考虑与条件的影响,只进行矩阵的LU分解,并且保持矩阵的稀疏性。
-
ILU(k):使用一个参数k来控制矩阵的与条件。这种分解方法可以得到比ILU(0)更好的矩阵分解结果。
-
MILU:基于对称不变性的因子分解方法,可以在保证矩阵稀疏性的同时,获得较好的与条件。
-
Crout-ILU:采用Crout分解的方法,通过控制矩阵的填充次序,来实现不同的与条件控制。
-
threshold-ILU:使用阈值方法来控制矩阵的填充次序,从而获得不同的与条件。
这些常见的与条件为LU不完全分解方法可以根据需要进行选择,以满足特定问题的求解要求。
在数值计算中,与条件(Condition Number)是用来描述矩阵或者函数在输入数据微小变化时输出结果的敏感程度的一个数值。在矩阵计算中,通常使用矩阵的谱范数(或2-范数)来定义矩阵的与条件数。
对于一个矩阵A,如果其逆矩阵不存在,则称其为奇异矩阵。此时,我们无法使用标准的求逆矩阵的方法来求解线性方程组 Ax = b。因此,我们需要使用其他求解方法来找到一个近似解x’。
如果矩阵A的条件数很小,说明在输入的b中存在微小的变化时,其对应的解x’的变化也很小,即输入数据的微小扰动对输出结果的影响很小,因此矩阵计算过程中误差较小。相反,如果矩阵A的条件数很大,说明在输入的b中存在微小的变化时,其对应的解x’的变化相对较大,即输入数据的微小扰动对输出结果的影响比较大,因此矩阵计算过程中误差较大。
因此,与条件数是评价矩阵在数值计算中的可靠性与稳定性的重要指标之一。在矩阵计算中,我们通常希望使用具有较小与条件数的矩阵来求解线性方程组,这样可以获得更加稳定和可靠的结果。
天然串行的,该类算法对三角解法进行并行难度非常大。
在设计时候,需要了解算法是并行的还是串行的,理解后根据算法结构能否通过数学手段让算法具有更高的并行性,
设计算法共享内存
线程同步
块间通信
在并行计算中,为了提高系统的性能,通常需要让通信和计算重叠,即在进行计算的同时,尽可能避免因等待通信而浪费时间,或者相反。以下是常用的技巧:
-
Pipelining:将计算过程分为多个阶段,每个阶段对应一个计算任务和一个通信任务,这些任务可以同时执行,从而实现计算和通信的重叠。
-
Message-Passing Protocol:采用异步通信协议,即发送方在发送消息后不需要等待接收方的响应,可以继续进行计算操作,从而实现通信和计算的重叠。
-
Overlapping Communication and Computation (OCC):在计算过程中尽可能地多使用本地存储器,减少内存访问量,同时采用数据的异步预取保证数据在计算之前已经被加载到本地存储器中,从而实现通信和计算的重叠。
-
SIMD机器模式:采用向量寄存器来进行计算,在向量寄存器中的数据可以同时被操作,从而实现计算和通信的重叠。
-
Cacheing:合理地采用本地缓存技术,使得在数据读入之后可以进行多次的操作,从而减少因等待数据而浪费的时间,实现计算和通信的重叠。
这些技巧可以在不同的场景中应用,通过让计算和通信重叠,来提高系统的并行计算效率。
cpu和gpu相互间通信, 同步传输,等待执行完成后再执行, 异步,启动后不管了,往后执行
尽量让每个流多处理器保有更多的块
这句话可以理解为,在CUDA编程中,每个线程块所使用的资源最多只能占据总可用资源的一半。具体来说,CUDA设备包括多个Streaming Multiprocessor(SM),而SM包含多个CUDA核心。每个SM有一个有限的总共享内存、寄存器和线程数等资源。在CUDA程序中,我们需要合理地分配这些资源以实现高效的并行计算。
为了充分利用CUDA设备的资源,我们通常会将任务分割成多个线程块,并在每个线程块中启动多个线程来执行计算任务。然而,在每个线程块中,使用的共享内存、寄存器和线程数等资源也是受限的。因此,为了合理利用CUDA设备的资源,在设计CUDA程序时,需要考虑如何最大限度地利用每个线程块的资源,同时避免超过总可用资源的限制。
因此,根据上述原则,在CUDA编程中,通常需要确保每个线程块所使用的资源最多只占据总共享内存、寄存器和线程数等资源的一半,从而避免线程块之间互相影响,确保CUDA程序的正确性和高效性。这也是CUDA编程中一个重要的优化策略。
这句话的意思是,如果存在多个线程块(blocks)同时运行的情况,并且这些线程块不是都在等待同步(syncthreads())操作,那么多处理器可以保持繁忙状态。这是因为,在CUDA编程中,每个线程块都会被分配到一个Streaming Multiprocessor(SM)上运行,一个SM可以同时运行多个线程块。
当某个线程块需要等待其他线程块才能继续执行时,通常会使用同步操作syncthreads()来等待其他线程块完成工作。在等待期间,该线程块所在的SM可能没有可用的任务,从而导致浪费计算资源。但是,如果存在多个线程块同时运行的情况,即使其中一个线程块在等待同步操作,其它线程块仍然可以继续进行计算,从而使SM保持繁忙状态,提高GPU的利用率和计算效率。
因此,在设计CUDA程序时,我们需要充分利用多处理器的并行计算能力,尽可能避免线程块之间的互相等待,从而保持设备的最大利用率。这也是CUDA编程中的一个重要优化策略。

尽可能32的倍数

设计程序时尽量使 比例为1 当前处于活跃状态/ 最大活跃状态数目
内存优化使用
基本策略
尽量减少内存开销
保证程序可移植
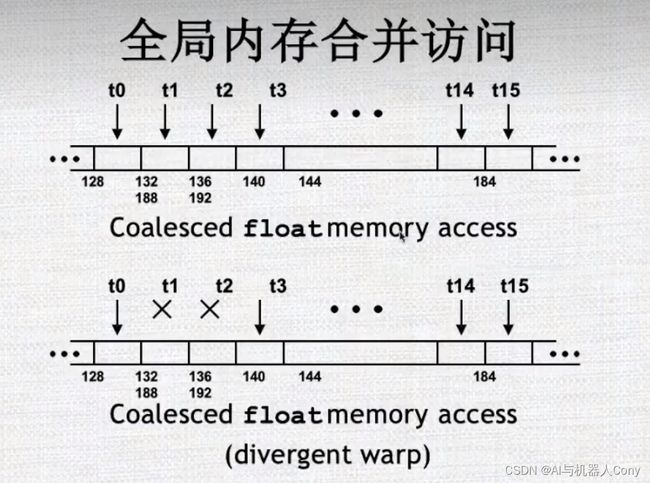
coalesced float memory access 和 divergent warp 都是和CUDA程序中内存访问相关的问题。
coalesced float memory access 指的是在CUDA程序中,当一个线程块中的多个线程需要同时对连续的浮点型数据进行读取或写入时,如果这些线程在内存中访问的地址是连续的,就可以通过合并访问请求,使得设备能够一次性地读取或写入多个相邻的数据块,从而提高程序运行效率。这种一次性读取或写入多个数据块的访问方式称为“内存访问协同(Coalesced Memory Access)”,而相关的内存访问操作称为“协同内存访问”。
但是如果线程块中的不同线程访问的内存地址不是连续的,就会造成内存访问散乱、效率低下的问题。
divergent warp 则指的是,在一个线程块中,每个warp(32个线程构成的一组)内的线程需要同时执行同样的操作。但是,如果某个warp中的线程需要执行不同的操作,比如一个if语句中一部分线程需要执行if分支,另外一部分线程需要执行else分支,这就会导致该warp中的线程发生分歧(divergent),从而影响程序的并行性和计算效率。
因此,在CUDA程序中,为了提高内存访问效率和并行计算效率,需要尽可能地使用协同内存访问,并避免出现线程分歧。这也是CUDA编程中的一项重要优化策略。
misaligned starting address 是指在CUDA程序中,如果一个线程块需要对内存中的某个数据区域进行读写操作,但是该数据区域的起始地址不是按照正确的对齐方式分配的,就会导致访问效率降低和内存访问异常的问题。
在CUDA编程中,为了提高内存访问效率,通常要尽可能地使用对齐的内存访问方式。在大多数计算机系统中,每个数据类型都有一个最小对齐字节数,即该数据类型的大小(以字节数为单位)或缓存行大小(通常是32或64字节)。因此,当从内存中读取一个数据时,该数据的地址应该是这个数据类型的倍数。如果数据的地址没有正确对齐,CPU或GPU需要进行多次内存访问才能读取该数据,从而导致性能损失。
在CUDA程序中,如果数据区域的起始地址没有按照正确的对齐方式分配,就会出现misaligned starting address的问题。解决这个问题的方法是,在程序中使用适当的内存分配函数(比如cudaMallocManaged()或cudaMallocPitch()等),使得分配的内存区域起始地址满足对齐要求。另外,在设计CUDA程序时,还可以通过合理的内存访问策略和对齐方式来提高程序的效率和性能。
不是16的倍数