【算法基础】常数操作 时间复杂度 选择排序 冒泡排序 插入排序 位运算
常数操作
定义
一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作叫做常数操作，比如常见的计算操作：加减乘除。
取出数组中任意位置元素可以叫做常数操作，因为数组的地址是连续的，计算机取的时候可以直接计算出偏移量来读取，但是对于Java中的链表List来说，它必须从第一个位置开始，一个一个往后取，因为前一个元素存储着后一个元素的地址，链表的地址是不连续的。
//常数操作
int a = arr[i];
//非常数操作
int b = list.get(i);时间复杂度
定义
时间复杂度是用来衡量算法的执行时间的一个概念。它描述了算法的时间耗费与输入规模的增长关系，通常用称为大O记法的符号表示。大O符号表示算法运行时间的上限，即当输入规模 n 趋近无穷大时，算法运行时间在最坏情况下的增长率。
公式
时间复杂度：在常数操作表达式中，不要低阶项最要最高阶项，并省去高阶项的系数，剩下f(n)，则时间复杂度为：
。
我们通常用的都是大O表示法，也就是这个算法执行时最差的结果。
如果指标不能分析出哪个算法更好的时候（比如算法复杂度相同），就需要根据实际代码运行时间来判断了。
选择排序
数组长度为 n ，每次从 i 到 n 找最小值放到 i 位置去。
[0,5,8,2,3,4]
[0] (访问6次，比较5次，交换0次)
[0,2] (访问5次，比较4次，交换1次)
[0,2,3] (访问4次，比较3次，交换2次)
[0,2,3,4] (访问3次，比较2次，交换2次)
[0,2,3,4,5] (访问2次，比较1次，交换1次)
[0,2,3,4,5,8] (访问1次，比较0次，交换0次)我们类推假如数组有 n 项，则进行选择排序的话：
- 访问总次数：n+(n-1)+(n-2)+...
- 比较次数：n-1+(n-2)+...
- 交换次数：常数次c
总的常数操作估算为 : 
，这么一个一元二次方程。
因为等差数列求和公式为：
，计算可得：
- 访问次数 =
- 比较次数=
- 交换次数 = c
总的常数操作次数 = 
，所以选择排序的时间复杂度计算为：
。
代码实现
public static void selectSort(int[] arr){
for(int i=0;iarr[j]){
int tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
}
}
} 冒泡排序
数组长度为 n ，每次从下标0处开始对相邻元素进行比较，大的数向右移，第一次循环最大的数移动到第下标为 n-1 处，第二次最大的数移动到下标为 n-2 处...循环 n-1次。
[0,5,8,2,3,4]
[0,5,2,3,4,8] (访问6次数，比较5次，交换3次)
[0,2,3,4,5,8] (访问5次，比较4次，交换3次)
[0,2,3,4,5,8] (访问4次，比较3次，交换0次)
[0,2,3,4,5,8] (访问3次，比较2次，交换0次)
[0,2,3,4,5,8] (访问2次，比较1次，交换0次)
[0,2,3,4,5,8] (访问1次，比较0次，交换0次)冒泡排序时间复杂度：。
代码实现
public static void maoPaoSort(int[] arr){
for(int i=0;iarr[j+1]){
int tmp = arr[j+1];
arr[j+1] = arr[j];
arr[j] = tmp;
}
}
}
} 异或运算（^）
核心：相同为0，不同为1
异或运算可以理解为无进位相加：
a: 100011
b: 010111
^ ------
= 110100性质
- 0^N=N（N代表任意数）
- N^N=0
- 交换律和结合律：a^b=b^a (a^b)^c=a^(b^c)
异或的使用
1、交换两个数的值
前提：两个值指向内存中不同的两块区域，比如交换数组arr中相同位置的两个数必然导致该位置的值变为0。
int a = 甲
int b = 乙
a = a^b a=甲^乙 b=乙
b = a^b a=甲^乙 b=甲^乙^乙=甲^0=甲
a = a^b a=甲^乙^甲=(甲^甲)^乙=0^乙=乙 b=甲
代码实现
//如果i和j为同一个值的话,会出错
public static void swap(int[] arr,int i,int j){
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}例题1
数组中一种数出现了奇数次，其它的数都出现了偶数次，怎么找到出现了奇数次的数。
要求：时间复杂度 = 
。
思路：使用一个变量0从头到尾对数组进行异或运算，将出现偶数次的数除去，剩下的就是只出现了奇数次的数。
int[] arr = {1,2,2,3,3,4,4};
int eor=0;
for (int n : arr) {
eor = eor ^ n; //1^2^2^3^3^4^4=1
}
System.out.println(eor);//1例题2
数组中两种数出现了奇数次，其它都出现了偶数次，怎么找到这两个出现了奇数次的数。
要求：时间复杂度 = 。
思路：
- 和例题1一样，我们假如同样利用一个变量 eor 去从头到尾对数组进行异或运算，这次的结果将是两个出现了奇数次的数的异或结果，我们假设为 eor = a^b 。
- 因为出现奇数次的数是两种数，所以一定有
，所以意味着此时 eor 对应的二进制数一定有一位等于 1（因为每一位全部等于0的话这个值就是0，但这里 ，所以 eor=a^b 绝不可能等于0）。 - 根据某一位来分类，我们知道eor=a^b，而eor的二进制中位上值为1说明a和b该位上的值是不同的，一个为0一个为1。我们假设eor的第 i 位为1，就是说 a 的第 i 位和 b 的第 i 位一定不一样，这个时候所有的数都被分为两类，第 i 位为1的和为0的，其中a和b肯定各占一类。
- 因为eor的二进制数中，可能不止一个位上的值为1，所以我们需要引进变量
(eor'=eor (~eor + 1))来取出eor中最右边的1（比如eor=10011011则对应eor'=00000001）。用去对数组中所有数进行 &运算，这样就把数组分为了两部分，&运算后为0的和为1的，出现偶数次的数自然会被放到一类。 - 分为两类后，我们使用0进行异或运算（因为0^任意数=任意数），这样就把偶数次的数除去了，一个类里就只剩下我们的a或者b。
- 怎么区分a和b的值？我们只需要用eor（a^b）去和上面的结果（a或者b的值）进行异或运算就可以得到另一个数了（因为 a^a^b=b,b^a^b=a）。
代码实现
int[] arr = {1,2,2,3,3,4,4,5};
int eor=0;
for (int a : arr) {
eor = eor^a;
}
//eor = a ^ b
//aor != 0
//eor 必然有一位是1
//eor这个数中,位上为1的地方a或b肯定有一个为1一个为0
//（因为eor=a^b,所以只有a和b位上不同才会使得eor某位上的值=1),所以我们下面使用最右边的1作为区分a和b的关键，这才是我们把a和b区分到两个类的关键
//a 01011100
//b 11000111
//eor 10011011 位上为1的部分说明必然有a或b该位一个为0一个为1
//~eor 01100100
//~eor+1 01100101
//eor&(~eor+1) 00000001
int rightOne = eor & (~eor + 1);//提取出eor最右边的 1
int onlyOne = 0; //eor'
for (int cur : arr) {
//因为rightOne=00000001，0&任意数=0，所以可以根据最后一位来将数组中所有数分为两类
if((cur & rightOne) == 0){
onlyOne ^= cur;//偶数个的数被异或运算抵消 只剩下a或者b
}
}
System.out.println(onlyOne +" "+(eor ^ onlyOne)); 我们可以看到，使用位运算我们只需要遍历1遍数组就可以实现例题1，遍历两遍数组就可以实现例题2。最重要的是复杂度仅为 ，除此之外，要知道位运算是要比算术运算快很多的！
插入排序
先做到下标0~0范围是有序的，再做到0~1范围是有序的，...最后做到0~n是有序的。类似于斗地主的时候，来一张牌就从左往右从大到小选择合适的位置插入这张牌。
[3,2,5,4,2,3,3]
[3] 0~0有序
[2,3] 0~1有序
[2,3,5] 0~2有序
[2,3,4,5] 0~3有序
[2,2,3,4,5] 0~4有序
[2,2,3,3,4,5] 0~5有序
[2,2,3,3,3,4,5] 0~6有序时间复杂度： 。（时间复杂度是按照该算法的最差的情况取的）。
- 当数组本来就有序时，插入排序的时间复杂度可以仅为：
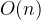。 - 当数组逆序时，时间复杂度最差为：
。
[1,2,3,4,5]
[1] 0~0 比较1次，交换0次
[1,2] 0~1 比较1次，交换0次
[1,2,3] 0~2 比较1次，交换0次
[1,2,3,4] 0~3 比较1次，交换0次
[1,2,3,4,5] 0~4 比较1次，交换0次
[5,4,3,2,1]
[5] 0~0 比较1次，交换0次
[4,5] 0~1 比较1次，交换1次
[3,4,5] 0~2 比较1次，交换2次
[2,3,4,5] 0~3 比较1次，交换3次
[1,2,3,4,5] 0~4 比较1次，交换4次代码实现
public static void insertSort(int[] arr){
// 0~0有序
// 0~i有序
for (int i = 0; i < arr.length; i++) {// 0~i做到有序
for (int j = i-1; j >= 0 && arr[j] > arr[j+1]; j--) {
swap(arr,j,j+1);
}
}
}二分法
定义
二分法用于查找某个值，查找时它一次砍一半，一次砍一半，直到找到为止，砍的次数就是二分法的时间复杂度。
时间复杂度：
，以2为底的时间复杂度在算法默认用
表示 ，如果是别的数(比如3，则用
来表示)。
比如下面我们从8个、16个数中找到我们目标的值的最坏次数结果：
8个 4个 2个 1个 最多砍3次
16个 8个 4个 2个 1个 最多砍4次leecode35.搜索插入位置
- 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
- 请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
思路：时间复杂度为 就是 ，也就是让我们使用二分法进行查找。
代码
class Solution {
public int searchInsert(int[] nums, int target) {
int left=0;
int right=nums.length-1;
if(targetnums[nums.length-1]){
return nums.length;
}
while(left <= right){
int mid = (left + right)/2;
if(nums[mid] > target){
right = mid-1;
}else if(nums[mid] < target){
left = mid+1;
}else{
return mid;
}
}
if(left>right){
return left;
}
return -1;
}
} leecode278.第一个错误版本
【题目链接】
大概意思就是说，一共有n个版本（从1到n），如果第 i 个版本出错了，那么后面的所有版本也就都错了，让你找到第一个出错的版本，也就是出错的源头。我们不需要关心出错的版本是哪个，只负责最快找到出错的版本就行，出错可以用isBadVersion(int version)来判断。用二分法最快了，因为测试集中有大到几十亿的测试值。
思路：用二分法发现一个错误版本后，这并不一定是第一个错的版本，所以需要继续向左继续查找，直到使得 left 和 right 指针错位，说明这个时候正好位于正确版本和错误版本的临界点。
时间复杂度： 。
/* The isBadVersion API is defined in the parent class VersionControl.
boolean isBadVersion(int version); */
public class Solution extends VersionControl {
public int firstBadVersion(int n) {
int left = 1;
int right = n;
if(n==1){
return 1;
}
while(left<=right){
//很神奇的一行代码,使用mid=(left+right)/2就会超时溢出
int mid = left+(right-left)/2;
if(isBadVersion(mid)){
right = mid-1;
}else{
left = mid+1;
}
}
if(left>right){
return left;
}
return -1;
}
}