leetcode：31. 下一个排列

题目来源

• leetcode：31. 下一个排列

题目描述

题目解析

分析

我们可以将该问题形式化地描述为：给定若干个数字，将其组合为一个整数。如何将这些数字重新排列，以得到下一个更大的整数。如 123 下一个更大的数为 132。如果没有更大的整数，则输出最小的整数。

如何得到这样的排列顺序呢？ 分析：

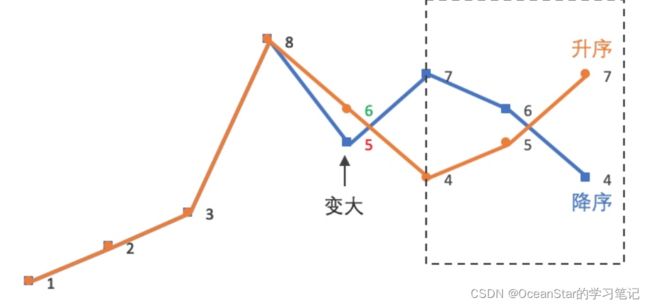
1. 我们希望下一个数比当前数大，就需要将后面的[大数]和前面的[小数]交换，这样就能得到一个更大的数。比如 123456，将 5 和 6 交换就能得到一个更大的数 123465。
2. 我们还需要下一个数增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“”的要求。为了满足这个要求，我们需要：
   • 尽可能靠右的低位进行交换，因此需要从后往前找
   • 将一个**尽可能小的[大数]**与前面的[小数]交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换

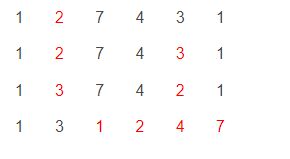
看个例子，假设样例为 [1,3,5,4,1]：

1. 从后往前找，找到第一个下降的位置，记为 k。注意k 以后的位置是降序的。 在样例中就是找到 3
2. 从 k 往后找，找到最小的比 k 要大的数。 找到 4
3. 将两者交换。注意此时 k 以后的位置仍然是降序的。得到[1, 4, 5, 3, 1]
4. 直接将 k 以后的部分翻转（变为升序）, 得到[1, 4, 1, 3, 5]

注意：如果在步骤 1 中找到头部还没找到，说明该序列已经是字典序最大的排列。按照题意，我们要将数组重新排列成最小的排列。

举个例子：

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int len = nums.size();

        // 从后往前找，找第一个降序
        for (int i = len - 1; i >= 0; --i) {
            if(i == 0){ // 全员升序
                std::reverse(nums.begin(), nums.end());
            }else{
                if(nums[i - 1] < nums[i]){  // 找到了
                    int k = nums[i - 1],  min = INT_MAX, min_j = i - 1;
                    // 从i开始找，找最小的比 k 要大的数(一定能找到)
                    for (int j = i; j < len; j++){
                        if(nums[j] > k){
                            min = std::min(min, nums[j]);
                            min_j = j;
                        }
                    }
                    // 交换
                    std::swap(nums[i - 1], nums[min_j]);
                    // 从i开始，将所有数逆转
                    std::reverse(nums.begin() + i, nums.end());
                    break;
                }
            }
        }
    }
};

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int len = nums.size();

        // 从后往前找，找第一个降序
        int i = len - 1;
        while (i - 1 >= 0 && nums[i - 1] >= nums[i]){
            --i;
        }

        if(i == 0){
            std::reverse(nums.begin(), nums.end());
        }else{
            // 从i开始找，找最小的比 k 要大的数(一定能找到)
            int k = nums[i - 1],  min = INT_MAX, min_j = i - 1;
            for (int j = i; j < len; j++){
                if(nums[j] > k){
                    min = std::min(min, nums[j]);
                    min_j = j;
                }
            }
            // 交换
            std::swap(nums[i - 1], nums[min_j]);
            // 从i开始，将所有数逆转
            std::reverse(nums.begin() + i, nums.end());
        }

    }
};

类似题目

题目	思路
leetcode：46. 给定(无重复)数组nums，生成所有可能的全排列Permutations
leetcode：47. 给定(可重复)数组nums，生成所有可能的(不重复)全排列Permutations II
leetcode：31. 给定(可重复)数组nums，生成下一个排列(字典序) Next Permutation	从后往前找，找第一个降序i；如果i=0，那么直接逆序；如果i不为0，那么从i往后找找最小的比 k 要大的数，交换num[min_j]与num[i]，最后从i开始，将所有数逆转
leetcode：60. 给定集合[1…n]，返回生成第k个序列(字典序) Permutation Sequence
leetcode：77. 给定集合[1…n]，所有可能的 k 个数的组合 Combinations	排列问题（46）每次通过used来排除在dfs中已经选择过的数字；而组合问题通过每次传入一个start参数，来排除start索引之前的数字
leetcode：266. 能不能生成回文全排列 Palindrome Permutation	奇数个的字符只能是0个或者1个，其余的必须是偶数个
leetcode：267. 能够生成的所有回文全排列 II Palindrome Permutation II	怎么确保生成的一定是回文串呢？