量化投资 现代投资组合理论（MPT）

量化投资 现代投资组合理论（MPT）

问题：构建投资组合，达到目标收益率的同时拥有最小的 risk exposure.

• 有 $J$ 个可交易证券，期望收益率为 $R=[R_1,\cdots ,R_j{]}^T$，无风险利率为 $R^f$ ；

• 令 $\mu \in {\mathbb{R}}^J$ 为期望收益率，$\Sigma$ 为期望收益率的协方差矩阵；

• 投资组合 $\theta =[{\theta }_1,\cdots ,{\theta }_J{]}^J$ ，满足 ${\theta }^{T}e=1$ ，${\theta }_i$ 代表投资于第 $j$ 个证券的资产比例；

• 投资组合 $\theta$ 的期望收益率为：$\mu [\theta ]=R^{\theta }=R^f+{\theta }^T(\mu -R^{f}e)$ ，标准差为 $\sigma [\theta ]=({\theta }^T\Sigma \theta {)}^{\frac{1}{2}}$ ；

• 不同投资组合之间的协方差为：$\sigma [\theta ,{\theta }^{\prime }]={\theta }^T\Sigma {\theta }^{\prime }$ ；

有效投资组合 Efficient Portfolio：投资组合 ${\theta }_0$ 在 ${\mu }_0$ 处是 mean-variance efficient，若 ${\theta }_0$ 的期望收益为 ${\mu }_0$ ，并且不存在其他达到同样期望收益率且拥有更小方差的投资组合。即：
$${\theta }_0\in \arg \min \{{\sigma }^2[\theta ]|\mu [\theta ]={\mu }_0\}$$
该问题可以写成最优化问题：
$${\theta }_0=\arg \min \{\frac{1}{2}{\theta }_0^T\Sigma {\theta }_0:{\theta }^T\mu ={\mu }_0\text{ and }{\theta }^{T}e=1\}$$
其中的 $\frac{1}{2}$ 是为了便于求导。构建 Lagrangian：
$$L=\frac{1}{2}{\theta }^T\Sigma \theta +{\lambda }_1({\theta }^T\mu -{\mu }_0)+{\lambda }_2({\theta }^{T}e-1)$$
得到 FOC 为：
$$\{\begin{array}{l}\Sigma \theta +{\lambda }_1\mu +{\lambda }_{2}e=0\\ {\theta }^T\mu ={\mu }_0\\ {\theta }^{T}e=1\end{array}$$
由第一个式子，我们可以得到：
$$\theta =-{\Sigma }^{-1}[\mu ,e]\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\end{array}\right]$$
由第二个式子，我们可以得到：
$$[\mu ,e{]}^T\theta =\left[\begin{array}{c}{\mu }_0\\ 1\end{array}\right]$$
两个式子联立得到：
$$-[\mu ,e{]}^T{\Sigma }^{-1}[\mu ,e]\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\end{array}\right]=\left[\begin{array}{c}{\mu }_0\\ 1\end{array}\right]$$
令 $A=[\mu ,e{]}^T{\Sigma }^{-1}[\mu ,e]$ （$A$ 是一个 $2\times 2$ 的方阵），则：
$$\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\end{array}\right]=-A^{-1}\left[\begin{array}{c}{\mu }_0\\ 1\end{array}\right]$$
再代回去，得到：
$$\theta ={\Sigma }^{-1}[\mu ,e]A^{-1}[{\mu }_0,1]$$
方差为：
$${\sigma }_0^2={\theta }^T\Sigma \theta =[{\mu }_0,1]A^{-1}[{\mu }_0,1{]}^T$$
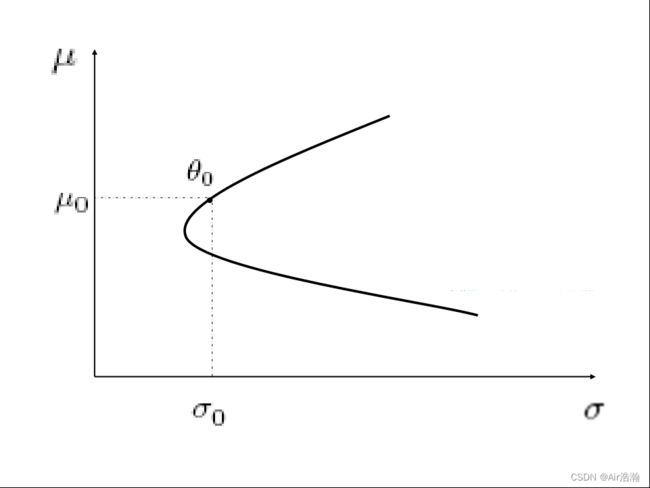
Markowitz’s MV Efficient Frontier：将上述解析解画出图像，可以得到：

最小方差投资组合：从图像中可以看出，投资组合中具有将 $\sigma$ 最小化的点，对应的最优化问题为：
$$\min {\theta }^T\Sigma \theta s.t.{\theta }^{T}e=1$$
Lagrangian 为：
$$L(\theta ;\lambda )={\theta }^T\Sigma \theta +\lambda (1-{\theta }^{T}e)$$
FOC 为：
$$\{\begin{array}{l}\frac{\partial L}{\partial \theta }=2\Sigma \theta -\lambda e=0\\ \frac{\partial L}{\partial \lambda }=1-\sum _{i=1}^n{\theta }_i=0\end{array}$$
解得：
$$\{\begin{array}{l}\underline{\theta }=\frac{{\Sigma }^{-1}e}{e^T{\Sigma }^{-1}e}\\ \lambda =\frac{2}{e^T{\Sigma }^{-1}e}\end{array}$$
即最小方差和最小方差对应的期望收益率为：
$$\begin{array}{rl}\underline{\mu }=& {\mu }^T\underline{\theta }=\frac{{\mu }^T{\Sigma }^{-1}e}{e^T{\Sigma }^{-1}e}\\ {\underline{\sigma }}^2=& {\underline{\theta }}^T\Sigma \underline{\theta }=\frac{e^T{\Sigma }^{-1T}e}{(e^T{\Sigma }^{-1}e{)}^2}\end{array}$$
最大夏普率投资组合：以纵坐标上一点 $(0,R^f)$ 向 frontier 做上切线，可以知道切点对应的投资组合是曲线上夏普率最大的投资组合（称为 tangency portfolio），对应最优化问题为：
$$\max \frac{{\theta }^T\mu -R_f}{({\theta }^T\Sigma \theta {)}^{\frac{1}{2}}}\text{s.t.}{\theta }^{T}e=1$$
Lagrangian 为：
$$L(\theta ;\lambda )=({\theta }^T\mu -R_f)({\theta }^T\Sigma \theta {)}^{-\frac{1}{2}}+\lambda (1-{\theta }^{T}e)$$
FOC 为：
$$\{\begin{array}{l}\frac{\partial L}{\partial \theta }=\mu ({\theta }^T\Sigma \theta {)}^{-\frac{1}{2}}-({\theta }^T\mu -R_f)({\theta }^T\Sigma \theta {)}^{-\frac{3}{2}}\Sigma \theta -\lambda e=0\\ \frac{\partial L}{\partial \lambda }=1-{\theta }^{T}e=0\end{array}$$
解得（这个没解出来。。。看的答案）：
$$\{\begin{array}{l}{\theta }_T=\frac{{\Sigma }^{-1}(\mu -R_{f}e)}{e^T{\Sigma }^{-1}(\mu -R_{f}e)}\\ \lambda =R_f({\theta }_T^T\Sigma {\theta }_T{)}^{-1}\end{array}$$