CMOS逻辑

---

一、反相器

  CMOS反相器即为非(NOT)门，是由一个pMOS管和nMOS管串联构成。下图为反相器的电路图(a)和符号图(b)：

  当输入A为0时，pMOS管导通，nMOS管关闭，输出Y接通VDD，Y被上拉至1；
  当输入A为1时，pMOS管关闭，nMOS管导通，输出Y接通GND，Y被下拉至0；

表达式为：
$$Y=\overline{A}$$

反相器真值表

A	Y
0	1
1	0

---

二、与非门（NAND）

  二输入与非门由两个输入条件，它是由两个在Y与GND之间串联的nMOS管和在Y与VDD之间并联的pMOS管构成。下图为与非门的电路图(a)和符号图(b)：

表达式为：
$$Y=\overline{A\cdot B}$$

与非门真值表

A	B	上拉网络(pMOS管)	下拉网络(nMOS管)	Y
0	0	关闭	导通	1
0	1	关闭	导通	1
1	0	关闭	导通	1
1	1	导通	关闭	0

  k输入的与非门是由k个串联的nMOS管和k个并联的pMOS管构成，例如下图三输入的与非门：

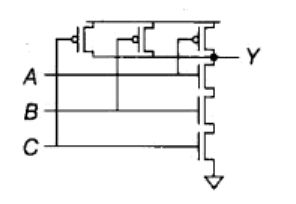
表达式为：
$$Y=\overline{A\cdot B\cdot C}$$

---

三、逻辑门

  上述所描述的反相器和与非门就是两种静态的CMOS逻辑门也称为互补CMOS门。一般一个静态的CMOS逻辑门就是由一个输出连接GND的nMOS下拉网络和一个输出连接VDD的pMOS上拉网络构成，必有一个导通一个关闭。下图为逻辑门的结构图：

CMOS逻辑门的输出状态

	上拉网络关闭	上拉网络导通
下拉网络关闭	Z	1
下拉网络导通	0	X

  Z状态：是在上拉和下拉网络都关闭的时候，就会形成高阻(Z)即浮空的状态。这个状态在多路开关、储存单元以及三态总线驱动器中很有意义。
  X状态：是在上拉和下拉网络都导通的时候，就会形成竞争电平(X)。此时两个网络间的竞争将产生一个不确定的输出电平并引起静态功耗，这通常不是我们所希望出现的。

---

四、或非门

  二输入或非门是由两个在Y与GND之间并联的nMOS管和在Y与VDD之间并串的pMOS管构成。下图为与非门的电路图(a)和符号图(b)：

表达式为：
$$Y=\overline{A+B}$$

或非门真值表

A	B	上拉网络(pMOS管)	下拉网络(nMOS管)	Y
0	0	导通	关闭	1
0	1	关闭	导通	0
1	0	关闭	导通	0
1	1	关闭	导通	0

---

五、复合门

  复合门是由通过串联和并联开关结构的组合来实现的。以单级逻辑完成复杂的逻辑功能。

表达式$Y=\overline{(A\cdot B)+(C\cdot D)}$的复合门为：

表达式$Y=\overline{(A+B+C)\cdot D)}$的复合门为：

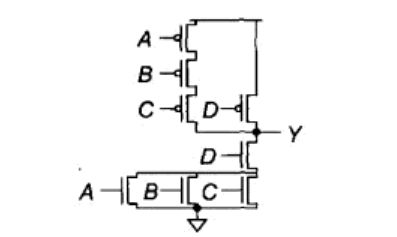
思路：
   当D为1并且A或B或C中任何一个为1时,nMOS下拉网络将使输出下拉为低电平，所以D和A、B及C的并联组合串联在一起。由于pMOS上拉网络是nMOS 下拉网络的“互补导通”，所以在pMOS上拉网络中D必须和A、B及C的串联组合相并联。

另类思路：
   nMOS管：或并与串
   pMOS管：或串与并

---

六、传输管和传输门

  nMOS管传送0时，是近似理想的称为“强0”，但是传送1时，却不理想，称为降级1或“弱1”；pMOS管则状态相反，“强1弱0”。

  当pMOS管和nMOS管单独用来作为一个非理想开关时，称为它是传输管。

  当一个pMOS管和一个nMOS管并联在一起时，无论是0还是1都能被这个开关以一种可以接受的方式传送出去，称它为传输门或传送门。

  目的： 在g=1，gb=0时，在a端输入0或1时，都可在b端输出强0或强1.

---

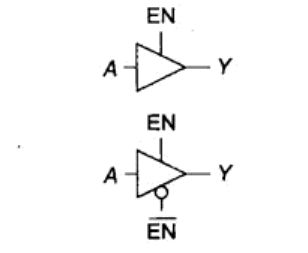
七、三态门

  外加一个使能信号，使输出呈现了三种状态：0、1、Z(悬空)。

下图就是三态缓存器的符号：

下图为三态门的真值表：

$EN/$ $\overline{EN}$	A	Y
0/1	0	Z
0/1	1	Z
1/0	0	0
1/0	1	1

三态反相器：

  当EN为0时(见图(b))，两个使能晶体管关断，使输出端浮空；当EN为1时(见图©)，两个使能晶体管导通。

---

八、多路开关

  多路开关即是根据选择信号从它的几个输入中选择其中一个作为输出。

  例如：二输入即2:1的多路开关，当选择信号为0时选择D0输入，而当选择信号为1时选择D1输入。
其逻辑函数为：
$$Y=\overline{S}\cdot D0+S\cdot D1$$
其电路图为：

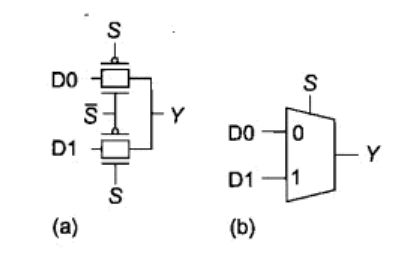
其真值表为：

$S/$ $\overline{S}$	D1	D0	Y
0/1	X	0	0
0/1	X	1	1
1/0	0	X	0
1/0	1	X	1

  可见，二输入的多路开关是由二个传输门构成。同时，二输入的多路开关亦可用二个三态反相器构成。

  较大的多路开关可以用多个二输人多路开关构成或直接把几个三态反相器组合在一起构成，但每个三态反相器需要有–个译码使能信号，这些使能信号应当同时翻转以防止竞争。

---

九、锁存器和触发器

  时序电路：它们的输出同时取决于当前和之前的输入。

  由一个二输入多路开关和两个反相器构成的D锁存器（电平灵敏锁存器）。电平灵敏锁存器因为输出状态取决于时钟信号的电平。

  当CLK=1时锁存器透明，因而D通过它到达Q(见图©)。当CLK下降至0时，锁存器将变为不透明。此时沿这对反相器建立起一条反馈路径(见图(d))，使当前的Q状态能无限期地保持下去。

---

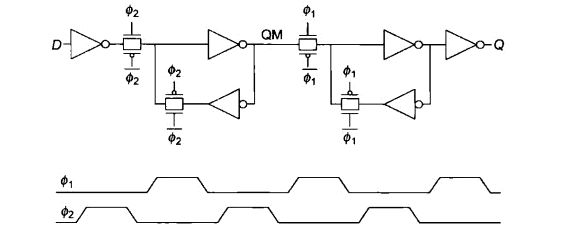
  将两个电平灵敏锁存器（一个负电平灵敏和另一个正电平灵敏）连在一起，就构成了下图的边缘触发器。第一级锁存器称为主锁存器，第二级称为从锁存器。

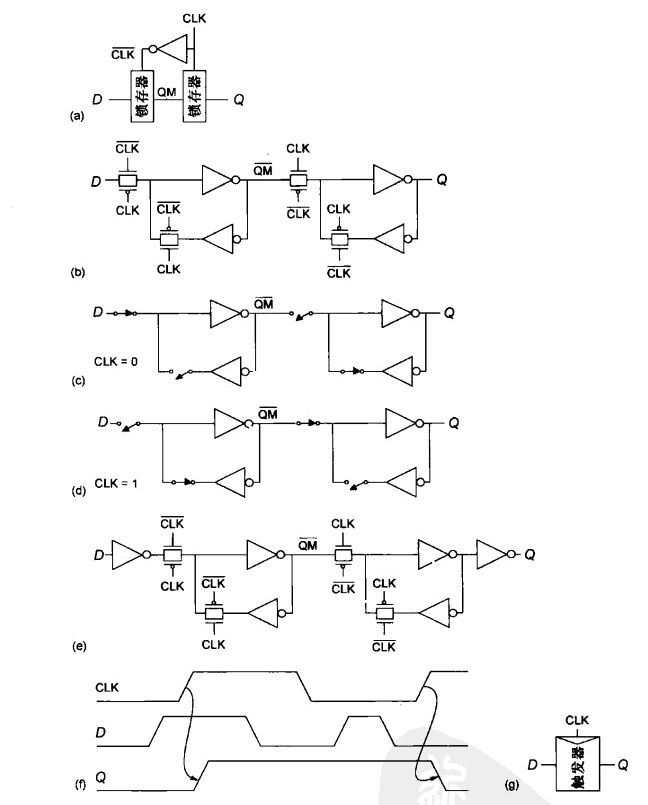
  当CLK为低时，负电平灵敏主锁存器的输出($\overline{QM}$)跟随输入D而变化，此时正电平灵敏的从锁存器保持它原来的值(见图©)。当时钟从0跳变到1时，主锁存器变为不透明并保持在时钟跳变时的D值，而从锁存器变为透明，将主锁存器所保存的值($\overline{QM}$)传送至从锁存器的输出(Q)。由于此时主锁存器已与输人D断开(见图( d))，因而输入D被阻止而不会影响输出。当时钟从1跳变至0时，从锁存器保持它的值而主锁存器开始再次采样输入数据。

  如果系统的时钟偏斜(clock skew)太大，即由于时钟到达时间的不同使一个触发器触发得早些而另一个触发器触发得晚些，那么触发器就有可能发生保持时间( hold-time)失效。为解决这一问题可以采用两相位不重叠时钟的时序控制来完全避免保持时间问题。

  下图为用两相不重叠时钟控制的触发器。只要两个相位在任何情况下都不重叠，那么无论何时至少有一个锁存器不透明，因而绝不会发生保持时间问题。