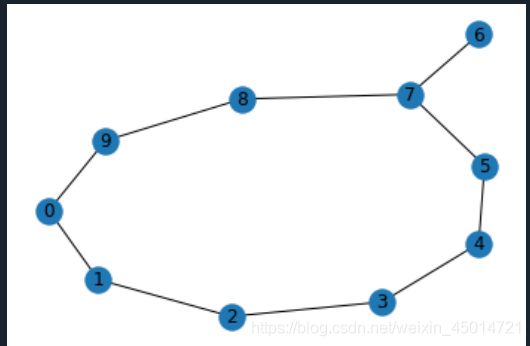
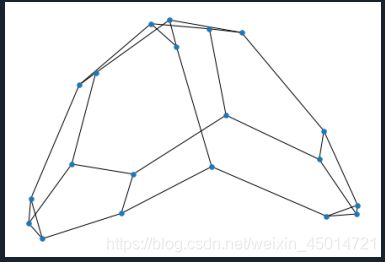
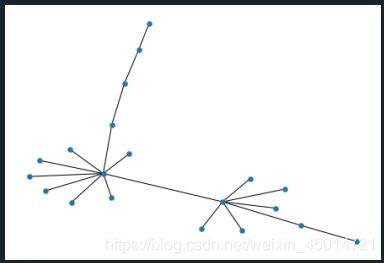
（3-2）networkx之用graph绘制简单图

1》graph的各种图形

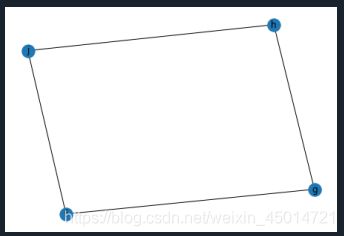
1.atlas（i）
这是一个编号好的网络图集，输入编号可以获得对应的图信息。编号从0到1252,节点从0个到8个。
（意思就是说atlas（i）每一个i对应一幅固定的图，这1252幅图都是编制好的）

import networkx as nx
graph = nx.graph_atlas(100)
nx.draw(graph,with_labels=True)#with_labels=True节点上标有数字

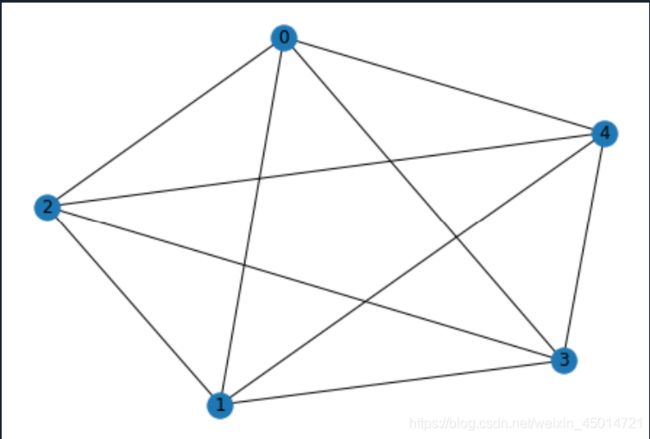
2.complete_graph(n)
返回节点数为n的完全图

import networkx as nx
graph = nx.complete_graph(5)
nx.draw(graph,with_labels=True)

3.circulant_graph(n, offsets)
返回n个节点的循环图，offsets是除了和相邻节点连接之外的连接节点的编号
eg: graph = nx.circulant_graph(10,range(3))

import networkx as nx
graph = nx.circulant_graph(10,range(3))
nx.draw(graph,with_labels=True)

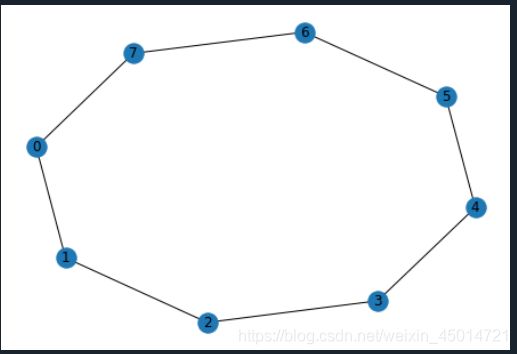
4.cycle_graph(n)
返回节点数为n的顺次连接的环

import networkx as nx
graph = nx.cycle_graph(8)
nx.draw(graph,with_labels=True)

5.empty_graph（n）
返回n个节点0条边的图

import networkx as nx
graph = nx.empty_graph(8)
nx.draw(graph,with_labels=True)

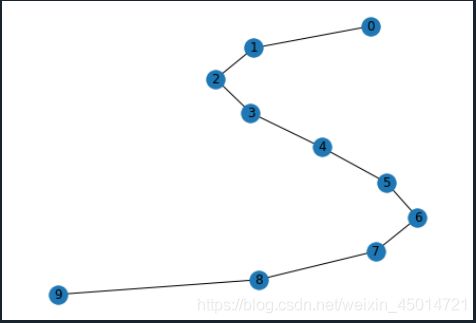
6.path_graph(n)
返回节点数为n的一条线图

import networkx as nx
graph = nx.path_graph(8)
nx.draw(graph,with_labels=True)

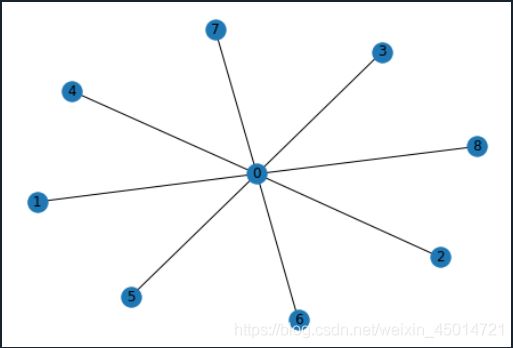
7.star_graph(n)
返回一个中心，n个叶子的星图

import networkx as nx
graph = nx.star_graph(8)
nx.draw(graph,with_labels=True)

2》一次性绘制多张graph图

声明,文中重复使用了以下代码块 ,现在统一注释在这里:

plt.subplot(221)  #生成2*2的组图,并且当前子图在2*2矩阵的第一个位置.第二个位置是222
plt.title('complete_graph') #子图的标题
nx.draw(G, with_labels=True, font_weight='bold') #将graph画出来
plt.axis('on') #需要坐标轴,以便框住graph
plt.xticks([]) #横坐标不需要刻度
plt.yticks([]) #纵坐标不需要刻度

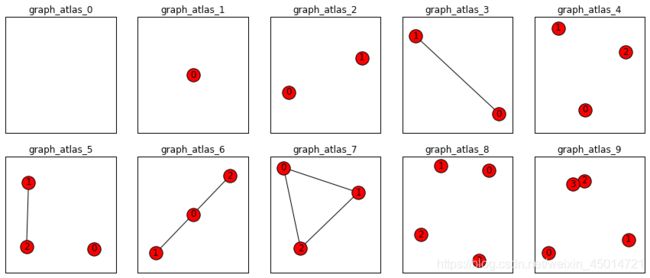
2.1小图图集的生成器
#graph_atlas(i)的图已经被定义,只需要按标号取出来就可以,下面将前10个取出来

import matplotlib.pyplot as plt
import networkx as nx

plt.subplots(2,5,figsize=(15,6)) 
#把绘图区域分成2排5列,figsize是限制整个绘图区域的长和宽的

for ind in range(10):
    plt.subplot(2,5,ind+1)
    
    G=nx.graph_atlas(ind)#得到相应的图
    nx.draw(G,with_labels=True)#with_labels=True节点上标有数字
    
    #下面是设置图片
    plt.axis('on')
    plt.title('graph_atlas_%s'%ind)
    plt.xticks([])
    plt.yticks([])
plt.show()

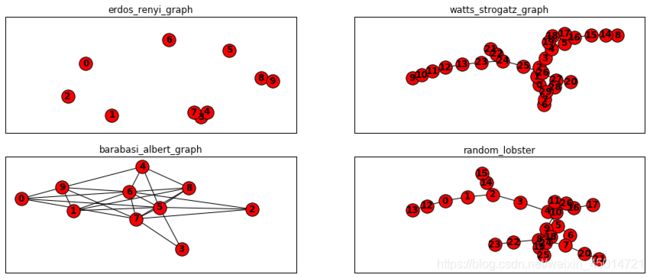
2.2使用随机graph生成器

import matplotlib.pyplot as plt
import networkx as nx

plt.subplots(2,2,figsize=(15,6))

plt.subplot(221)
er = nx.erdos_renyi_graph(10, 0.15)
nx.draw(er, with_labels=True, font_weight='bold')
plt.title('erdos_renyi_graph')
plt.axis('on')
plt.xticks([])
plt.yticks([])

plt.subplot(222)
ws = nx.watts_strogatz_graph(30, 3, 0.1)
nx.draw(ws, with_labels=True, font_weight='bold')
plt.title('watts_strogatz_graph')
plt.axis('on')
plt.xticks([])
plt.yticks([])

plt.subplot(223)
ba = nx.barabasi_albert_graph(10, 5)
nx.draw(ba, with_labels=True, font_weight='bold')
plt.title('barabasi_albert_graph')
plt.axis('on')
plt.xticks([])
plt.yticks([])

plt.subplot(224)
red = nx.random_lobster(10, 0.9, 0.9)
nx.draw(red, with_labels=True, font_weight='bold')
plt.title('random_lobster')
plt.axis('on')
plt.xticks([])
plt.yticks([])

plt.show()

3》极其重要的图

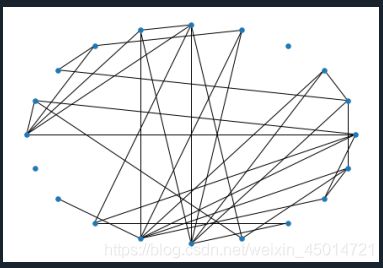
1.ER随机网络

ER随机图是早期研究得比较多的一类“复杂”网络，这个模型的基本思想是以概率p连接N个节点中的每一对节点。在NetworkX中，可以用random_graphs.erdos_renyi_graph(n,p)方法生成一个含有n个节点、以概率p连接的ER随机图：

import networkx as nx
import matplotlib.pyplot as plt
ER = nx.random_graphs.erdos_renyi_graph(20,0.2)  #生成包含20个节点、以概率0.2连接的随机图
pos = nx.shell_layout(ER)          #定义一个布局，此处采用了shell布局方式
nx.draw(ER,pos,with_labels=False,node_size = 30) 
plt.show()

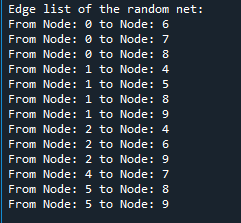
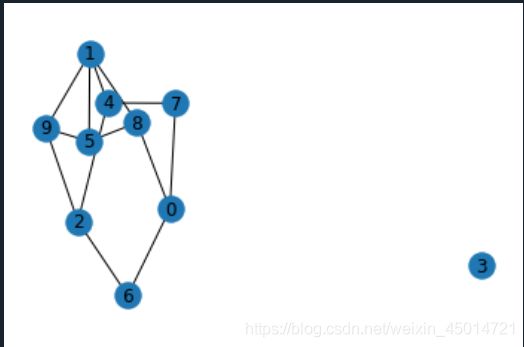
（2）

import matplotlib.pyplot as plt
import networkx as nx

random_net=nx.erdos_renyi_graph(10, 0.2)# 随机生成10个节点，节点间的连接概率都是0.2
print('Edge list of the random net:')
for n1,n2 in random_net.edges():
    print('From Node:',n1,'to Node:',n2)
nx.draw_networkx(random_net)#nx.draw_networkx(G)节点自带标签，nx.draw(G)节点不带标签
plt.axis('off')
plt.show()

（3）给网络加一条边

2.小世界网络

import matplotlib.pyplot as plt
import networkx as nx

#生成一个含有n个节点、每个节点有k个邻居、以概率p随机化重连边的WS小世界网络
sw_net=nx.watts_strogatz_graph(10,3, 0.4)
print('Edge list of the random net:')
for n1,n2 in sw_net.edges():
    print('From Node:',n1,'to Node:',n2)
nx.draw_networkx(sw_net)#nx.draw_networkx(G)节点自带标签，nx.draw(G)节点不带标签
plt.axis('off')
plt.show()

import networkx as nx
import matplotlib.pyplot as plt
WS = nx.random_graphs.watts_strogatz_graph(20,4,0.3)
#生成包含20个节点、每个节点4个近邻、随机化重连概率为0.3的小世界网络
pos = nx.circular_layout(WS) 
#定义一个布局，此处采用了circular布局方式，没有这个布局更像一张乱网而不是一个圈
nx.draw(WS,pos,with_labels=False,node_size = 30)  #绘制图形
plt.show()

3.绘制规则网络

规则图差不多是最没有复杂性的一类图了，在NetworkX中，用 random_graphs.random_regular_graph(d, n)方法可以生成一个含有n个节点，每个节点有d个邻居节点的规则图。下面是一段示例代码，生成了包含20个节点、每个节点有3个邻居的规则图：

import networkx as nx
import matplotlib.pyplot as plt
RG = nx.random_graphs.random_regular_graph(3,20)  #生成包含20个节点、每个节点有3个邻居的规则图RG
pos = nx.spectral_layout(RG)          #定义一个布局，此处采用了spectral布局方式
nx.draw(RG,pos,with_labels=False,node_size = 30)  #绘制规则图的图形，with_labels决定节点是非带标签（编号），node_size是节点的直径
plt.show()  #显示图形

4.BA无标度网络

在NetworkX中，可以用random_graphs.barabasi_albert_graph(n, m)方法生成一个含有n个节点、每次加入m条边的BA无标度网络，下面是一个例子：

import networkx as nx
import matplotlib.pyplot as plt
BA= nx.random_graphs.barabasi_albert_graph(20,1)  #生成n=20、m=1的BA无标度网络
pos = nx.spring_layout(BA)          #定义一个布局，此处采用了spring布局方式
nx.draw(BA,pos,with_labels=False,node_size = 30)  #绘制图形
plt.show()

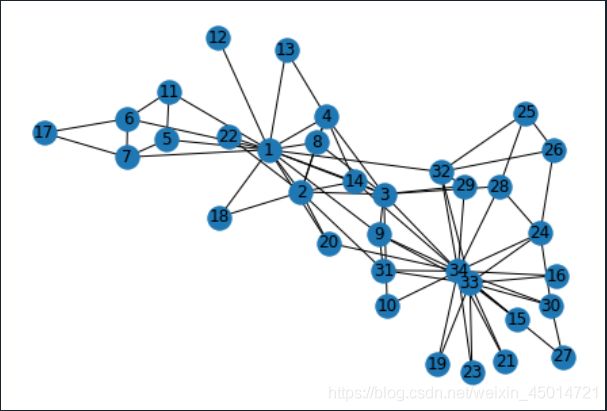
5.空手道俱乐部

import networkx as nx
g=nx.karate_club_graph()
nx.draw(g)

6.其他重要的图

add_star(G_to_add_to, nodes_for_star, **attr)：在图形G_to_add_to上添加一个星形。

add_path(G_to_add_to, nodes_for_path, **attr)：在图G_to_add_to中添加一条路径。

add_cycle(G_to_add_to, nodes_for_cycle, **attr)：向图形G_to_add_to添加一个循环。

import networkx as nx
import matplotlib.pyplot as plt
 
G = nx.Graph()                 #建立一个空的无向图G
nx.add_cycle(G,['f','g','h','j'])     #加环
nx.draw(G, with_labels=True)
plt.show()

import networkx as nx
import matplotlib.pyplot as plt
H = nx.path_graph(10)    #返回由10个节点挨个连接的无向图，所以有9条边
nx.draw(H, with_labels=True)
plt.show()

import networkx as nx
import matplotlib.pyplot as plt
 
G = nx.Graph() 
H = nx.path_graph(10)    #返回由10个节点挨个连接的无向图，所以有9条边
G.add_nodes_from(H)   #或G.add_node(H)

nx.draw(G, with_labels=True)
plt.show()

5》创建自定义的图像

（不套用公式创建图）
1.无向图

import networkx as nx
nodes=['a','b','c',0,1,2,3,4,5]
edges=[('a','b'),('b','c'),('c','a'),(0,1),(0,5),(1,2),(2,4),(1,4)]

G=nx.Graph()

G.add_nodes_from(nodes)
G.add_edges_from(edges)

nx.draw(G,with_labels=True)

2.有向图

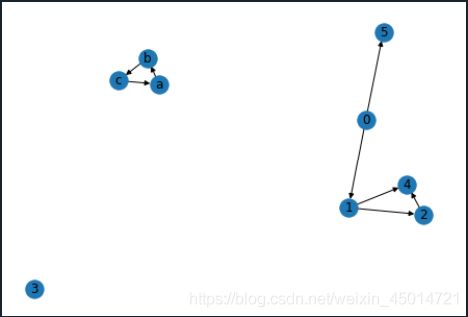
import networkx as nx
nodes=['a','b','c',0,1,2,3,4,5]
edges=[('a','b'),('b','c'),('c','a'),(0,1),(0,5),(1,2),(2,4),(1,4)]

G=nx.DiGraph()

G.add_nodes_from(nodes)
G.add_edges_from(edges)

nx.draw(G,with_labels=True)

③利用外部文件创建图
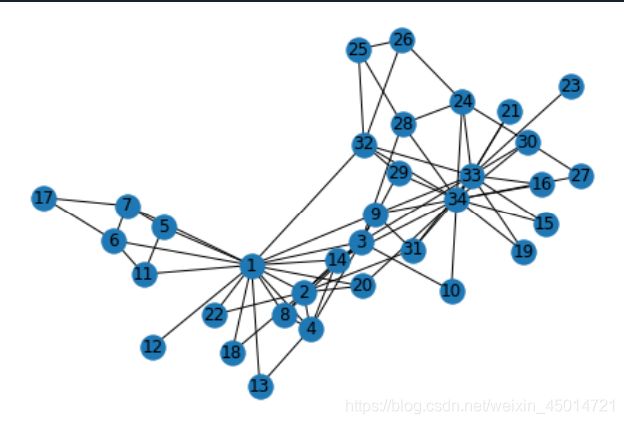
1.如何从矩阵中读取边

已知一个网络矩阵如下，请输出这个网络的边，并将网络绘制出来

import networkx as nx
G = nx.Graph()#创建一个空的网络
with open( 'Karate_club.txt', 'r' )as file:
    lines = file. readlines( )
for i in range(len(lines)):
    lines[i] = lines[i].strip('\n').split(' ')
#lines[i].strip('\n')得到了[0 1 1 1...]
#lines[i].strip('\n').split(' ')得到了['0', '1', '1', '1'...,'0','']
    for j in range(len(lines[i])):
        if lines[i][j] == '1':
            G.add_edge(i + 1, j + 1)
nx.draw(G,with_labels=True)
print(list(G.edges))

已知一个网络连边如下，请将网络绘制出来

import networkx as nx
G = nx.Graph()
with open('karate_edges.txt', 'r' )as file:
    for line in file:
        a,b=line.strip('\n').split('\t')#\t 跳格,一个tap键的大小（下面有\t的解释）
        #也可以是a,b=line.strip('\n').split('	')
        G.add_edge(a,b)
nx.draw(G,with_labels=True)
print(list(G.edges))

\t是什么

#\t就是一个tap键
print("123")
print("\t123")
print("123\t456\t789")
print("\n123\n456\n789")
print("自然数：\n\t123\n\t456\n\t789")
print("\t\n123\t\n456\t\n789")