过控Matlab-串级控制系统的参数整定(二)

太原理工大学过程控制实验之串级控制系统的参数整定

实验内容

构成以锅炉温度为主变量，锅炉夹套温度为副变量的串级控制系统，假设主、副对象传递函数分别为

1.根据动态特性参数法对简单控制系统的控制器参数整定

1)建立被控系统的Simulink结构图，或利用程序建模。
根据系统单位阶跃响应，采用作图法或计算法建立原系统的近似模型

求得系统的增益 K、时间常数 T 和纯迟延时间τ。
2)Z-N工程整定方法

根据Z-N工程整定方法，可得
①P控制时：Kc=1/δ=T/(τK);
②PI控制时：Kc=1/δ=T/(1.1τK)；Ti=3.3τ；
③PID控制时：Kc=1/δ=T/(0.85τK)；
Ti=2τ；Td=0.5τ；Z

利用系统的Simulink方框图，将仿真时间设置为 200，设置相应的控制器参数后，启动仿真，便可在示波器中看到系统在P、PI和PID 控制时的单位阶跃响应曲线。

3)C-C工程整定方法
根据C-C工程整定方法的计算公式，
①P控制时：Kc=(T/τ+0.333)/K；
②PI控制时：Kc=(0.9T/τ+0.082)/K；
Ti=(3.33τ/T+0.3*(τ/T)^2)/(1+2.2τ/T)T
③PID控制时：Kc=(1.35T/τ+0.27)/K；
Ti=(2.5τ/T+0.5*(τ/T)^2)/(1+0.6τ/T)T
Td=(0.37τ/T)/(1+0.2τ/T)*T；

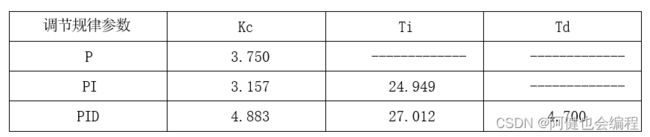保存系统在P、PI和PID控制时的单位阶跃响应曲线。
记录单闭环控制系统单位阶跃响应的性能指标于表2.1。

2.根据稳定边界方法对简单控制系统的控制器参数整定利用稳定边界法，分别计算系统采用P、PI、PID调节规律时的PID控制器参数，并保存

整定后系统的单位阶跃响应曲线，记录单闭环控制系统单位阶跃响应的性能指标于表2.1。
(1) 建立如图3所示的 Simulink 系统仿真框图。
(2) 首先在 MATLAB 工作窗口中，利用以下命令将图 2.2 中PID 控制器的积分时间设置为无穷大、微分时间设置为零、比例增益 Kc 设置较小的值。然后在图 2.2 中，将仿真时间设置为 200，启动仿真，便可在示波器中看到系统的单位阶跃响应曲线。
>>Ti=inf;Td=0;Kc=0.1
(3)逐渐增大比例系数 Kc，直到系统出现如图10所示的等幅振荡，即所谓临界振荡过
程。此时的比例系数被称为临界比例系数Kcr，两个波峰间的时间被称为临界振荡周期Tcr。
由上可知，临界比例带δcr =1/Kcr；临界振荡周期Tcr。

得到 Kc=10.4, Tcr=40
(4)利用δcr和Tcr值，根据稳定边界法相应的计算公式，求控制器各整定参数 Kc、Ti和Td 的数值。

①P控制时：Kc =1/(2δcr )=Kcr/2
②PI控制时：Kc =1/(2.2δcr )=Kcr/2.2 ；
Ti=0.85Tcr
③PID控制时：Kc =1/(1.67δcr )=Kc /1.67 ；
Ti =0.50Tcr ；Td =0.125*Tcr；

3.利用Simulink对简单控制系统PID控制器参数自整定

(1) 利用NCD Outport 模块（适用于 MATLAB6.5）或 Signal Constraint 模块（适用于MATLAB7.5），建立如图14所示 PID 控制系统Simulink参数优化模型。
(2)在系统模型窗口中，首先打开阶跃信号（Step）模块的参数对话框，并将初始时间改为0；然后执行Simulation parameters命令，将仿真的停止时间设置为100，其余参数采用默认值。
(3) 在MATLAB 窗口中利用以下命令对PID 控制器的初始值进行任意设置 ，
如 >>Kc=2.5;Ti=26;Td=13;
或者>>Kc=1;Ti=1;Td=1；
（4）根据系统给定的时域性能指标设置阶跃响应特性参数。
在系统模型窗口中，用鼠标双击NCD Outport 模块，即打开一个 NCD Outport 模块的时域性能约束窗口，如图15所示。

在 NCD Outport 模块的时域性能约束窗口中，执行 Options Step response 命令，打开设置阶跃响应特性约束参数的设置窗口。在该窗口中，设置阶跃响应曲线的调整时间(SettlingTime)为 25、上升时间(Rise Time)为15、超调量(Percent over shoot)为 12 和阶跃响应的优化终止时间（Final time）为 100，其余参数采用默认值。

（5）设置优化参数
在本例中为进行 PID 控制器的优化设计，将PID 控制器的参数 Kc、Ti 和 Td 作为 NCD Outport 模块的优化参数，故首先利用 Optimization Parameters 命令，打开设置优化参数（Optimization Parameters）的窗口。然后在该窗口中的优化变量名称（Tunable Varables）对话框中填写：Kc,Ti,Td（各变量间用西文逗号或空格分开），其余参数采用默认值，如图 2.6 所示。最后单击该窗口中的【Done】按钮接收以上数据。

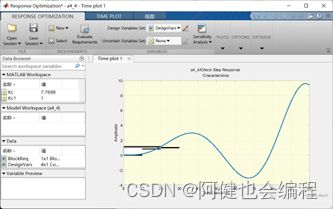
(7)优化结束后，再次启动仿真，在示波器中便可得到如图17所示的单位阶跃响应曲线

该曲线应该就是优化结束后的最优曲线。由此可见，PID控制器参数进行优化后，系统的动态性能指标完全满足设计要求。在MATLAB窗口中利用以下命令，便可得到PID控制器的优化参数，如 Kc=10.3813; Ti=81.6846; Td=6.9227。

4.利用MATLAB/Simulink 对串级控制系统进行参数整定

（1）设定控制系统所用主、副控制器的传递函数分别为：

(2) 利用NCD Outport模块，建立如图所示的串级控制系统的 Simulink 结构图。


整定主、副控制器的参数，并绘制整定后系统的单位阶跃响应曲线，记录串级控制系统单位阶跃响应的性能指标。

5.利用MATLAB/Simulink分析串级控制系统的抗干扰能力

对于串级控制系统，对于进入副回路的扰动，串级控制系统具有很强的抗干扰能力。并与单闭环控制系统对比。

如果将同样的扰动项加在主回路中，对比串级控制系统的抗干扰能力和单闭环控制系统的抗干扰能力。

6. 双容水箱液位串级控制系统实验

本实验以水箱1的液位为副调节器调节对象，水箱2的液位为主调节器调节对象，构成水箱液位串级控制系统，系统框图如图29所示。
启动 ForceControl 运行系统，建立“串级双容水箱液位控制”工程文件，如图30所示。连通阀 CV1 的开度为 100%，出水阀 CV2 至某一开度。主、副调节器置手动，采用手动操作使液位达到某一平衡状态。采用逐步逼近法进行主、副调节器参数整定。在主对象水箱 2 上施加扰动信号，观察液位响应曲线。在副对象水箱 1 上施加扰动信号，观察液位响应曲线。

思考题

1. 对比 Z-N 整定和 C-C 整定的控制器的控制效果。
由所得曲线知，Z-N 整定和 C-C 整定的P控制器的效果都较好，两三次振荡后就趋于稳定了，C-C整定的PI控制器的输出效果不佳，有频繁的振荡，两者整定的PID控制器都是一次振荡后就趋于稳定了，效果都十分好。

2. 比较等效简单控制系统和串级控制系统的抗干扰能力，并分析对一次和二次干扰的克服能力。
等效简单控制系统和串级控制系统的对一次干扰的抗干扰能力差不多，但串级控制系统对二次干扰的抗干扰能力比等效简单控制系统强很多。