第十二届蓝桥杯省赛Python大学组复盘

目录

一、前言

二、试题A：卡片（填空题）

三、试题B：直线（填空题）

四、试题C：货物摆放（填空题）

五、试题D：路径（填空题）

1、floyd变形

2、dijkstra

六、试题E：回路计数（填空题）

七、试题F：时间显示

八、试题G：杨辉三角形

九、试题H：左孩子右兄弟

十、试题I：异或数列

十一、试题J：括号序列

---

一、前言

这个月大概从10号开始，由于打软件精英挑战赛的缘故一直到27号都停下没怎么敲过题，前后大概半个月的时间没有管蓝桥杯比赛的事情，这是非常危险的，这周进行了一次赛题模拟及复盘，内容如下所示。

二、试题A：卡片（填空题）

题目链接：用户登录

这道题还是比较简单的，将数字转变成字符用函数count统计某个数字的个数，轻松搞定秒杀。

当然，还有另外的方法，打表尝试，主要用与查看一定范围内的数字1的个数，进而逐渐扩大结果范围。

#card={0:2021,1:2021,2:2021,3:2021,4:2021,5:2021,6:2021,7:2021,8:2021,9:2021}
ans=0
for i in range(1,5000):  #5000这个右边界肯定大于答案，因为是调试出来的，测试发现右边界是三千多
    c=str(i)
    ans+=c.count('1')
    if ans>2021:
        print(i-1)
        break
#print(ans)

三、试题B：直线（填空题）

题目链接：用户登录

这道题其实不怎么难，但是在计算截距 b 的这个细节上有坑，具体描述见代码。

s=set()
p=[]
n=21  #横坐标有n个数
m=20  #纵坐标有m个数
for i in range(0,n):
    for j in range(0,m):
        p.append((i,j))
from itertools import *
ans=0
for a in combinations(p,2):
    # print(a)
    x1,y1,x2,y2=a[0][0],a[0][1],a[1][0],a[1][1]
    if x2==x1 or y2==y1:
        continue
    #print(x1,y1,x2,y2)
    #k=round((y2-y1)/(x2-x1),8)          #没round保留位数则输出41255也是错的
    k=(y2-y1)/(x2-x1) 
    # print(k)
    #b1=y1-k*x1                 #这样计算结果错误！！！
    b=(x2*y1-x1*y2)/(x2-x1)        #用原始的两个点计算，不要用 k 计算，这样计算结果正确！！！
    #print(b,b1)                #通过输出发现 b1 的位数较少，猜测有可能是当 k 是除不尽的时候，利用 k 算的截距 b 就会发生一定的截断
    if (k,b) not in s:
        s.add((k,b))
        ans+=1
print(ans+m+n)      

这提示了我：用原本的数据计算目标变量，不要用中间产生的数据去计算！

四、试题C：货物摆放（填空题）

题目链接：用户登录

这道题啊，机灵一点，找这么大的一个数的三个因子，我实在是没有什么好的点子，唉。

但是，可以打表呀！用sqrt优化打表时间，n是16位数，sqrt(n)最多9位数吧，还是能遍历完的。

n=2021041820210418
#自己先打表
lst=[1, 2, 3, 6, 9, 17, 18, 27, 34, 51, 54, 102, 131, 153, 262, 306, 393, 459, 786, 918, 1179, 2227, 2358, 2857, 3537, 4454, 
     5714, 6681, 7074, 8571, 13362, 17142, 20043, 25713, 40086, 48569, 51426, 60129, 77139, 97138, 120258, 145707, 154278, 
     291414, 374267, 437121, 748534, 874242, 1122801, 1311363, 2245602, 2622726, 3368403, 5882353, 6362539, 6736806, 10105209, 
     11764706, 12725078, 17647059, 19087617, 20210418, 35294118, 38175234, 52941177, 57262851, 100000001, 105882354, 114525702, 
     158823531, 171788553, 200000002, 300000003, 317647062, 343577106, 600000006, 770588243, 900000009, 1541176486, 1800000018, 
     2311764729, 2700000027, 4623529458, 5400000054, 6935294187, 13100000131, 13870588374, 16805882521, 20805882561, 26200000262,
       33611765042, 39300000393, 41611765122, 50417647563, 78600000786, 100835295126, 117900001179, 151252942689, 235800002358, 
       285700002857, 302505885378, 353700003537, 453758828067, 571400005714, 707400007074, 857100008571, 907517656134, 
       1714200017142, 2201570610251, 2571300025713, 4403141220502, 5142600051426, 6604711830753, 7713900077139, 13209423661506, 
       15427800154278, 19814135492259, 37426700374267, 39628270984518, 59442406476777, 74853400748534, 112280101122801, 
       118884812953554, 224560202245602, 336840303368403, 673680606736806, 1010520910105209, 2021041820210418]
cnt=0
# length=len(lst)
# print(length)
for i in range(128):
    for j in range(128):
        for k in range(128):
            if n==lst[i]*lst[j]*lst[k]:
                cnt+=1
print(cnt)  #2430


# for i in range(2,int(n**0.5)+1):
#     if n%i==0:
#         lst.append(i)
#         lst.append(n//i)
#         cnt+=2
# lst.sort()
# print(lst)
# print(cnt)

这提示了我：一定一定要学会打表大法！解题不要死脑筋盯死在算法。打表真的香！

五、试题D：路径（填空题）

题目链接：用户登录

题目都意图很明显了吧，就是求最短路径，方法有很多种，floyd、dijkstra、bellman-ford、spfa都行，算法就不说了，我需要注意一些题目的描述或细节，题目构建的是有向图还是无向图，边权值又应该怎么赋值，这些构图的元素直接会导致结果是否正确。

1、floyd变形

from math import *
#mp=[i for i in range(2022)]
dp=[[1110000000]*2050 for i in range(2050)]

def floyd():
    for k in range(1,2022):
        for i in range(1,2):
            for j in range(1,2022):
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])

for i in range(1,2022):
    for j in range(i+1,i+22):
        w=i*j//gcd(i,j)
        dp[i][j]=w
        dp[j][i]=w

floyd()
print(dp[1][2021])

2、dijkstra

from math import *
from heapq import *
mp=[[] for _ in range(2025)]
dis=[999999999999999999999]*2025

def dij(s):
    dis[s]=0        #没了这个初始化，后果很严重
    A=[0]*2025
    B=[]
    heappush(B,(dis[s],s))
    A[s]=1
    while B:
        t=heappop(B)[1]
        A[t]=1
        for w,v in mp[t]:
            if A[v]:
                continue
            if dis[t]+w

六、试题E：回路计数（填空题）

题目链接：用户登录

这道题我一开始是解不出来的，看了题解我才幡然醒悟，这题要用状态压缩dp。

解释都在代码里了。

# dfs直接跑不出来，直接死
# 分析：状压dp。由于教学楼的个数很少,我们考虑用一个二进制位数等于21的数来表示教学楼的访问状态。
# 对该二进制数,如果它的第i位(二进制下)的值为1,则表示当前状态下第i栋教学楼已经访问过一次了;
# 若它的第i位(二进制下)的值为0,则表示当前状态下第i栋教学楼还未访问。于是可以定义dp[i][j]表示当前的状态为i,
# 最后走到的教学楼为j的方案数。

# 那么转移方程为: dp[i+(1<>k&1)=0) 且 j, k 之间存在路径。
# 最后答案为Σ(i从0到n) dp[(1 << 21) - 1][i] = 881012367360，时间复杂度为 O(21^2×2^21)。
from math import gcd
n = 21
m = 1 << n
dp = [[0 for j in range(n)] for i in range(m)]        #dp[i][j]对于状态i，i的二进制表示中为1的位置 表示走过了教学楼j
load = [[False for j in range(n)] for i in range(n)]  #存储i, j之间是否有路
for i in range(1, n + 1):
    for j in range(1, n + 1):
        if gcd(i, j) == 1:
            load[i - 1][j - 1] = True

dp[1][0] = 1
for i in range(1, m):           #枚举每一种状态
    for j in range(n):
        if i >> j & 1:          #判断状态i是否包含第j栋教学楼
            for k in range(n):  #枚举所有可能从教学楼k走到教学楼j的情况
                if i - (1 << j) >> k & 1 and load[k][j]:  #判断状态i除去j后是否包含k
                    dp[i][j] += dp[i - (1 << j)][k]

print(sum(dp[m - 1]) - dp[m - 1][0])    #输出结果：881012367360

若是这个代码不好理解，请看下面的C++。

#include
using namespace std;
typedef long long ll;

ll dp[1<<22][22];		//dp[i][j]表示当前状态为i，最后走到教学楼j的方案数
int g[22][22];			//邻接矩阵

int main() {
	int n=1<<21;      //状态数 (包括全为0，即000...00，这个状态，但该状态没有意义)
	
	for(int i=1;i<=21;i++)  	//构图 
	{
		for(int j=1;j<=21;j++)
		{
			if(__gcd(i,j)==1)
				g[i-1][j-1]=g[j-1][i-1]=1;   //顶点序号减1（在dp时，表示状态的整数的二进制形式，最低位为第0位） 
		}
	} 
	
	dp[1][0]=1;
	//n-1是全为1的状态，即21栋教学楼都走过了 
	for(int i=1;i>j&1))   //状态i里没有包含教学楼 j，跳过
				continue;
			for(int k=0;k<21;k++)    //考察从教学楼 j 到教学楼 k 
			{
				if(!g[j][k]||(i>>k&1))  //没路 或者 之前已经走过k了，则忽略 
					continue;
				dp[i+(1<

基于C++代码仿写的Python代码另解，如下。

# 跑出结果需要86s，这题是我在比赛中打开dev用C++写填空题也是很有必要的，C++跑出来需要2.7s
from math import *

n=1<<21                         #一开始这里我写成1<<22！我是真不看题啊！
dp=[[0]*22 for _ in range(n)]
g=[[0]*22 for _ in range(22)]

for i in range(1,22):
    for j in range(1,22):
        if gcd(i,j)==1:
            g[i-1][j-1]=1
            g[j-1][i-1]=1

dp[1][0]=1
for i in range(1,n):
    for j in range(21):
        if not i>>j&1:
            continue
        for k in range(21):
            if (not g[j][k]) or (i>>k&1):
                continue
            dp[i+(1<

上面的代码又再次提醒我：注意看题目啊！同时打开 Dev-C++ 做填空题是很有必要的！

七、试题F：时间显示

题目链接：蓝桥杯2021年第十二届省赛真题-时间显示 - C语言网

蓝桥杯保留节目，偶尔会有一道关于datetime的题目，注意用好help和dir即可，不多说，上代码。

#通过dir()、help()命令辅助完成了这一题
n=int(input())
days=n//(1000*60*60*24)
from datetime import *
t1=datetime(year=1970,month=1,day=1)
seconds=n//1000-days*24*60*60
micro=n-days*24*60*60*1000-seconds*1000
t2=(t1+timedelta(days,seconds,micro))
print("%02d:%02d:%02d"%(t2.hour,t2.minute,t2.second))

八、试题G：杨辉三角形

题目链接：蓝桥杯2021年第十二届省赛真题-杨辉三角形 - C语言网

这一题其实是道数学题，可以用递归、dp、打表等方式，但Python很奇怪，不知为何最多只能拿到40%的分数。

一些代码尝试。部分解释链接：【完美解析】蓝桥杯 省赛 杨辉三角形 python组 找规律+二分查找+组合数_蓝桥杯杨辉三角形python_愿此后再无WA的博客-CSDN博客

''' #递归直接超时严重,故后面改用dp
def f(n):
    if n==1 or n==0:
        return 1
    return n*f(n-1)

t=[1]
for i in range(1,1000):   
    for j in range(i+1):
        t.append(f(i)//(f(i-j)*f(j)))

N=int(input())
print(t.index(N)+1)
'''

''' #40%AC 还很容易段错误
dp=[[0]*2010 for _ in range(2010)]
dp[0][0]=1
dp[1][0]=dp[1][1]=1
t=[1,1,1]
for i in range(2,1200):   
    for j in range(0,i+1):
        if j==0 or j==i:
            t.append(1)
            dp[i][j]=1
            continue
        dp[i][j]=dp[i-1][j]+dp[i-1][j-1]
        t.append(dp[i][j])
        
N=int(input())
print(t.index(N)+1)
'''

# 打表大法！这才是最好用最接近比赛真实情况骗分的
# 首先先看看多少行会超过最大数据范围，经测试，34行足够了
# 打表竟然是30%，这是我想不通的，还不如dp的40%，可惜二分我没看懂
li = [[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1],[1, 6, 15, 20, 15, 6, 1], [1, 7, 21, 35, 35, 21, 7, 1], [1, 8, 28, 56, 70, 56, 28, 8, 1], 
      [1, 9, 36, 84, 126, 126, 84, 36, 9, 1], [1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1],
    [1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1], [1, 12, 66, 220, 495, 792, 924, 792, 495, 220, 66, 12, 1], 
    [1, 13, 78, 286, 715, 1287, 1716, 1716, 1287, 715, 286, 78, 13, 1],
    [1, 14, 91, 364, 1001, 2002, 3003, 3432, 3003, 2002, 1001, 364, 91, 14, 1], 
    [1, 15, 105, 455, 1365, 3003, 5005, 6435, 6435, 5005, 3003, 1365, 455, 105, 15, 1], 
    [1, 16, 120, 560, 1820, 4368, 8008, 11440, 12870, 11440, 8008, 4368, 1820, 560, 120, 16, 1], 
    [1, 17, 136, 680, 2380, 6188, 12376, 19448, 24310, 24310, 19448, 12376, 6188, 2380, 680, 136, 17, 1],
    [1, 18, 153, 816, 3060, 8568, 18564, 31824, 43758, 48620, 43758, 31824, 18564, 8568, 3060, 816, 153, 18, 1], 
    [1, 19, 171, 969, 3876, 11628, 27132, 50388, 75582, 92378, 92378, 75582, 50388, 27132, 11628, 3876, 969, 171, 19, 1], 
    [1, 20, 190, 1140, 4845, 15504, 38760, 77520, 125970, 167960, 184756, 167960, 125970, 77520, 38760, 15504, 4845, 1140, 190, 20, 1],
    [1, 21, 210, 1330, 5985, 20349, 54264, 116280, 203490, 293930, 352716, 352716, 293930, 203490, 116280, 54264, 20349, 5985, 1330, 210, 21, 1],
    [1, 22, 231, 1540, 7315, 26334, 74613, 170544, 319770, 497420, 646646, 705432, 646646, 497420, 319770, 170544, 74613, 26334, 7315, 1540, 231, 22, 1],
    [1, 23, 253, 1771, 8855, 33649, 100947, 245157, 490314, 817190, 1144066, 1352078, 1352078, 1144066, 817190, 490314, 245157, 100947, 33649, 8855, 1771, 253, 23, 1],
    [1, 24, 276, 2024, 10626, 42504, 134596, 346104, 735471, 1307504, 1961256, 2496144, 2704156, 2496144, 1961256, 1307504, 735471, 346104, 134596, 42504, 10626, 2024, 276, 24, 1],
    [1, 25, 300, 2300, 12650, 53130, 177100, 480700, 1081575, 2042975, 3268760, 4457400, 5200300, 5200300, 4457400, 3268760, 2042975, 1081575, 480700, 177100, 53130, 12650, 2300, 300, 25, 1],
    [1, 26, 325, 2600, 14950, 65780, 230230, 657800, 1562275, 3124550, 5311735, 7726160, 9657700, 10400600, 9657700, 7726160, 5311735, 3124550, 1562275, 657800, 230230, 65780, 14950, 2600, 325, 26, 1],
    [1, 27, 351, 2925, 17550, 80730, 296010, 888030, 2220075, 4686825, 8436285, 13037895, 17383860, 20058300, 20058300, 17383860, 13037895, 8436285, 4686825, 2220075, 888030, 296010, 80730, 17550, 2925, 351, 27, 1],
    [1, 28, 378, 3276, 20475, 98280, 376740, 1184040, 3108105, 6906900, 13123110, 21474180, 30421755, 37442160, 40116600, 37442160, 30421755, 21474180, 13123110, 6906900, 3108105, 1184040, 376740, 98280, 20475, 3276, 378, 28, 1],
    [1, 29, 406, 3654, 23751, 118755, 475020, 1560780, 4292145, 10015005, 20030010, 34597290, 51895935, 67863915, 77558760, 77558760, 67863915, 51895935, 34597290, 20030010, 10015005, 4292145, 1560780, 475020, 118755, 23751, 3654, 406, 29, 1],
    [1, 30, 435, 4060, 27405, 142506, 593775, 2035800, 5852925, 14307150, 30045015, 54627300, 86493225, 119759850, 145422675, 155117520, 145422675, 119759850, 86493225, 54627300, 30045015, 14307150, 5852925, 2035800, 593775, 142506, 27405, 4060, 435, 30, 1],
    [1, 31, 465, 4495, 31465, 169911, 736281, 2629575, 7888725, 20160075, 44352165, 84672315, 141120525, 206253075, 265182525, 300540195, 300540195, 265182525, 206253075, 141120525, 84672315, 44352165, 20160075, 7888725, 2629575, 736281, 169911, 31465, 4495, 465, 31, 1],
    [1, 32, 496, 4960, 35960, 201376, 906192, 3365856, 10518300, 28048800, 64512240, 129024480, 225792840, 347373600, 471435600, 565722720, 601080390, 565722720, 471435600, 347373600, 225792840, 129024480, 64512240, 28048800, 10518300, 3365856, 906192, 201376, 35960, 4960, 496, 32, 1],
    [1, 33, 528, 5456, 40920, 237336, 1107568, 4272048, 13884156, 38567100, 92561040, 193536720, 354817320, 573166440, 818809200, 1037158320, 1166803110, 1166803110, 1037158320, 818809200, 573166440, 354817320, 193536720, 92561040, 38567100, 13884156, 4272048, 1107568, 237336, 40920, 5456, 528, 33, 1],
    [1, 34, 561, 5984, 46376, 278256, 1344904, 5379616, 18156204, 52451256, 131128140, 286097760, 548354040, 927983760, 1391975640, 1855967520, 2203961430, 2333606220, 2203961430, 1855967520, 1391975640, 927983760, 548354040, 286097760, 131128140, 52451256, 18156204, 5379616, 1344904, 278256, 46376, 5984, 561, 34, 1]
    ]
def triangle(n):
    li1 = []
    length = len(li)
    for i in li:
        for j in i:
            li1.append(j) 
    # print(1)
    # print()
    while 1:
        if n in li1:
            print(li1.index(n) + 1)
            break


triangle(int(input()))

AC掉100%的二分+搜索！amazing，但是我还没看懂。

# 杨辉三角对称，只需看左半边
# 每行最大的数为 C(n, n // 2)，当n取33时有C(n, n // 2) > 1000000000
# 因此只需考虑0到33行,这个其实我们可以通过计算得出来
# 斜着看，会发现是递增序列，横着看，是严格递增序列
# 因此，如果在越里面的斜行中出现，则不会在外面的斜行中出现
# 需要从内向外搜索

def C(n, m):
    up = 1; down = 1
    t = n
    for i in range(1, min(m, n - m) + 1):  #这个min可以减少运算次数，即C(n,m)==C(n,n-m)
        up *= t; 
        t -= 1
        down *= i
    return up // down

n = int(input())

def search(i):
    l = i; 
    r = max(n, l); 
    k = i // 2       #正好是中间那个数
    while l < r:
        mid = l + r >> 1
        if C(mid, k) < n: 
           l = mid + 1
        else: 
           r = mid
    return l

for i in range(34, -1, -2):
    t = search(i)
    if C(t, i // 2) == n:
        print(t * (t + 1) // 2 + i // 2 + 1)
        break

九、试题H：左孩子右兄弟

题目链接：蓝桥杯2021年第十二届省赛真题-左孩子右兄弟 - C语言网

B站解析：SCUACM每日一题#73 左孩子右兄弟_哔哩哔哩_bilibili

直接看代码即可，因为思路比较简单，就是难想，直接深搜即可。

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=1e5+10;

int n;
int f[N];
vector G[N];

void add(int a,int b)
{
	G[a].push_back(b);
}

void dfs(int u){
	for(int i=0;i>n;
	for(int i=2,x;i<=n;i++)
	{
		cin>>x;
		add(x,i);
	}
//	cout<

等价Python代码，但是注意一个坑。

import sys
sys.setrecursionlimit(100000)  #不设置这个递归深度就会段错误，这个设置多深也是要考究一下的

N=100010
f=[0]*N
# G=[[]]*N    #这种定义和下面的定义方式不同，以后尽量用下面那种定义方式以免出现各种奇奇怪怪的bug
G=[[] for _ in range(N)]

def dfs(u:int):
    global G
    for i in range(len(G[u])):
        v=G[u][i]
        dfs(v)
        f[u]=max(f[u],f[v]+len(G[u]))  #怎么让新树的深度最深，选出最深的儿子放到最后连

n=int(input())
for i in range(2,n+1):
    x=int(input())
    G[x].append(i)

dfs(1)
print(f[1])

请注意：数组的定义方式要采取最稳的方法

十、试题I：异或数列

题目链接：蓝桥杯2021年第十二届省赛真题-异或数列 - C语言网

解释在代码中，这种题就体现草稿纸和笔的重要性了，细心一点查找规律，还是能搞到一点分的。

C++（AC）：

#include
#include
using namespace std;

void solve(){
	int n,cnt[25],maxp=0;
	memset(cnt,0,sizeof(cnt));
	cin>>n;
	for(int i=1;i<=n;i++){
		int p=0,t;
		cin>>t;
		while(t){
			cnt[p++]+=(t&1);
			maxp=max(p,maxp);
			t>>=1;
		}
	}
	int result=0;
	for(int i=maxp-1;i>=0;i--){
		if(cnt[i]&1){ //cnt[i] is 奇数 
			result=(n&1||cnt[i]==1)?1:-1;
			break; 
		}
	}
	printf("%d\n",result);
}

int main(){
	int T;
	cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

/*
由异或运算性质可知，二进制下每一位可以单独看，每一位之间互不影响。

两个数比大小，就是比谁的高位1更高。

因此我们统计每一位1的数量，然后从高位往低位看以比较大小。

1.假设在某一位，1的数量为偶数，那么无论怎么异或，Alice和Bob的数在这一位都是相同的。这时要到低一位继续检查；

2.假设在某一位，1只有一个，那么先手的Alice肯定会把这个1加给自己，Alice获胜，不需要继续往低位看了；

3.假设在某一位，1的数量为奇数（且大于1），那么拿到最后1个1的人获胜，此时考虑0的个数：

	a) 若0的个数为偶数（总数为奇数），Alice先手拿1，之后无论Bob拿什么，Alice跟着拿同样的数字（即Bob取1，Alice也取1；Bob取0，Alice也取0）。由于Alice拿走第一个1后，1和0都剩下偶数个，所以Alice一定可以拿到最后的1，即Alice必胜。

	b) 若0的个数为奇数（总数为偶数），Alice先手拿1则Bob拿0，Alice先手拿0则Bob拿1，第一轮结束后，留给先手的状态为1的个数和0的个数都为偶数，由3.1可知该状态为必败态（Bob只需模仿Alice即可保证自己拿到最后的1），即Bob必胜。

4.若所有位置检查完了，1的数量都是偶数，则是平局。

Python（75%）：

# 75%AC+25%运行超时
def solve():
    maxp=0
    cnt=[0 for _ in range(25)]
    # n=int(input())
    t=list(map(int,input().split()))
    for i in range(1,t[0]+1):
        p=0
        while t[i]:
            cnt[p]+=(t[i]&1)
            p+=1
            maxp=max(p,maxp)
            t[i]>>=1
    result=0
    for i in range(maxp-1,-1,-1):
        if cnt[i]&1:
            if t[0]&1 or cnt[i]==1:
                result=1
            else:
                result=-1
            break
            # result=(n&1)?1:-1
    print(result)

T=int(input())
for _ in range(T):
    solve()

同样的逻辑，Python会慢很多。

另外，这一题整数的数据范围到达 2^20！一看就是需要将二进制结合进来解题（<<,>>,&,|,~）。

十一、试题J：括号序列

题目链接：蓝桥杯2021年第十二届省赛真题-括号序列 - C语言网

这题另我很头大，看了很久虽说看懂题解了，但是正在比赛的时候99%我会敲不出来，dp的设置比较巧妙，唉，深深感到被大佬支配的恐惧。

acwing解释：3420. 括号序列 - AcWing题库

y总视频讲解：AcWing 3420. 括号序列（蓝桥杯C++ AB组辅导课） - AcWing

上面都是极好的教程解释，y总orz！

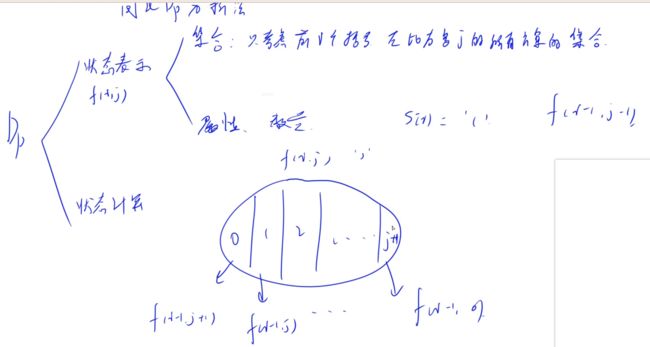
这里我就不再过多解释了，我自身重在理解。另外放上一张闫氏dp分析法的图。

代码C++：

#include 
#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int MOD=1000000007;
const int N=5010;
LL dp[N][N];
char str[N];
int len;
LL func()
{
    memset(dp,0,sizeof(dp));
    dp[0][0]=1;
    for(int i=1;i<=len;i++)//一个括号一个括号的判断
    {
        if(str[i]=='(')
        {
            for(int j=1;j<=len;j++)
            {
                dp[i][j]=dp[i-1][j-1];//不用考虑dp[i][0] 因为dp[i-1][-1]是不合法的情况 不存在 为0
            }
        }
        else
        {
            dp[i][0]=(dp[i-1][0]+dp[i-1][1])%MOD;//特判防止越界 这里数据短，用的是优化前的推断
            for(int j=1;j<=len;j++)
            {
                 dp[i][j]=(dp[i-1][j+1] + dp[i][j-1])%MOD;
            }
        }
    }
    for(int i=0;i<=len;i++)
        if(dp[len][i]) return dp[len][i];//我们需要的就是长度为len添加括号的合法情况，而从前往后遍历出现的第一个有可能的情况就是需要括号数最少的情况，因为左括号可以加很多个，我们仅需添加最少的情况
        return -1;
}
int main()
{
    scanf("%s",str+1);//从下标为1开始
    len=strlen(str+1);
    LL l=func();
    reverse(str+1,str+len+1);
    for(int i=1;i<=len;i++)
    {
        if(str[i]=='(') str[i]=')';
        else str[i]='(';
    }
    LL r=func();
    cout<

省赛中这种题不要就算了，做不出来的话，能骗点分就骗点分，不能也不强求，争取把前面的题都拿下一定的分数。 

 

以上，第十二届蓝桥杯省赛Python大学组复盘

祝好