蚁群优化算法

目录

蚁群优化

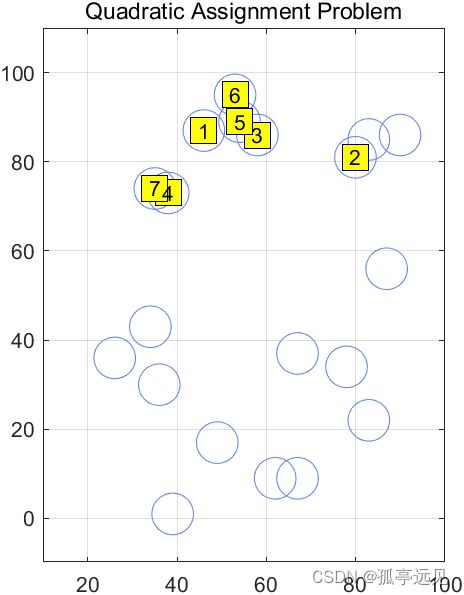
Quadratic Assignment Problem (QAP)

 主要代码

create model

Cost

RouletteWheelSelection

Plot

结果

---

蚁群优化

---

        蚁群优化（ACO）是一套概率元启发法和智能优化算法，其灵感来源于蚂蚁的社会行为。ACO算法也被归类为群集智能方法，因为在这些算法的结构中通过模拟蚂蚁的行为来实现这一范式。

---

Quadratic Assignment Problem (QAP)

        二次分配问题

---

 主要代码

---

clc;
clear;
close all;

%% Problem Definition

model = CreateModel();

CostFunction = @(p) MyCost(p, model);

nVar = model.n;

%% ACO Parameters

MaxIt = 500;      % Maximum Number of Iterations

nAnt = 50;        % Number of Ants (Population Size)

Q = 1;

tau0 = 10;        % Initial Phromone

alpha = 0.3;      % Phromone Exponential Weight 弗罗蒙指数权重

rho = 0.1;        % Evaporation Rate 蒸发率


%% Initialization

tau = tau0*ones(model.m, nVar);

BestCost = zeros(MaxIt, 1);    % Array to Hold Best Cost Values

% Empty Ant
empty_ant.Tour = [];
empty_ant.Cost = [];

% Ant Colony Matrix
ant = repmat(empty_ant, nAnt, 1);

% Best Ant
BestSol.Cost = inf;


%% ACO Main Loop

for it = 1:MaxIt
    
    % Move Ants
    for k = 1:nAnt
        
        ant(k).Tour = [];
        
        for l = 1:nVar
            
            P = tau(:, l).^alpha;
            
            P(ant(k).Tour) = 0;
            
            P = P/sum(P);
            
            j = RouletteWheelSelection(P);
            
            ant(k).Tour = [ant(k).Tour j];
            
        end
        
        ant(k).Cost = CostFunction(ant(k).Tour);
        
        if ant(k).Cost

---

create model

---

function model = CreateModel()

    x = [67 80 62 34 54 36 53 46 39 35 83 58 87 90 83 38 26 78 49 67];
    
    y = [9 81 9 43 89 30 95 87 1 74 85 86 56 86 22 73 36 34 17 37];
    
    m = numel(x);
    
    d = zeros(m, m);
    for p = 1:m-1
        for q = p+1:m
            d(p, q) = sqrt((x(p)-x(q))^2+(y(p)-y(q))^2);
            d(q, p) = d(p, q);
        end
    end
    
    w = [0    6    6    3    5    5    5
       6    0    6    4  -10    3    6
       6    6    0    4    5    8    6
       3    4    4    0    4    4  100
       5  -10    5    4    0    3    4
       5    3    8    4    3    0    4
       5    6    6  100    4    4    0];

    n = size(w, 1);
    
    model.n = n;
    model.m = m;
    model.w = w;
    model.x = x;
    model.y = y;
    model.d = d;
    
end

---

Cost

---

function z = MyCost(p, model)

    n = model.n;
    w = model.w;
    d = model.d;

    z = 0;
    
    for i = 1:n-1
        for j = i+1:n
            
            z = z+w(i, j)*d(p(i), p(j));
            
        end
    end

end

---

RouletteWheelSelection

---

cumsum 累积和

B = cumsum(A) 从 A 中的第一个其大小不等于 1 的数组维度开始返回 A 的累积和。

• 如果 A 是向量，则 cumsum(A) 返回包含 A 元素累积和的向量。

• 如果 A 是矩阵，则 cumsum(A) 返回包含 A 每列的累积和的矩阵。

• 如果 A 为多维数组，则 cumsum(A) 沿第一个非单一维运算。

B = cumsum(A,dim) 返回沿维度 dim 的元素的累积和。例如，如果 A 是矩阵，则 cumsum(A,2) 返回每行的累积和。

B = cumsum(___,direction) 可选择性地使用上述任何语法指定方向。必须指定 A，也可以指定 dim。例如，cumsum(A,2,'reverse') 通过从尾到头计算 A 的第二个维度返回其中各行的累积和。

B = cumsum(___,nanflag) 指定在上述任意语法的计算中包括还是忽略 NaN 值。cumsum(A,'includenan') 会在计算中包括所有 NaN 值，而 cumsum(A,'omitnan') 则忽略这些值。

find 查找

k = find(X) 返回一个包含数组 X 中每个非零元素的线性索引的向量。

• 如果 X 为向量，则 find 返回方向与 X 相同的向量。

• 如果 X 为多维数组，则 find 返回由结果的线性索引组成的列向量。

k = find(X,n) 返回与 X 中的非零元素对应的前 n 个索引。

k = find(X,n,direction)（其中 direction 为 'last'）查找与 X 中的非零元素对应的最后 n 个索引。direction 的默认值为 'first'，即查找与非零元素对应的前 n 个索引。

function j = RouletteWheelSelection(P)

    r = rand;
    
    C = cumsum(P);
    
    j = find(r <= C, 1, 'first');

end

---

Plot

---

function PlotSolution(p, model)

    x = model.x;
    y = model.y;
    
    plot(x, y, 'o', 'MarkerSize', 20, 'Color', [0.4 0.5 0.9]);
    
    hold on;
    
    plot(x(p), y(p), 'sk', 'MarkerSize', 16, 'MarkerFaceColor', 'y');
    
    n = model.n;
    for i = 1:n
        text(x(p(i)), y(p(i)), num2str(i), ...
            'HorizontalAlignment', 'center', ...
            'VerticalAlignment', 'middle');
    end
    
    title('Quadratic Assignment Problem');
    
    hold off;
    axis equal;
    grid on;
    
    alpha = 0.1;
    
    xmin = min(x);
    xmax = max(x);
    dx = xmax - xmin;
    xmin = floor((xmin - alpha*dx)/10)*10;
    xmax = ceil((xmax + alpha*dx)/10)*10;
    xlim([xmin xmax]);
    
    ymin = min(y);
    ymax = max(y);
    dy = ymax - ymin;
    ymin = floor((ymin - alpha*dy)/10)*10;
    ymax = ceil((ymax + alpha*dy)/10)*10;
    ylim([ymin ymax]);

end

---

结果

---

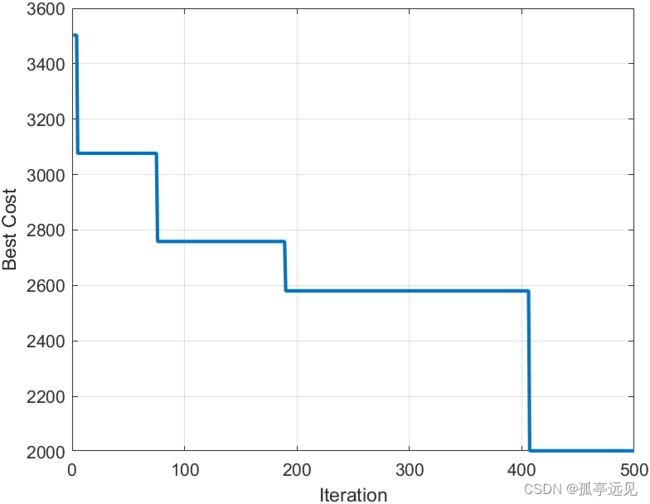
Iteration 500: Best Cost = 2003.5414