Kaggle数据竞赛-房价预测

Kaggle数据竞赛-房价预测

赛事介绍

这是Kaggle上一个非常适合新手入门的比赛，总共有79 个解释变量，描述了爱荷华州埃姆斯住宅的各个方面，选手需要预测每套房屋的最终价格。
从任务内容上看，这是一个简单的回归任务，但是如果想要获得高分，前期的数据探索与特征工程是必不可少的。笔者参考了诸多大佬的博客，构建了最终的方案，目前的结果在Kaggle上大致在前10%左右。

实战流程

笔者将尽可能地描述清楚此赛事的整体流程，包括数据探索分析、数据预处理、特征工程、模型构建与评估、结果注册五个重要环节。

数据探索分析

当我们分析清楚了比赛的任务类型后，首先要做的就是对数据进行探索性分析，主要包括缺失值分析、相关性分析、异常值分析、特征分布分析等。

相关库导入

import warnings
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import stats
from scipy.stats import norm,skew
from scipy.special import boxcox1p
from scipy.stats import boxcox_normmax
from sklearn.linear_model import Ridge, RidgeCV, ElasticNet, LassoCV, LassoLarsCV
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor
from lightgbm import LGBMRegressor
from xgboost import XGBRegressor
from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import KFold, GridSearchCV, cross_val_score, train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# Comment this if the data visualisations doesn't work on your side
%matplotlib inline

数据集加载

train_file_path = "../input/house-prices-advanced-regression-techniques/train.csv"
train = pd.read_csv(train_file_path)
test_file_path = "../input/house-prices-advanced-regression-techniques/test.csv"
test = pd.read_csv(test_file_path)
print("Full train dataset shape is {}".format(train.shape))
print("Full test dataset shape is {}".format(test.shape))
train.head(3), test.head(3)

我们可以发现数据集里有一个ID列，其实是没有带任何业务含义的，可以先删除掉。同时为了方便，我们也可以将训练集和测试集数据合并在一起后做分析处理工作。

train.drop("Id", axis = 1, inplace = True)
test.drop("Id", axis = 1, inplace = True)

ntrain = train.shape[0]
ntest = test.shape[0]
y_train = train.SalePrice.values
dataset_df = pd.concat((train, test)).reset_index(drop=True)
dataset_df.drop(['SalePrice'], axis=1, inplace=True)
print("all_data size is : {}".format(dataset_df.shape))
dataset_df.head(3)

我们将预测价格列单独拎出来后，可以看到还剩下了79个特征。数据准备好后，我们就可以进行后续的数据分析了。

缺失值分析

我们可以先将有缺失值的特征筛选出来，看看整体情况如何。

# check the null ratio
null_per = dataset_df.isnull().sum() / dataset_df.shape[0]
null_per[null_per > 0].sort_values(ascending=False)

我们可以发现有6个特征的缺失值比例较高。通常来讲，对于缺失值的处理方式包括删除行/列、数值型的特征可以进行均值/中位数填充、文本型的特征可以使用None填充作为缺失特征。
这6个特征的业务语义如下所示：

• PoolQC：游泳池质量，如果为空代表没有
• MiscFeature：其他类别没有覆盖的功能，比如电梯等，如果为空代表没有
• Alley：小巷类型，如果为空代表没有
• Fence：围栏，如果为空代表没有
• FireplaceQu：壁炉质量，如果为空代表没有
• LotFrontage：相连的街道尺寸，为空的话可以通过均值/中位数填充

相关性分析

在做完缺失值分析后，我们可以看看各个特征与价格之间的相关性如何，以便我们选择出比较重要的特征进行分布探索与异常值分析。

fig = plt.figure(figsize=(12,8))
abs(train.corr()['SalePrice']).sort_values(ascending=False).plot.bar()
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)

异常值分析

我们可以选择前4个与房价相关性较高的特征，再加上YearBuilt（房子建造的年份）特征一起，通过散点图的形式看看数据关系。

figure=plt.figure(figsize=(12, 8))
sns.pairplot(x_vars=['OverallQual','GrLivArea','GarageArea','TotalBsmtSF', 'YearBuilt'],y_vars=['SalePrice'],
             data=train,dropna=True,size=5,kind="reg")
plt.show()

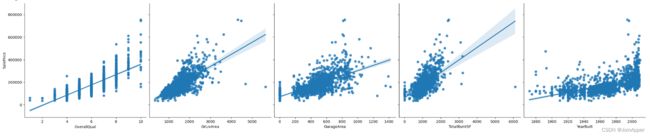
从中可以发现这五个特征和价格均呈现出了正向线性关系，但是存在部分异常点，需要后续进行清洗，比如在GarageArea的散点图中，我们能明显看见部分数据存在面积更大，价格更低的异常现象。

数值型特征分布分析

除了主要特征与价格的散点分布图外，我们还可以将所有的数值型特征拎出来看看分布情况。

df_num = dataset_df.select_dtypes(include = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64'])
df_num.head(3)

我们可以发现有一些特征的分布相比于标准正态分布是有一定偏差的，后续也可以进行处理。

价格分布分析

除了做特征的分布分析外，我们还可以看看预测价格的分布情况。

sns.distplot(y_train,fit=norm);
(mu,sigma) = norm.fit(y_train)
print('mu = {:.2f} and sigma = {:.2f}'.format(mu,sigma))
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

可以发现价格也不完全满足标准正态分布，后续一并进行处理。

数据预处理

在经过上面的数据探索性分析后，我们发现还需要进行一些数据预处理工作才能喂给模型进行训练，包括缺失值填充、异常数据清洗、数值型特征分布纠正、价格分布纠正。

缺失值填充

从之前的分析中，我们可以知道某些特征的缺失值是由于其不存在而导致的，因此可以将缺失作为一个特征。而对于其他数值缺失值，我们可以选择填充为0、中位数、均值等。

# process null value
cols1 = ["PoolQC" , "MiscFeature", "Alley", "Fence", "FireplaceQu", "GarageQual", "GarageCond", "GarageFinish", "GarageYrBlt", "GarageType", "BsmtExposure", "BsmtCond", "BsmtQual", "BsmtFinType2", "BsmtFinType1", "MasVnrType"]
for col in cols1:
    dataset_df[col].fillna("None", inplace=True)
    
cols=["MasVnrArea", "BsmtUnfSF", "TotalBsmtSF", "GarageCars", "BsmtFinSF2", "BsmtFinSF1", "GarageArea", 
"MSZoning", "Utilities", "Exterior1st", "Exterior2nd", "Electrical", "BsmtFullBath", "BsmtHalfBath", "KitchenQual", "Functional", "SaleType"]
for col in cols:
    dataset_df[col].fillna(0, inplace=True)
    
dataset_df["LotFrontage"] = dataset_df.groupby("Neighborhood")["LotFrontage"].transform(lambda x:x.fillna(x.median()))

异常值清洗

综合上面的分析，我们可以按照以下方式清洗训练集的异常值。

train = train.drop(train[(train['OverallQual']<5) &
                                        (train['SalePrice']>200000)].index)
 
train = train.drop(train[(train['GrLivArea']>4000) &
                                        (train['SalePrice']<300000)].index)
 
train = train.drop(train[(train['YearBuilt']<1900) &
                                        (train['SalePrice']>400000)].index)

train = train.drop(train[(train['TotalBsmtSF']>6000) &
                                        (train['SalePrice']<200000)].index)

train = train.drop(train[(train['GarageArea']>1200) &
                                        (train['SalePrice']<200000)].index)                                   

此时再调用图形绘制代码，可以看到异常值基本已经被清洗了。

figure=plt.figure(figsize=(12, 8))
sns.pairplot(x_vars=['OverallQual','GrLivArea','GarageArea','TotalBsmtSF', 'YearBuilt'],y_vars=['SalePrice'],
             data=train,dropna=True,size=5,kind="reg")
plt.show()

特征分布修正

从探索性分析中，我们也可以发现部分特征存在分布偏离的情况，因此可以选择偏度比较高的特征进行纠正。

numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric = []
for i in dataset_df.columns:
    if dataset_df[i].dtype in numeric_dtypes and i != 'SalePrice':
        numeric.append(i)
        
skew_all_data = dataset_df[numeric].apply(lambda x:skew(x)).sort_values(ascending=False)
high_skew = skew_all_data[skew_all_data>0.15]
skew_index = high_skew.index
print('There are {} numeric features with skew>0.15'.format(high_skew.shape[0]))
skewness = pd.DataFrame({'Skew':high_skew})
skew_all_data.head(20)

for i in skew_index:
    dataset_df[i] = boxcox1p(dataset_df[i],boxcox_normmax(dataset_df[i]+1))

价格分布修正

上面的特征我们使用了boxcox的方式修正，针对价格我们可以尝试采用取对数的方式。

y_train = np.log1p(y_train)

sns.distplot(y_train , fit=norm);

(mu, sigma) = norm.fit(y_train)
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

特征工程

在做完初步的数据预处理后，便是重要的特征工程环节了，主要做的事情包括类别特征编码，新增特征等。

类别特征编码

我们可以将类别特征的值映射为数字，方便后面的模型训练与预测。

dataset_df = dataset_df.replace({'Street': {'Pave': 1, 'Grvl': 0 },
                             'FireplaceQu': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1,
                                            'NoFireplace': 0
                                            },
                             'Fence': {'GdPrv': 2,
                                       'GdWo': 2,
                                       'MnPrv': 1,
                                       'MnWw': 1,
                                       'NoFence': 0},
                             'ExterQual': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1
                                            },
                             'ExterCond': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1
                                            },
                             'BsmtQual': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1,
                                            'NoBsmt': 0},
                             'BsmtExposure': {'Gd': 3,
                                            'Av': 2,
                                            'Mn': 1,
                                            'No': 0,
                                            'NoBsmt': 0},
                             'BsmtCond': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1,
                                            'NoBsmt': 0},
                             'GarageQual': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1,
                                            'NoGarage': 0},
                             'GarageCond': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1,
                                            'NoGarage': 0},
                             'KitchenQual': {'Ex': 5,
                                            'Gd': 4,
                                            'TA': 3,
                                            'Fa': 2,
                                            'Po': 1},
                             'Functional': {'Typ': 0,
                                            'Min1': 1,
                                            'Min2': 1,
                                            'Mod': 2,
                                            'Maj1': 3,
                                            'Maj2': 4,
                                            'Sev': 5,
                                            'Sal': 6},
                             'CentralAir': {'Y': 1,
                                            'N': 0},
                             'PavedDrive': {'Y': 1,
                                            'P': 0,
                                            'N': 0} 
                            })

新增特征

与此同时，通过对业务特征的分析，可以通过常见的加减乘除添加新的特征。

#基于业务理解增加特征
#地下室面积总面积
dataset_df['TotalBSF'] = (dataset_df['TotalBsmtSF']+dataset_df['1stFlrSF']+dataset_df['2ndFlrSF']+dataset_df['BsmtUnfSF'])
#全屋浴室加总
dataset_df['Total_Bathrooms'] = (dataset_df['FullBath']+(0.5*dataset_df['HalfBath'])+dataset_df['BsmtFullBath']+(0.5*dataset_df['BsmtHalfBath']))
#门廊加总
dataset_df['Total_porch_sf'] = (dataset_df['OpenPorchSF'] + dataset_df['3SsnPorch'] + dataset_df['EnclosedPorch'] + dataset_df['ScreenPorch'] + dataset_df['WoodDeckSF'])
#车库面积加总
dataset_df['Total_Garage'] = dataset_df['GarageArea']+ dataset_df['GarageCars'] 
#外部有关面积数据加总
dataset_df['Outside_Area'] = dataset_df['Total_porch_sf'] + dataset_df['PoolArea']
#屋内全部楼层加地下室面积加总
dataset_df['Total_sqr'] = (dataset_df['TotalBSF'] + dataset_df['LowQualFinSF'] + dataset_df['1stFlrSF'] + dataset_df['2ndFlrSF'])
#减法
#建造，售卖时间间隔
dataset_df['YearsSinceRemodel'] = dataset_df['YrSold'].astype(int) - dataset_df['YearBuilt'].astype(int)
#改建，售卖时间间隔
dataset_df['YearsSinceRemodel'] = dataset_df['YrSold'].astype(int) - dataset_df['YearRemodAdd'].astype(int)   

当然可能还有其他类别特征没有做转换的，通过get_dummies转换为新特征，最后可以得到396列特征（后面还可以对这些特征做一下筛选）。

dataset_df = pd.get_dummies(dataset_df) 
dataset_df.head(3)

模型构建与评估

做完上述的特征工程后，我们就可以进行模型构建与评估了。

训练测试集分隔

由于之前我们将训练数据集和测试数据集合并在了一起，在喂给模型之前首先要进行分离。

clean_train = dataset_df[:ntrain]
clean_test = dataset_df[ntrain:]
clean_train = pd.concat([clean_train, pd.Series(y_train, name='SalePrice')], axis=1)
clean_train.shape,clean_test.shape

模型训练与预测

# 定义评价指标
def rmse_cv(model):
    rmse= np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv = 5))
    return(rmse)

X = clean_train.drop(columns='SalePrice')
y = clean_train['SalePrice']
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=10)
# 定义交叉验证模式
kf = KFold(n_splits=10, random_state=50, shuffle=True)

warnings.filterwarnings('ignore')
# 建立基线模型
lgb = LGBMRegressor(objective='regression', random_state=50)
xgb = XGBRegressor(objective='reg:squarederror',random_state=50)
ridge = make_pipeline(RobustScaler(), RidgeCV(cv=kf))
svr = make_pipeline(RobustScaler(), SVR())
gbr = GradientBoostingRegressor(random_state=50)
rf = RandomForestRegressor(random_state=50)

# 基线模型评估
models = [lgb, xgb, ridge, svr, gbr, rf]
model_names = ['lgb','xgb','ridge','svr','gbr','rf']
scores = {}

for i, model in enumerate(models):
    score = rmse_cv(model)
    print('{} rmse score: {:.4f}, rmse std: {:.4f}'.format(model_names[i], score.mean(), score.std()))
    scores[model_names[i]] = (score.mean(), score.std())
    
rmse_df = pd.DataFrame(scores, index=['rmse_score','rmse_std'])
rmse_df.sort_values('rmse_score', axis=1, inplace=True)
rmse_df

模型Stacking

模型融合是目前提高分数的有效利器之一，我们可以选择上述的模型作为基准模型，用xgb作为二层模型预测最终的价格。

class StackingRegressor(object):
    
    def __init__(self, fir_models, fir_model_names, sec_model, cv):
        # 第一层的基模型
        self.fir_models = fir_models
        self.fir_model_names = fir_model_names
        # 第二层用来预测结果的模型
        self.sec_model = sec_model
        # 交叉验证模式，必须为k_fold对象
        self.cv = cv
    
    def fit_predict(self, X, y, test):    # X,y,test必须为DataFrame
        # 创建空DataFrame
        stacked_train = pd.DataFrame()
        stacked_test = pd.DataFrame()
        # 初始化折数
        n_fold = 0

        # 遍历每个模型，做交叉验证
        for i, model in enumerate(self.fir_models):
            # 初始化stacked_train
            stacked_train[self.fir_model_names[i]] = np.zeros(shape=(X.shape[0], ))

            #遍历每一折交叉验证
            for train_index, valid_index in self.cv.split(X):
                # 初始化stacked_test
                n_fold += 1
                stacked_test[self.fir_model_names[i] + str(n_fold)] = np.zeros(shape=(test.shape[0], ))

                # 划分数据集
                X_train, y_train = X.iloc[train_index, :], y.iloc[train_index]
                X_valid, y_valid = X.iloc[valid_index, :], y.iloc[valid_index]

                # 训练模型并预测结果
                model.fit(X_train, y_train)
                stacked_train.loc[valid_index, self.fir_model_names[i]] = model.predict(X_valid)
                stacked_test.loc[:, self.fir_model_names[i] + str(n_fold)] = model.predict(test)
            print('{} is done.'.format(self.fir_model_names[i]))

        # stacked_train加上真实值标签
        y.reset_index(drop=True, inplace=True)
        stacked_train['y_true'] = y

        # 计算stacked_test中每个模型预测结果的平均值
        for i, model_name in enumerate(self.fir_model_names):
            stacked_test[model_name] = stacked_test.iloc[:, :10].mean(axis=1)
            stacked_test.drop(stacked_test.iloc[:, :10], axis=1, inplace=True)
        
        # 打印stacked_train和stacked_test
        print('----stacked_train----\n', stacked_train)
        print('----stacked_test----\n', stacked_test)
        
        # 用sec_model预测结果
        self.sec_model.fit(stacked_train.drop(columns='y_true'), stacked_train['y_true'])
        y_pred = self.sec_model.predict(stacked_test)
        return y_pred
    
sr = StackingRegressor(models, model_names, xgb, kf)
stacking_pred = sr.fit_predict(Xtrain, ytrain, Xtest)

def rmse(y, y_pred):
    rmse = np.sqrt(mean_squared_error(y, y_pred))
    return rmse

stacking_score = rmse(ytest, stacking_pred)
print(stacking_score)

模型均值融合

当然除了stack方式，也可以选择对各个模型预测结果进行加权融合。

def blending(X, y, test):
    lgb.fit(X, y)
    lgb_pred = lgb.predict(test)

    xgb.fit(X, y)
    xgb_pred = xgb.predict(test)
    
    ridge.fit(X, y)
    ridge_pred = ridge.predict(test)
    
    svr.fit(X, y)
    svr_pred = svr.predict(test)
    
    gbr.fit(X, y)
    gbr_pred = gbr.predict(test)
    
    rf.fit(X, y)
    rf_pred = rf.predict(test)
    
    sr = StackingRegressor(models, model_names, xgb, kf)
    sr_pred = sr.fit_predict(X, y, test)
    
    # 加权求和
    blended_pred = (0.05 * lgb_pred +
                    0.1 * xgb_pred +
                    0.2 * ridge_pred +
                    0.25 * svr_pred +
                    0.15 * gbr_pred +
                    0.05 * rf_pred +
                    0.2 * sr_pred)
    return blended_pred

blended_pred = blending(Xtrain, ytrain, Xtest)
blending_score = rmse(ytest, blended_pred)
print(blending_score)

结果注册

最后我们可以选择加权融合的方式进行结果提交，这里不要忘记对价格做对数反变换。

sample_submission_df = pd.read_csv('../input/house-prices-advanced-regression-techniques/sample_submission.csv')
sample_submission_df['SalePrice'] = np.exp(blending(X, y, clean_test)) - 1
sample_submission_df.to_csv('/kaggle/working/submission.csv', index=False)
sample_submission_df.head()

总结与反思

通过这次比赛的学习，算是初步了解了kaggle的整个流程。
但是整个流程看下来，还是有很多不足的地方：

1. 特征工程其实做得不够，特征太多了，可以做一下特征选择的工作
2. 模型也没有经过调参验证
3. 只是用了传统的机器学习模型，没有尝试深度学习模型，或许能减除特征工程这步

如果有时间的话，可以再做一下后续的工作。

参考文档

Kaggle竞赛–房价预测
Kaggle竞赛 —— 房价预测 (House Prices)