【算法】ijk矩阵乘法性能分析

ijk矩阵乘法性能分析

1. Problem description

• 利用文件模拟cache缓存机制读写数据，将二维数组存储到文件中，并模拟对矩阵进行读写操作。操作要求为读取矩阵A、B，并输出A、B的乘积C。
• 改变cache大小
• 改变读取数据的顺序，即ijk、ikj
• 分析cache miss的次数与cache大小、读取数据顺序之间的关系

2. Algorithom idea

为了简化思路，我们可以先想想若二维数组在内存中是如何计算的，显而易见，当计算C=A*B

以ikj的顺序进行的时候，有：

for(int i=0;i<n;i++)
    for(int k=0;k<n;k++)
        for(int j=0;j<n;j++){
             c[i][j] += a[i][k] * b[k][j];
        }

我们可以在此基础上进行代理函数设计，将计算函数变为如下形式：

for(int i=0;i<n;i++)
    for(int k=0;k<n;k++)
        for(int j=0;j<n;j++){
            C.set(i,j,B.get(k,j)*A.get(i,k)+ C.get(i,j));
        }

因此我们要做的就是进行set、get函数的设计。

2.1 get函数设计思路

为了简化文件查找操作，我们在文件中没有必要以二维的形式存储数据，可以通过数学的方法将二维数组转换成一维数组，即：targetIndex = row * rowSize + col 。

我们只需要用两个变量记录目前 Cache 存储的下表范围（ startIndex , endIndex ）即可判断访存Cache访问是否命中——如果不在该范围内，直接去文件中读取 （targetIndex, targetIndex+cacheSize）对cache进行更新即可。

2.2 set函数设计思路

同get函数的实现思路类似，将二维下标变为一维记录。但是需要考虑脏位——当targetIndex不在cache中时，不能直接覆盖cache，而需要将在cache中已经被更改过的数据写回更新进外存，即文件中。

此处由于每次更新都是以一整个cache为单位，因此我们只为外存设置一个脏位，而不是为每个Unit设置。当dirty==true时，表明之前有一次 set 调用命中，对与外存映射的cache中数据进行修改。

3 Function model design

3.1 Matrix类实现

    //缓存数组
    int[] cache;
    //矩阵的行数
    int rowSize;
    //矩阵列数
    int colSize;
    //缓存开始的行数
    int startRow;
    //缓存开始的列数
    int startCol;
    //缓存结束的行数
    int endRow;
    //缓存结束的列数
    int endCol;
    //缓存大小
    int cacheSize;
    //cache miss 次数
    long cacheMissCount;
    //cache 访问次数
    long cacheCount;
    //矩阵在磁盘中的位置
    String matrixFilePath;
    //缓存是否被写入过
    Boolean dirty;
    //是否整个矩阵都在内存当中

    Matrix(int rowSize,int colSize,int cacheSize,String matrixFilePath) throws IOException {
        this.colSize=colSize;
        this.rowSize=rowSize;
        this.cacheSize=cacheSize;
        this.matrixFilePath=matrixFilePath;
        cache=new int[cacheSize];
        dirty=false;
        endRow=-1;
        endCol=-1;
        File file=new File(matrixFilePath);
        file.delete();
        file.createNewFile();
        createRandomMatrix();
    }

3.2 get函数实现

int get(int row, int col)
{
    if (row > rowSize || col > colSize)
        try {
            throw new Exception("row > rowSize || col > this->colSize");
        } catch (Exception e) {
            e.printStackTrace();
        }
    cacheCount++;
    if (currentIndex(startRow, startCol) <= currentIndex(row, col) && currentIndex(row, col) <= currentIndex(endRow, endCol))
        return cache[currentIndex(row, col) - currentIndex(startRow, startCol)];
    else
    {
        cacheMissCount++;
        readCache(row, col);
        return cache[0];
    }
}

void writeCache()
    {
        RandomAccessFile raf=null;
        try{
            raf = new RandomAccessFile(new File(matrixFilePath), "rw");
            raf.seek((currentIndex(startRow, startCol)) * 4);
            for (int i = 0; i < cacheSize; i++)
            {
                raf.writeInt(cache[i]);
            }
        }catch (Exception e){
            e.printStackTrace();
        }finally {
            try {
                raf.close();
            }catch (IOException e){
                e.printStackTrace();
            }
        }
    }

3.3 set函数实现

void set(int row, int col, int value)
{
    if (row > rowSize || col > colSize)
        try {
            throw new Exception ("row > rowSize || col > this->colSize");
        } catch (Exception e) {
            e.printStackTrace();
        }
    if (currentIndex(startRow, startCol) <= currentIndex(row, col) && currentIndex(row, col) <= currentIndex(endRow, endCol))
        cache[currentIndex(row, col) - currentIndex(startRow, startCol)] = value;
    else
    {
        cacheMissCount++;
        readCache(row, col);
        cache[0] = value;
    }
    dirty = true;
}

    void readCache(int row, int col)
    {
        if (dirty)
        {
            writeCache();
            dirty = false;
        }
        RandomAccessFile raf=null;
        try{
            raf = new RandomAccessFile(new File(matrixFilePath), "r");
            raf.seek((currentIndex(row, col)) * 4);
            for (int i = 0; i < cacheSize; i++){
                //未知错误,暂时笨方法
                if(raf.getFilePointer()+1>=raf.length())break;
              cache[i]=raf.readInt();
            }

            startRow = row;
            startCol = col;
            endRow = cacheSize / rowSize + startRow;

            if ((cacheSize % rowSize - 1 + startCol) > colSize)
            {
                endRow++;
                endCol = cacheSize % rowSize - 1 + startCol - colSize;
            }
            else
            {
                endCol = cacheSize % rowSize - 1 + startCol;
            }
        }catch (Exception e){
            e.printStackTrace();
        }finally {
            try {
                raf.close();
            }catch (IOException e){
                e.printStackTrace();
            }
        }
    }

4. Test results and analysis

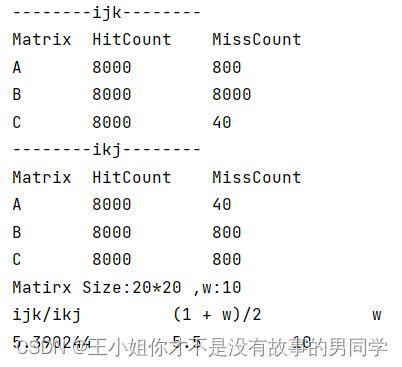
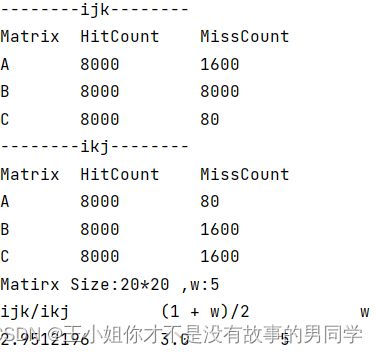
以下是实验结果截图：

以下是理论值分析：

将理论值和实验值比较，发现基本吻合。

5. Project summary

在本次实验中，最大的困难是如何通过文件读写操作来模拟cache机制。在文件中，需要找到定义文件上一次读写位置的方法，在每次cache miss后找到该位置再进行读写。我的方法是使用一行来表式一个矩阵，并且通过记录矩阵读取的位置来定位文件的位置。