动态规划-背包问题（三）

该题是lintcode上的 440 · 背包问题 III算法题，该题的解题思路是按照九章侯老师给的方法去实现的。

1 描述

给定 n 种物品, 每种物品都有无限个. 第 i 个物品的体积为 A[i], 价值为 V[i].

再给定一个容量为 m 的背包. 问可以装入背包的最大价值是多少?

不能将一个物品分成小块.
放入背包的物品的总大小不能超过 m.

2 样例

2.1 样例 1:

输入: A = [2, 3, 5, 7], V = [1, 5, 2, 4], m = 10
输出: 15
解释: 装入三个物品 1 (A[1] = 3, V[1] = 5), 总价值 15.

2.2 样例 2:

输入: A = [1, 2, 3], V = [1, 2, 3], m = 5
输出: 5
解释: 策略不唯一. 比如, 装入五个物品 0 (A[0] = 1, V[0] = 1).

3 算法解题思路以及实现方法

3.1 算法解题思路

3.1.1 确定状态

该算法题和背包问题（二）不同的点是每种物品有无穷多个。
其解题思路也和背包问题（二）很类似。

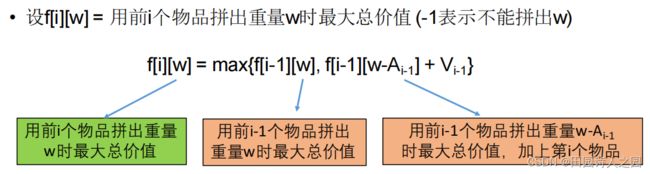
3.1.2 转移方程

因为每个物品有无穷多个，所以Ai有无穷多个，既，可以用0个Ai, 1个Ai, 2个 Ai,…

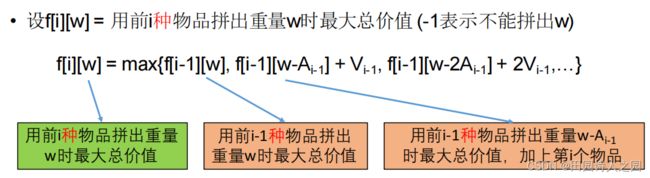
3.1.3 初始条件以及边界情况

设：f[i][]j表示用前i个物品拼出重量为j时的最大总价值（-1表示不能拼出j）
f[i][w] = max{f[i-1][w], f[i][w-Ai-1] + Vi-1 | w≥Ai-1 且f[i][w-Ai-1] ≠-1}
初始条件：
f[0][0] = 0，表示0个物品可以拼出重量为0，最大总价值为0
f[0][1…M] = -1，表示0个物品不能拼出重量大于0的重量
边界情况：
f[i][j - Ai-1]只能在j >= Ai-1，并且f[i][j - Ai-1] != -1时使用

3.1.4 计算顺序

初始化f[0][0], f[0][1], …, f[0][M]

计算前1个物品可以拼出各种重量的最大总价值：f[1][0], f[1][1], …, f[1][M]

…

计算前N个物品拼出各种重量的最大价值：f[N][0], f[N][2], …, f[N][M]

最后结果为：max0<=j<=M{f[N][j] | f[N][j] ≠-1}

时间复杂度为：O(MN)

空间复杂度为：O(MN)

空间优化后的复杂度为：O(M)

3.2 算法实现

3.2.1 java实现的O(MN)算法复杂度

public class Solution {
    /**
     * @param a: an integer array
     * @param v: an integer array
     * @param m: An integer
     * @return: an array
     */
    public int backPackIII(int[] a, int[] v, int m) {
        // write your code here
        int n = a.length;
        if (n == 0) {
            return 0;
        }

        int [][] f = new int [n + 1][m + 1];
        f[0][0] = 0;
        for (int i = 1; i <= m; i++) {
            f[0][i] = -1;
        }

        for (int i = 1; i <=n; i++) {
            for (int j = 0; j<= m; j++) {
                f[i][j] = f[i - 1][j];
                if (j >= a[i - 1] && f[i][j - a[i - 1]] != -1) {
                    f[i][j] = Math.max(f[i][j], f[i][j - a[i - 1]] + v[i - 1]);
                }
            }
        }

        int res = 0;
        for (int i = 0; i <= m; i++) {
            if (f[n][i] != -1) {
                res = Math.max(res, f[n][i]);
            }
        }

        return res;
    }
}

3.2.2 C++实现的O(MN)算法复杂度

class Solution {
public:
    /**
     * @param a: an integer array
     * @param v: an integer array
     * @param m: An integer
     * @return: an array
     */
    int backPackIII(vector<int> &a, vector<int> &v, int m) {
        // write your code here
        int n = a.size();
        if (n <= 0) {
            return 0;
        }

        vector<vector<int>> f(n + 1, vector<int>(m + 1, -1));
        f[0][0] = 0;

        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                if (j >= a[i - 1] && f[i][j - a[i - 1]] != -1) {
                    f[i][j] = max(f[i][j], f[i][j - a[i - 1]] + v[i - 1]);
                }
            }
        }

        int res = 0;
        for (int i = 0; i <= m; i++) {
            if (f[n][i] != -1) {
                res = max(res, f[n][i]);
            }
        }

        return res;
    }
};

3.2.3 空间复杂度优化为O(m)

class Solution {
public:
    /**
     * @param a: an integer array
     * @param v: an integer array
     * @param m: An integer
     * @return: an array
     */
    int backPackIII(vector<int> &a, vector<int> &v, int m) {
        // write your code here
        int n = a.size();
        if (n <= 0) {
            return 0;
        }

        vector<int> f(m + 1, -1);
        f[0] = 0;

        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= m; j++) {
                if (j >= a[i - 1] && f[j - a[i - 1]] != -1) {
                    f[j] = max(f[j], f[j - a[i - 1]] + v[i - 1]);
                }
            }
        }

        int res = 0;
        for (int i = 0; i <= m; i++) {
            if (f[i] != -1) {
                res = max(res, f[i]);
            }
        }

        return res;
    }
};