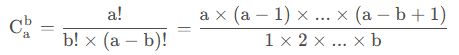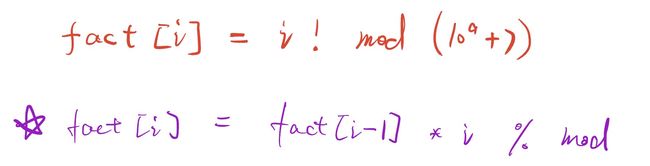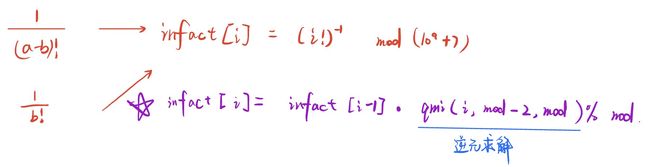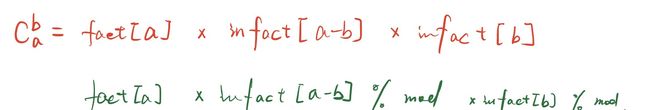三十六、数学知识——组合数(递推法 + 预处理法 + 卢卡斯定理 + 分解质因数求解组合数 + 卡特兰数)
组合数算法主要内容
- 一、基本思路
-
- 1、组合数基本概念
- 2、递推法——询问次数多 + a b 值较小 + 模处理(%mod)
- 3、预处理阶乘方法——询问次数较多 + a b 值很大 + 模处理(%mod)
- 4、卢卡斯定理——询问次数较少 + (a b 值很大) + mod模也很大
- 5、分解质因数法(无模直接求解)——没有模运算 + 大数运算求解
- 6、卡特兰数——多问题可转化为此问题 + 组合数求解
- 二、Java、C语言模板实现
- 三、例题题解
一、基本思路
1、组合数基本概念
2、递推法——询问次数多 + a b 值较小 + 模处理(%mod)
- 使用条件:
-
- 1 - 10万组询问
-
- 1 ≤ b ≤ a ≤ 2000
- 公式如下:
- 如何理解:
-
-
- 在进行选择的时候,包含需要的的一个(已选一个) C b − 1 a − 1 C\begin{matrix} b-1 \\ a-1 \end{matrix} Cb−1a−1
-
-
-
- 在进行选择的时候,不包含需要选的那个(1个未选) C b a − 1 C\begin{matrix} b \\ a-1\end{matrix} Cba−1
-
-
- 两种情况相加即为递推公式,即为所需内容。
3、预处理阶乘方法——询问次数较多 + a b 值很大 + 模处理(%mod)
- 条件:
-
- 1万次问询
-
- 1 ≤ b ≤ a ≤ 10^5
- 公式:
- 分部求解:
-
- a!阶乘求解 :
-
- 注意此处如果 mod 是质数则可以使用快速幂进行逆元求解,不是质数则需要使用扩展欧几里得算法进行逆元求解。
-
- 组合求解:
- 总结:
4、卢卡斯定理——询问次数较少 + (a b 值很大) + mod模也很大
- 条件:
-
- 20次询问;
-
- 1 ≤ b ≤ a ≤ 10^18
-
- 1 ≤ p ≤ 10^5
- 定理:
- 推导过程:(说实话没看懂,感觉可以直接背过模板进行计算)
5、分解质因数法(无模直接求解)——没有模运算 + 大数运算求解
-
步骤:
-
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
- 筛法求出范围内的所有质数
- 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + …
- 用高精度乘法将所有质因子相乘
-
注意:说实话没怎么看懂,我还是背模板吧
6、卡特兰数——多问题可转化为此问题 + 组合数求解
- 卡特兰数简介:
- 卡特兰数是组合数学中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图和比利时的数学家欧仁·查理·卡特兰的名字来命名,其前几项为(从第0项开始):1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
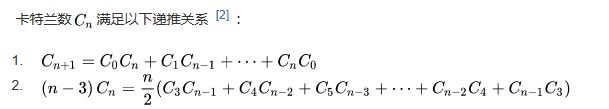
- 卡特兰数结论:
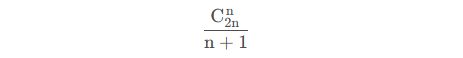
- 卡特兰数推导(来自csdn作者:你好世界wxx):
-
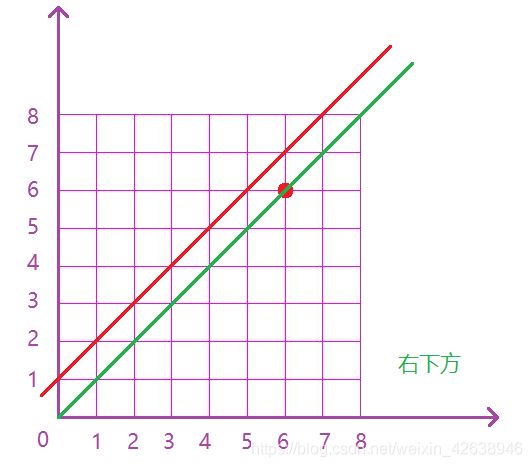
- 首先我们需要将上述问题转换成一个等价的问题:在一个二维平面内,从(0, 0)出发到达(n, n),每次可以向上或者向右走一格,0代表向右走一个,1代表向上走一格,则每条路径都会代表一个01序列,则满足任意前缀中0的个数不少于1个数序列对应的路径则右下侧,如下图:
-
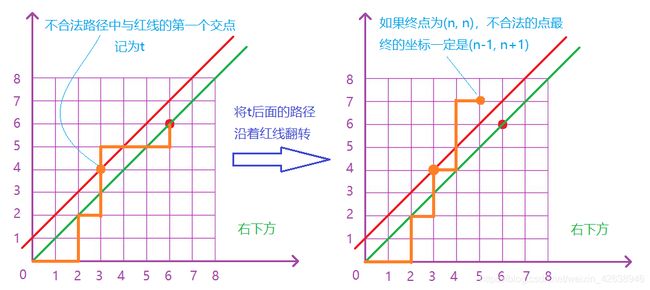
- 符合要求的路径必须严格在上图中红色线的下面(不可以碰到图中的红线,可以碰到绿线)。则我们考虑任意一条不合法路径,例如下图:
-
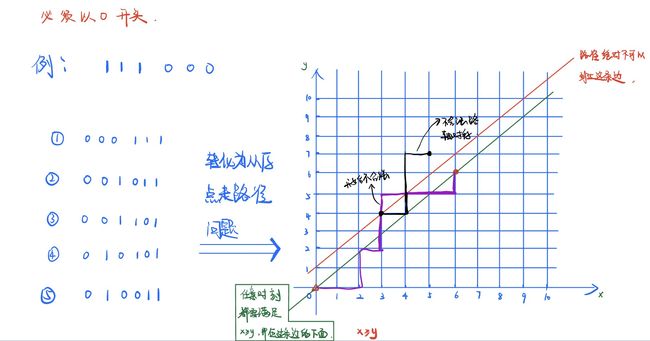
- 补充:
- 举例:
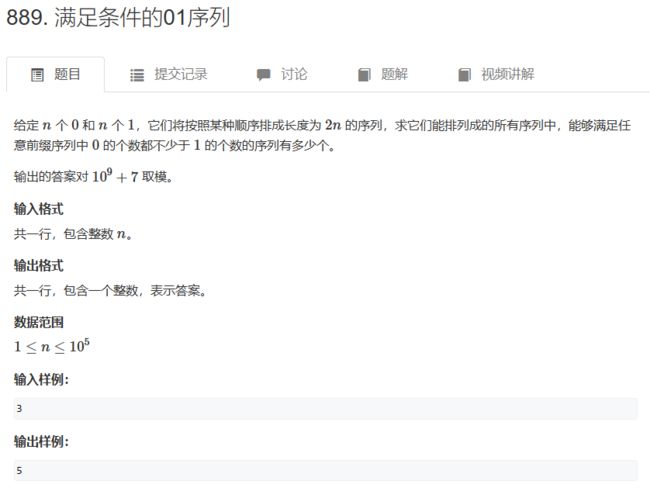
- 给定 n 个 0和 n 个 1,它们将按照某种顺序排成长度为 2n 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 0的个数都不少于 1 的个数的序列有多少个。输出的答案对 10^9+7取模。
- 注意:
-
- mod为质数进行逆元求解:快速幂
-
- mod非质数求解逆元:扩展欧几里得算法
二、Java、C语言模板实现
- 递推法:
// java 模板
static long[][] c = new long[N][N];
static void init(){ // 直接进行预处理,不用每次进行产生,就会减小时间复杂度
for(int i = 0; i < N; i++){
for(int j = 0; j <= i; j++){
if(j == 0){
c[i][j] = 1;
}else{
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % Mod; // c[i][j]实际上i是底数,j是选取的数,即 i = a, j = b;
}
}
}
}
- 预处理方法:
// java 模板
static int mod = (int)(1e9 + 7);
static long[] fact = new long[N]; // 使用 long 是为了防止爆 int
static long[] infact = new long[N];
static long qmi(long a, long k, long p){ // 快速幂求解逆元,其中k = mod - 2 使用费马定理求解逆元
long res = 1;
while((k != 0)){
if((k & 1) == 1){
res = res * a % p;
}
k >>= 1;
a = a * a % p;
}
return res;
}
static void init(){ // 对fact[] infact[] 两个数组进行预处理,后面只需要简单计算即可以求出
fact[0] = 1;
infact[0] = 1;
for(int i = 1; i < N; i++){
fact[i] = fact[i - 1] * i % mod; // a! 阶乘求解
infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod; // 1/(b!) 阶乘倒数求解
}
}
// 组合数求解
long result = (fact[a] * infact[b] % mod) * infact[a - b] % mod;
- 卢卡斯定理:
// java 模板
static long p;
static long qmi(long a, long k){ // 快速幂求解
long res = 1;
while(k != 0){
if((k & 1) == 1){
res = res * a % p;
}
k >>=1;
a = a * a % p;
}
return res;
}
static long C(long a, long b){
// 计算Cab,用的是预处理阶乘的方法————此处后面还会常用,一定要熟记,是进行Cab求解重要方法
long res = 1;
for(long i = 1,j = a; i <= b; i++,j--){
res = res * j % p;
res = res * qmi(i , p - 2)% p; // qmi快速幂进行其中的逆元求解
}
return res;
}
static long lucas(long a, long b){ // 卢卡斯定理求解 Cab
if(a < p && b < p){
return C(a, b); // 不需要进行模处理,直接就可以计算
}
return C(a % p, b % p) * lucas(a/p, b/p) % p; // 卢卡斯公式
}
- 分解质因数法(无模直接求解):
// java 模板
static int[] sum = new int[N];
static int[] primes = new int[N];
static boolean[] st = new boolean[N];
static int cnt;
//线性筛筛质数
static void get_primes(int x){
for(int i=2; i<=x; i++){
if(!st[i]) primes[cnt++] = i;
for(int j=0; primes[j]<=x/i; j++){
st[primes[j]*i] = true;
if(i%primes[j]==0) break;
}
}
}
//获得n!中某个质数的个数
static int get(int n, int p){
int res = 0;
while(n!=0){
res+=n/p;
n/=p;
}
return res;
}
// 主函数
get_primes(a);
for(int i=0; i<cnt; i++){
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a-b, p); // 最终得到质数个数
}
BigInteger res = new BigInteger("1"); // 大数
for(int i=0; i < cnt; i++){ // 质数个数
int p = primes[i];
for(int j=0; j<sum[i]; j++){
res = res.multiply(new BigInteger(String.valueOf(p))); // 阶乘求解
}
}
- 卡特兰数:
// Java模板
static long qmi(long a, long k){ // 快速幂求解质数逆元
long res = 1;
while(k != 0){
if((k & 1) == 1){
res = res * a % mod;
}
k >>= 1;
a = a * a % mod;
}
return res;
}
static long C(long a, long b){
// 此处求解 ab 范围不是很大的————组合数 % mod
// 假如ab范围更大的话,则需要使用卢卡斯定理
long res = 1;
for(long i = 1, j = a; i <= b;i++, j--){
res = res * j % mod;
res = res * qmi(i , mod - 2) % mod;
}
return res;
}
// 主函数
// !!!!!!可以用逆元来表示 (1/(n + 1)!)
long result = C(2 * n, n) * qmi(n + 1, mod - 2) % mod ; // 此处用逆元来表示(1/(n + 1)!)
- 扩展欧几里得算法:
import java.util.*;
public class Main{
static int m = (int) 1e9 + 7;
public static int exgcd(int a,int b,int[] x,int[] y){ // 扩展欧几里得算法
if(b == 0){
x[0] = 1; y[0] = 0;
return a;
}
int d = exgcd(b,a % b,y,x);
y[0] -= (a / b) * x[0] % m;
return d;
}
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
//卡特兰数公式;c[2n][n] - c[2n][n-1] = c[2n][n] / ( n + 1)
int a = 2 * n;
int b = n;
int[] x = new int[1];
int[] y = new int[1];
long res = 1;
for(int i = a ;i > a - b; i --) res = res * i % m;
for(int i = 1 ; i <= n ; i ++ ){
exgcd(i,m,x,y);
res =( res * x[0] % m + m )% m;//同下
}
exgcd(n + 1, m,x,y);
//这里是因为有可能x[0]是系数所以有可能是负数,所以模之后在加上一个m在模,就可以得到正
res = (res * x[0] % m + m) % m;
System.out.println(res);
}
}
- C++模板
// C++ 模板,由yxc实现
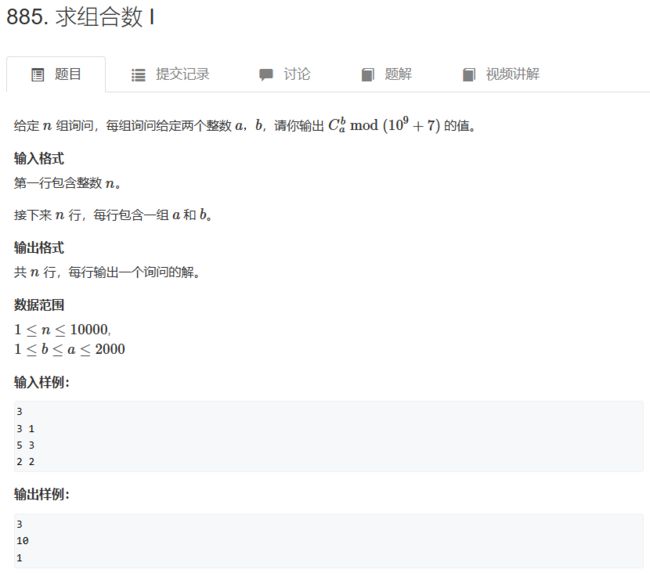
1、递推法求组合数 —— 模板题 AcWing 885. 求组合数 I
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
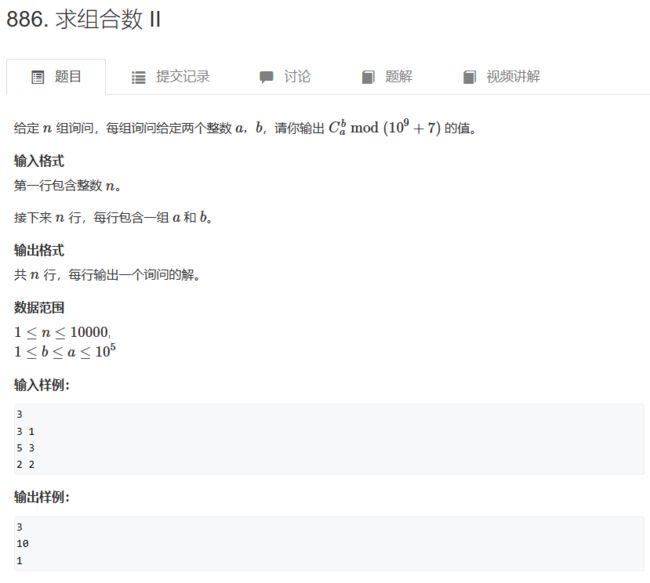
2、通过预处理逆元的方式求组合数 —— 模板题 AcWing 886. 求组合数 II
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
如果取模的数是质数,可以用费马小定理求逆元
int qmi(int a, int k, int p) // 快速幂模板
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
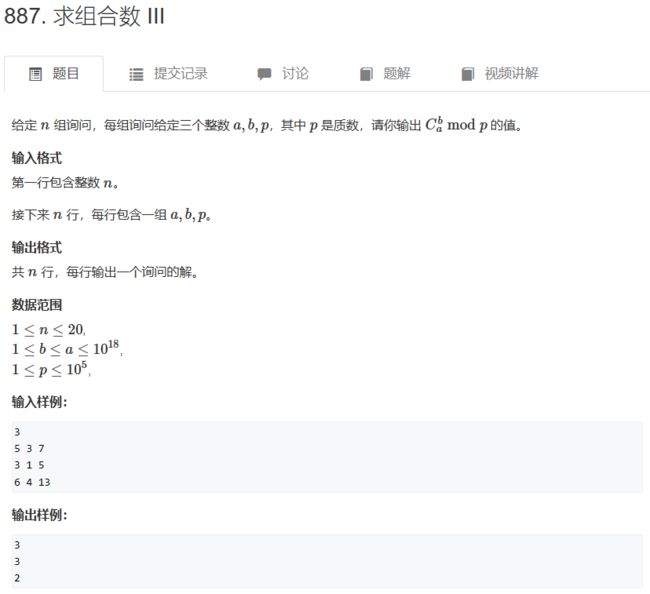
3、Lucas定理 —— 模板题 AcWing 887. 求组合数 III
若p是质数,则对于任意整数 1 <= m <= n,有:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)
int qmi(int a, int k, int p) // 快速幂模板
{
int res = 1 % p;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p) // 通过定理求组合数C(a, b)
{
if (a < b) return 0;
LL x = 1, y = 1; // x是分子,y是分母
for (int i = a, j = 1; j <= b; i --, j ++ )
{
x = (LL)x * i % p;
y = (LL) y * j % p;
}
return x * (LL)qmi(y, p - 2, p) % p;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
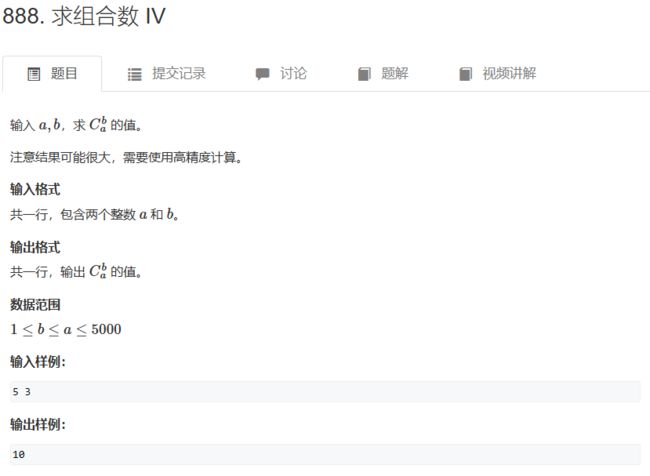
4、分解质因数法求组合数 —— 模板题 AcWing 888. 求组合数 IV
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
3. 用高精度乘法将所有质因子相乘
int primes[N], cnt; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉
void get_primes(int n) // 线性筛法求素数
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p) // 求n!中的次数
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b) // 高精度乘低精度模板
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
get_primes(a); // 预处理范围内的所有质数
for (int i = 0; i < cnt; i ++ ) // 求每个质因数的次数
{
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ ) // 用高精度乘法将所有质因子相乘
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
5、卡特兰数 —— 模板题 AcWing 889. 满足条件的01序列
给定n个0和n个1,它们按照某种顺序排成长度为2n的序列,满足任意前缀中0的个数都不少于1的个数的序列的数量为: Cat(n) = C(2n, n) / (n + 1)
三、例题题解
// java题解实现
// 递推法
import java.util.*;
import java.io.*;
public class Main{
static int Mod = (int)(1e9 + 7); // 此处的高次方值+7要用括号括起来
static int N = 2010;
static long[][] c = new long[N][N];
static void init(){ // 直接进行预处理,不用每次进行产生,就会减小时间复杂度
for(int i = 0; i < N; i++){
for(int j = 0; j <= i; j++){
if(j == 0){
c[i][j] = 1;
}else{
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % Mod; // c[i][j]实际上i是底数,j是选取的数
}
}
}
}
public static void main(String[] args) throws IOException {
init();
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String str1 = in.readLine();
int n = Integer.parseInt(str1);
for(int i = 0; i < n; i++){
String[] str2 = in.readLine().split(" ");
int a = Integer.parseInt(str2[0]);
int b = Integer.parseInt(str2[1]);
System.out.println(c[a][b]);
}
}
}
// 预处理方法求解组合数
import java.util.*;
import java.io.*;
public class Main{
static int N = 100010; // 数据比较大使用此方法
static int mod = (int)(1e9 + 7);
static long[] fact = new long[N]; // 使用 long 是为了防止爆 int
static long[] infact = new long[N];
static long qmi(long a, long k, long p){ // 快速幂求解逆元,其中k = mod - 2 使用费马定理求解逆元
long res = 1;
while((k != 0)){
if((k & 1) == 1){
res = res * a % p;
}
k >>= 1;
a = a * a % p;
}
return res;
}
static void init(){ // 对fact[] infact[] 两个数组进行预处理,后面只需要简单计算即可以求出
fact[0] = 1;
infact[0] = 1;
for(int i = 1; i < N; i++){
fact[i] = fact[i - 1] * i % mod; // a! 阶乘求解
infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod; // 1/(b!) 阶乘倒数求解
}
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String str1 = in.readLine();
int n = Integer.parseInt(str1);
init(); // 预处理阶乘数组
while(n-- != 0){
String[] str2 = in.readLine().split(" ");
int a = Integer.parseInt(str2[0]);
int b = Integer.parseInt(str2[1]);
System.out.println((fact[a] * infact[b] % mod) * infact[a - b] % mod);
// 组合数求解,组合数公式得来
}
}
}
// 卢卡斯定理需要解决的问题:
// 1、问询次数很小
// 2、组合数中的a,b,p范围很大
import java.util.*;
import java.io.*;
public class Main{
static long p;
static long qmi(long a, long k){ // 快速幂求解
long res = 1;
while(k != 0){
if((k & 1) == 1){
res = res * a % p;
}
k >>=1;
a = a * a % p;
}
return res;
}
static long C(long a, long b){ // 计算Cab,用的是预处理阶乘的方法
long res = 1;
for(long i = 1,j = a; i <= b; i++,j--){
res = res * j % p;
res = res * qmi(i , p - 2)% p; // qmi快速幂进行其中的逆元求解
}
return res;
}
static long lucas(long a, long b){ // 卢卡斯定理
if(a < p && b < p){
return C(a, b); // 不需要进行模处理,直接就可以计算
}
return C(a % p, b % p) * lucas(a/p, b/p) % p; // 卢卡斯公式
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String str1 = in.readLine();
int n = Integer.parseInt(str1);
while(n-- != 0){
String[] str2 = in.readLine().split(" ");
long a = Long.parseLong(str2[0]); // 此处是将String转换成long类型
long b = Long.parseLong(str2[1]);
p = Long.parseLong(str2[2]);
System.out.println(lucas(a, b));
}
}
}
// 分解质因数求解
import java.io.*;
import java.math.BigInteger;
import java.util.*;
class Main{
static int N = 100010;
static int[] sum = new int[N];
static int[] primes = new int[N];
static boolean[] st = new boolean[N];
static int cnt;
//线性筛筛质数
static void get_primes(int x){
for(int i=2; i<=x; i++){
if(!st[i]) primes[cnt++] = i;
for(int j=0; primes[j]<=x/i; j++){
st[primes[j]*i] = true;
if(i%primes[j]==0) break;
}
}
}
//获得n!中某个质数的个数
static int get(int n, int p){
int res = 0;
while(n!=0){
res+=n/p;
n/=p;
}
return res;
}
public static void main(String[]args)throws IOException{
BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
String[]arr=in.readLine().split(" ");
int a=Integer.parseInt(arr[0]);
int b=Integer.parseInt(arr[1]);
get_primes(a);
for(int i=0; i<cnt; i++){
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a-b, p); // 最终得到质数个数
}
BigInteger res = new BigInteger("1"); // 大数
for(int i=0; i < cnt; i++){ // 质数个数
int p = primes[i];
for(int j=0; j<sum[i]; j++){
res = res.multiply(new BigInteger(String.valueOf(p))); // 阶乘求解
}
}
System.out.println(res);
}
}
// 卡特兰数求解
import java.util.*;
import java.io.*;
public class Main{
static int mod = (int)(1e9 + 7);
static long qmi(long a, long k){ // 快速幂求解质数逆元
long res = 1;
while(k != 0){
if((k & 1) == 1){
res = res * a % mod;
}
k >>= 1;
a = a * a % mod;
}
return res;
}
static long C(long a, long b){
// 此处求解 ab 范围不是很大的————组合数 % mod
// 假如ab范围更大的话,则需要使用卢卡斯定理
long res = 1;
for(long i = 1, j = a; i <= b;i++, j--){
res = res * j % mod;
res = res * qmi(i , mod - 2) % mod;
}
return res;
}
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(in.readLine());
long result = C(2 * n, n) * qmi(n + 1, mod - 2) % mod ; // 此处用逆元来表示(1/(n + 1))
System.out.println(result);
}
}