Abaqus实现二自由度振动系统模态计算
Abaqus二自由度系统模态计算及理论验证
- 一、理论计算参考[csdn](https://blog.csdn.net/lijil168/article/details/67647924)
-
- 模态参与因子、模态有效质量有点难度,参考资料
-
- 百度文档
- 知乎一
- 知乎二
- 知乎三
- 二、Abaqus仿真计算结果
-
- 一阶模态:
- 二阶模态:
- 三、Abaqus inp文件
- 四、Abaqus模态结果、广义质量、模态参与因子、模态有效质量等及计算验证
-
- Abaqus计算结果:
- python计算结果:
-
- python计算程序:
- Python程序采用的模态有效质量算法的推导
- 五、Abaqus质量及刚度矩阵导出
-
- inp文件更改
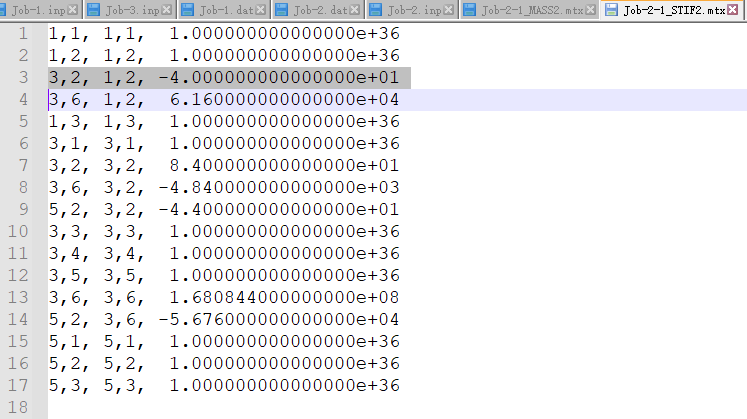
- 质量矩阵
- 刚度矩阵
一、理论计算参考csdn
模态参与因子、模态有效质量有点难度,参考资料
百度文档
知乎一
知乎二
知乎三
二、Abaqus仿真计算结果
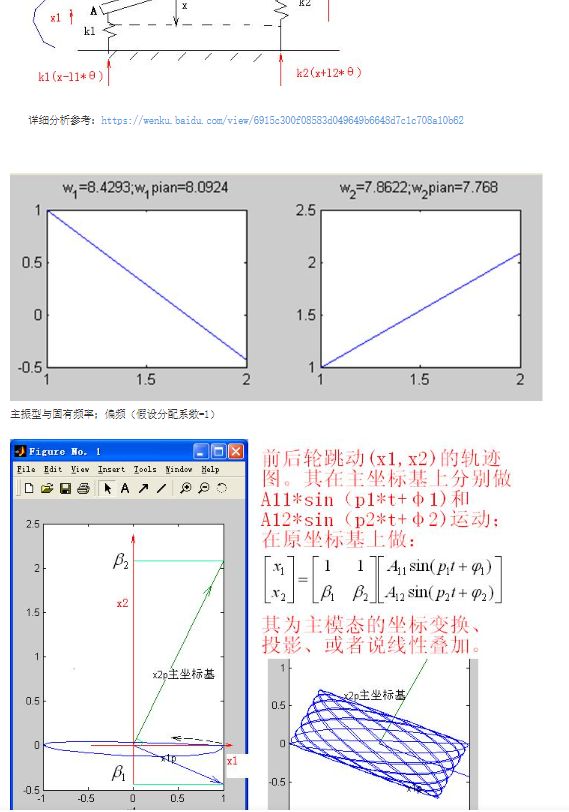
建立刚体动力学模型,不需要网格,只需在interaction建RP点即可,注意车身刚体的3个点采用刚体约束,参考点采用重心。
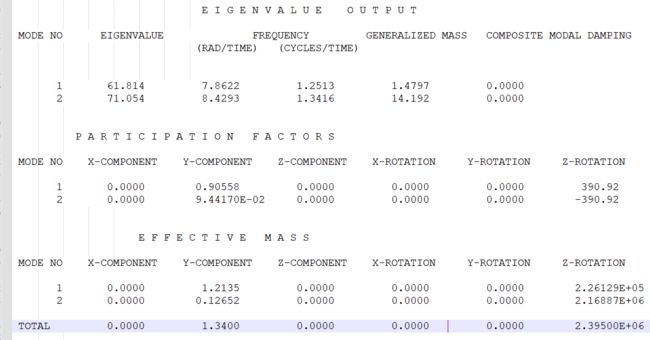
一阶模态:
二阶模态:
三、Abaqus inp文件
*Heading
** Job name: Job-3 Model name: Model-1
** Generated by: Abaqus/CAE 2016
*Preprint, echo=NO, model=NO, history=NO, contact=NO
**
** PARTS
**
**
** ASSEMBLY
**
*Assembly, name=Assembly
*Node
1, -1540., -500., 0.
*Node
2, -1540., 0., 0.
*Node
3, 0., 0., 0.
*Node
4, 1290., 0., 0.
*Node
5, 1290., -500., 0.
*Nset, nset=Set-F
2,
*Nset, nset=_PickedSet31, internal
3,
*Nset, nset=_PickedSet34, internal
3,
*Nset, nset=_PickedSet35, internal
3,
*Nset, nset=_PickedSet41, internal
1, 5
*Nset, nset=_PickedSet42, internal
2, 4
** Constraint: Constraint-1
*Rigid Body, ref node=_PickedSet31, tie nset=_PickedSet42
*Element, type=MASS, elset=_PickedSet43_Inertia-1_MASS_
1, 3
*Mass, elset=_PickedSet43_Inertia-1_MASS_
1.34,
*Element, type=ROTARYI, elset=_PickedSet43_Inertia-1_ROTI_
2, 3
*Rotary Inertia, elset=_PickedSet43_Inertia-1_ROTI_
1., 1., 2.395e+06, 0., 0., 0.
*Spring, elset=Springs/Dashpots-1-spring
40.
*Element, type=SpringA, elset=Springs/Dashpots-1-spring
3, 2, 1
*Spring, elset=Springs/Dashpots-2-spring
44.
*Element, type=SpringA, elset=Springs/Dashpots-2-spring
4, 4, 5
*End Assembly
**
** BOUNDARY CONDITIONS
**
** Name: BC-1 Type: Symmetry/Antisymmetry/Encastre
*Boundary
_PickedSet41, ENCASTRE
** Name: BC-4 Type: Symmetry/Antisymmetry/Encastre
*Boundary
_PickedSet34, YASYMM
** Name: BC-5 Type: Symmetry/Antisymmetry/Encastre
*Boundary
_PickedSet35, ZSYMM
** ----------------------------------------------------------------
**
** STEP: Step-1
**
*Step, name=Step-1, nlgeom=NO, perturbation
*Frequency, eigensolver=Lanczos, sim=NO, acoustic coupling=on, normalization=displacement
2, , , , ,
**
** BOUNDARY CONDITIONS
**
** Name: BC-3 Type: Displacement/Rotation
*Boundary
**
** OUTPUT REQUESTS
**
*Restart, write, frequency=0
**
** FIELD OUTPUT: F-Output-1
**
*Output, field
*Node Output
CF, RF, U
*End Step
四、Abaqus模态结果、广义质量、模态参与因子、模态有效质量等及计算验证
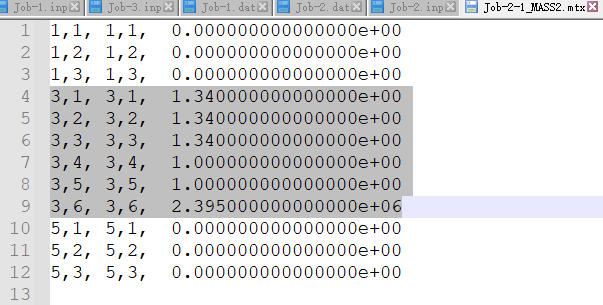
Abaqus计算结果:
python计算结果:
python计算程序:
import numpy as np
import math
#特征值分解法求平等与转动主模态(振型)::
#SH760小轿车空载主要参数
m=1.340 #T
a=1540 #mm
b=1290 #mm
Ic=2395000 #%绕质心的转动惯量
k1=40 #N/mm
k2=44 #N/mm
M_sys=np.array([[m,0],[0,Ic]])
K_sys=np.array([[k1+k2,-(k1*a-k2*b)],[-(k1*a-k2*b),k1*a**2+k2*b**2]])
Value, Vector_Matrix = np.linalg.eig(np.linalg.inv(M_sys)@K_sys)
np.set_printoptions(precision=3, suppress=True)
print('M_sys:\n',M_sys)
print('K_sys:\n',K_sys)
print('wi:\n',np.sqrt(Value))
print('fi:\n',np.sqrt(Value)/2/np.pi)
print('Vector_mode:\n',Vector_Matrix)
#模态质量:
#Abaqus称它为广义质量GENERALIZED MASS!!!
M_mode=Vector_Matrix.T@M_sys@Vector_Matrix
print('M_mode:\n',Vector_Matrix.T@M_sys@Vector_Matrix)
#???当系统在物理坐标系下,施加位移为1的单位激励时,在模态坐标系下的坐标(模态参与因子)为模态向量的逆:
#P A R T I C I P A T I O N F A C T O R S
phi_inv_paticipation_factors=np.linalg.inv(Vector_Matrix)
print('phi_inv_paticipation_factors:\n',phi_inv_paticipation_factors)
#系统各阶模态有效质量为phi_inv_paticipation_factors.T@M_mode@phi_inv_paticipation_factors:
#E F F E C T I V E M A S S
#当模态质量归一化后,模态有效质量就是模态参与因子的平方
#模态质量按列排:
M_effective_mass_i=phi_inv_paticipation_factors**2
for i in range((M_mode.shape)[0]):
M_effective_mass_i[i]*=M_mode[i,i]
print('M_effective_mass_i:\n',M_effective_mass_i)
Python程序采用的模态有效质量算法的推导
五、Abaqus质量及刚度矩阵导出
inp文件更改
*Step,NAME=MATRIX
*MATRIX Generate,STIFFNESS,MASS
*MATRIX OUTPUT,STIFFNESS,MASS
*END STEP