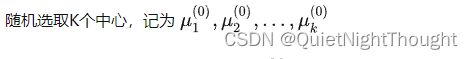机器学习之聚类算法一
文章目录
- 一、简述
-
- 1. 有监督和无监督的区别,以及应用实例
- 2. 为什么是聚类
- 3. 聚类都有哪些
- 二、k-means
-
- 1.k-means,核心思想是什么
-
- 1. 同一个簇内的样本点相似度较高,这里的相似度高,具体指什么
- 2.问题来了:同一簇之间相似,我们知道计算的是同一簇内的样本点之间距离,那么不同簇之间该计算什么呢?
- 2. k-means的目标函数是什么
- 3. k-means的收敛条件是什么
- 4. 为什么k-means的损失函数是各个样本距离所属簇中心点的误差平方和,但是该算法的收敛条件却是当聚类中心不再发生变化或者变化小于某个阈值时
- 5. k-means 算法的评价标准是什么
-
- 1.什么是轮廓系数
- 6.那么根据损失函数,k-means的算法实现流程
- 三、k-means的k值设定
-
-
- `1.手肘法`(Elbow Method):
- `2.轮廓系数`(Silhouette Coefficient):
- `3.GAP统计量`(Gap Statistic):
- `4.DB指数`(Davies-Bouldin Index):
-
- 四、下一篇根据学习的理论进行实践
一、简述
所谓知其然更要知其所以然,结合者理论来敲代码,就能更清楚一些算法的应用场景,知道将我们的业务数据如何处理。
1. 有监督和无监督的区别,以及应用实例
有监督学习和无监督学习是机器学习中的两种常见学习方式,它们的主要区别在于是否需要有人为标注的数据作为训练样本。
有监督学习:在有监督学习中,我们拥有一组已经标记好的数据集合,也就是说每个数据点都已经被标记了一个对应的类别或者值。这些标记可以看做是数据的答案,模型通过学习这些答案来预测新的未知数据的类别或者值。有监督学习包括分类、回归等任务,常用算法有决策树、支持向量机、神经网络等。
无监督学习:在无监督学习中,我们没有任何对数据进行标记的先验知识,因此无法直接利用标记信息进行学习。相反,无监督学习通过寻找数据之间的内在关系、结构和规律,将数据划分为多个集群或者发现数据的低维表示等。无监督学习包括聚类、降维等任务,常用算法有K-Means、PCA、Autoencoder等。
2. 为什么是聚类
我们平时接触的数据,多以非结构化数据居多,如果都使用有监督去学习那么光数据标注一项工作就让我们望而却步。
聚类是数据挖掘领域中常见的一种方法,它可以帮助我们发现数据中隐藏的、未知的结构和规律,从而得到更好的数据理解和分析结果。
3. 聚类都有哪些
聚类算法是一种无监督学习的方法,常用于数据分析和模式识别领域。常见的聚类算法包括:
K-Means:将数据划分为K个簇,每个簇中的数据点距离其所属簇中心最近。层次聚类:根据距离度量将数据点逐步合并成簇,形成一个树状结构,可以选择不同的截断点得到不同的簇。密度聚类:基于数据点密度来划分簇,对于密度可达的点形成一个簇,并且可以通过密度可达进行噪声点的过滤。均值漂移聚类:通过确定局部密度的高点作为中心,逐步向密度高的区域偏移直至收敛,形成一个簇。DBSCAN聚类:基于密度连接原则将高密度区域归为一类,低密度区域归为另一类,同时可以识别出噪声点。GMM(高斯混合模型):基于概率密度函数建立一个高斯混合模型,通过似然函数训练得到每个簇的参数,从而实现聚类。
其中k-means是最为基础的一个,也是最常用的。因此先从基础学起,基础打扎实。
二、k-means
1.k-means,核心思想是什么
k-means聚类的核心思想是将数据集中的样本划分为k个簇(cluster),使得每个样本点都属于其中一个簇,同一个簇内的样本点相似度较高,不同簇之间相似度较低。
具体而言,k-means算法通过迭代来优化每个簇的聚类中心,即每个簇的质心,使得所有样本到其所属簇的质心的距离最小化,从而达到最优的聚类效果。在算法执行过程中需要给定k的值和初始的质心位置,通常情况下可以随机初始化质心位置进行优化。
1. 同一个簇内的样本点相似度较高,这里的相似度高,具体指什么
同一个簇内的样本点相似度较高,指的是它们在某些特征上的数值或属性比较接近,可以用欧式距离、曼哈顿距离等距离度量方式来计算它们之间的相似度。这种相似度也可以称作样本点的“紧密度”,即同一簇的样本点在空间上应该更加接近,而不同簇之间的距离则应该相对较远。在k-means聚类中,通过优化每个簇的质心来最小化所有样本到其所属簇的质心的距离,从而使得同一个簇内的样本点尽可能地相似,不同簇之间的样本点相似度尽可能低。
2.问题来了:同一簇之间相似,我们知道计算的是同一簇内的样本点之间距离,那么不同簇之间该计算什么呢?
通常采用如下两种方式之一:
- 计算不同簇之间的中心点(如 K-means 算法中的质心),并使用
中心点之间的距离作为簇之间的距离度量。这种方法可以有效地衡量不同簇之间的差异性,并且具有较强的可解释性。 - 直接计算
不同簇之间所有样本点之间的距离或相似度,然后取最小值或平均值作为簇之间的距离度量。这种方法可以更加精确地表达不同簇之间的相似度或差异性,但由于其计算复杂度高,因此运算速度较慢。(不建议采用)
2. k-means的目标函数是什么
上面讨论时候,我们发现距离这个词出现的概率很大,可以说在聚类中,距离计算充斥整个流程,那么,就可以根据距离的极限大小来定义损失函数。
在核心思想中:我们期望
同一簇的样本点在空间上应该更加接近,而不同簇之间的距离则应该相对较远
那么损失函数可以定义为各个样本距离所属簇中心点的误差平方和:
3. k-means的收敛条件是什么
收敛条件通常是指当聚类中心不再发生变化或者变化小于某个阈值时,算法就可以停止迭代了。比如K-means算法中,通常会设定一个最大的迭代次数和一个误差阈值,如果聚类中心的变化小于误差阈值,或者达到了最大迭代次数,就会停止迭代。另外一些聚类算法可能会根据自身的特点采用不同的收敛条件,例如层次聚类算法可能会在某个高度上停止合并子集。
4. 为什么k-means的损失函数是各个样本距离所属簇中心点的误差平方和,但是该算法的收敛条件却是当聚类中心不再发生变化或者变化小于某个阈值时
K-means算法的损失函数是各个样本距离所属簇中心点的误差平方和,因为该函数能够度量聚类结果的质量。通过最小化该函数,可以使得同一簇内的数据点更加相似,不同簇之间的数据点更加不同。但是,该损失函数并不能保证K-means算法能够找到全局最优解,因为它容易收敛到局部最优解。
因此,K-means算法的收敛条件是当聚类中心不再发生变化或者变化小于某个阈值时。这是因为当聚类中心不再发生变化时,说明算法已经达到了一个稳定的状态,此时再进行迭代已经无法获得更好的聚类效果。同时,由于K-means算法迭代次数会受到超参数影响,所以设定收敛条件也能够避免算法过度拟合。
5. k-means 算法的评价标准是什么
k-means 算法的评价指标主要有两种:簇内平方和 (SSE) 和轮廓系数 (Silhouette Coefficient)。
-
簇内平方和(SSE):衡量数据点到其所属聚类中心的距离平方和,即“误差平方和”(Sum of Squared Errors, SSE)。SSE越小,表示簇内数据点越接近于聚类中心,聚类效果越好。但是SSE不适合用来比较不同聚类算法的优劣,因为它的取值受数据集大小和维度影响很大。 -
轮廓系数(Silhouette Coefficient):衡量数据点与其所属簇的相似度,以及与其他簇的区分度。轮廓系数的取值范围在[-1, 1]之间,越接近1表示数据点与自身所属簇越相似,与其他簇差异越大,聚类效果越好。反之,如果轮廓系数越接近-1,则表示数据聚类效果不佳。轮廓系数可以用来比较不同聚类算法的优劣,但是只适用于凸型聚类算法(例如K-Means)。
1.什么是轮廓系数
具体来说,对于一个数据点 i,设它所属的簇为 C(i),则轮廓系数 s(i) 定义如下:
s(i) = (b(i) - a(i)) / max(a(i), b(i))
其中 a(i) 表示数据点 i 与同簇中其他数据点的平均距离,b(i) 表示数据点 i 与最近非同簇数据点的平均距离。
轮廓系数的取值范围为 [-1, 1],其中 -1 表示聚类效果非常差,1 表示聚类效果非常好,0 则表示聚类效果一般。通常情况下,轮廓系数越接近 1,表示数据点与自身所属簇越相似,与其他簇差异越大,聚类效果越好。
例如:
 上图我们按照评估指标看一下,以蓝色样本为例,
上图我们按照评估指标看一下,以蓝色样本为例,
1、计算蓝1到自身类别的点距离的平均值记为a(i)
2、计算蓝1分别到紅色类别,绿色类别所有点的距离,求出平均值,取其中最下的值记为b(i)
关于轮廓系数的求解,sklearn算法包中有封装好的轮廓系数API,我们可以直接调用:
sklearn.metric.sihouette_score(X,labels)
计算所有样本的平均轮廓系数
X:特征值
labels:被聚类标记的目标值
6.那么根据损失函数,k-means的算法实现流程
我们的目标是:将给定的数据集划分为K的簇(这里的K是我们的超参数),在进行之前还要给出每个簇中心点。
-
进行数据清洗处理:
在使用k-means算法进行聚类之前,需要对数据进行一定的预处理,主要包括以下几个方面:
数据清洗:去除重复数据、异常值和缺失值等。
数据归一化:将不同特征的数据转化为相同的尺度,以避免某些特征对聚类结果的影响过大。常用的方法包括最小-最大规范化、z-score标准化等。
特征选择:将数据集中与聚类任务无关或冗余的特征剔除,以降低计算成本和噪声干扰。
数据采样:当数据集较大时,可以采用随机抽样或分层抽样等方法来减少数据量,以提高计算效率。
数据转换:对特定的数据类型进行转换,如将文本数据转化为数值型数据。
-
定义损失函数
-
对集合中的每一样本点,计算与我们
所有定义的簇中心距离,选取距离最近的一个划为一簇 -
划分完毕后对每一个簇进行簇中心更新,(更新的方法就是对簇内所有样本点的不同维度求取平均值,从而产生新的簇中心)
-
根据新的簇中心持续4.5两步。当新的簇中心与更新前的簇簇中心之间的距离小于
设定误差阈值或者达到一个最大的迭代次数,训练结束
关于这里的计算更新示例:簇中心更新示例计算演示
三、k-means的k值设定
确定聚类中的簇数量K是非常重要的,它直接影响到聚类结果的质量。以下是一些确定K值的最优方法:
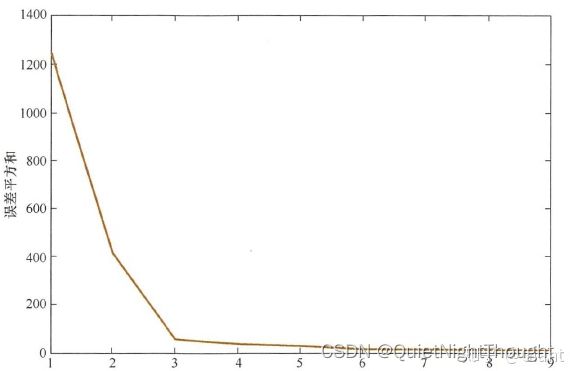
1.手肘法(Elbow Method):
该方法绘制SSE(Sum of Squared Errors)随簇数量增加而变化的图表,在图表上选择一个像手肘弯曲的点作为最佳簇数。
具体实现步骤如下:
簇内平方和 (SSE),具体看评价标准里面
-
从
1开始尝试不同的k值,对于每一个k值,都执行一次k-means算法,得到该k值下的聚类结果。 -
计算
每个样本与其所属簇质心之间的距离平方和(SSE),记为SSE(k)。 -
将SSE(k)的值绘制在坐标轴上,横轴为k值,纵轴为SSE(k)的值,得到一条
随k值递增而递减的曲线。 -
手肘法的核心是:找出曲线中
呈现拐点的位置作为最优的k值。拐点处意味着新增加一个簇时,SSE的下降幅度急剧减小,因此增加更多的簇并不能显著提高聚类效果。 -
通过观察SSE-k曲线,找到
拐点即可确定最优的k值。通常来说,如果SSE-k曲线形状像一个人的手臂,则拐点就是手肘所在的位置,因此称为手肘法。
例如:
尝试不同K值并将对应的损失函数画成折线。手肘法认为图上的拐点就是K的最佳值K=3
2.轮廓系数(Silhouette Coefficient):
该方法评估每个数据点在其所处簇中与邻近簇之间的相似性,并将这些分数平均得到整体轮廓系数。最佳簇数应具有最大平均轮廓系数。
3.GAP统计量(Gap Statistic):
该方法通过比较实际数据和随机生成的数据集之间的区别来确定最佳簇数。
4.DB指数(Davies-Bouldin Index):
该方法度量簇之间的差异性,最佳簇数应具有最小DB指数。
四、下一篇根据学习的理论进行实践
参考文章:
致谢:
[1].https://zhuanlan.zhihu.com/p/184686598
[2].https://zhuanlan.zhihu.com/p/432230028
[3].https://www.jianshu.com/p/b268d7f3fbb9
[4].https://zhuanlan.zhihu.com/p/357072839