高级算法设计——网络流问题
文章目录
- 网络流问题HDU3549
-
- EK算法求解
- 最大流HDU1532
-
- 法一、EK算法求解
- 法二、Dinic算法求解
-
- 如果喜欢我的文章,请记得三连哦,点赞关注收藏,你的每一个赞每一份关注每一次收藏都将是我前进路上的无限动力 !!!↖(▔▽▔)↗感谢支持,下期更精彩!!!
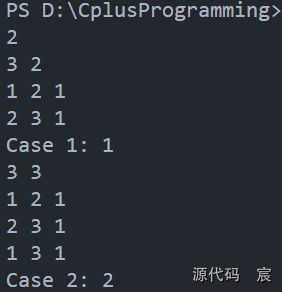
网络流问题HDU3549
EK算法求解
详细C++代码如下:
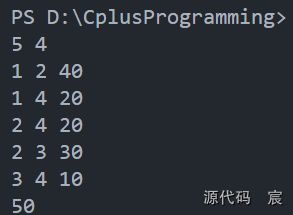
#include最大流HDU1532
法一、EK算法求解
详细C++代码如下:
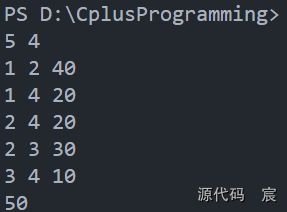
#include法二、Dinic算法求解
详细C++代码如下:
#include