【LeetCode每日一题】【单调栈】2022-10-28 907. 子数组的最小值之和 Java实现

---

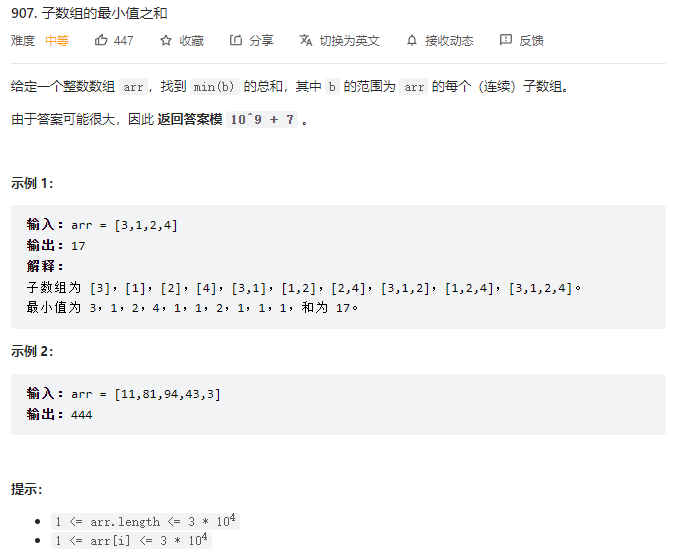
题目链接

https://leetcode.cn/problems/sum-of-subarray-minimums/

题目

我的思路

每个子数组如果只有一个数字，那么，该子数组的最小值就是它本身

如果长度大于一，则需要将这个子数组进行拆分，然后算出最小值

用一个二维数组来存储每个子数组的最小值，超出了内存限制

class Solution {
    public int sumSubarrayMins(int[] arr) {
        int n = arr.length;
        int[][] dp = new int[n][];
        for (int i = 0; i < n; i++) {
            dp[i] = new int[i + 1];
            dp[i][i] = arr[i];
        }
        int i, j;
        for (int k = 0; k < n - 1; k++) {
            i = k + 1;
            j = 0;
            while (i < n) {
                dp[i][j] = Math.min(dp[i][i], dp[i - 1][j]);
                i++;
                j++;
            }
        }
        long res = 0;
        for (i = 0; i < n; i++) {
            for (j = 0; j <= i; j++) {
                res += dp[i][j];
            }
        }
        return (int) (res % 1000000007);
    }
}

其他解法

https://leetcode.cn/problems/sum-of-subarray-minimums/solution/xiao-bai-lang-dong-hua-xiang-jie-bao-zhe-489q/

方案一 暴力（超出时间限制）

class Solution {
    public int sumSubarrayMins(int[] arr) {
        long res = 0;
        int n = arr.length;
        int tmp;
        for (int i = 0; i < n; i++) {
            tmp = arr[i];
            for (int j = i; j < n; j++) {
                tmp = Math.min(tmp, arr[j]);
                res += tmp;
            }
        }
        return (int) (res % 1000000007);
    }
}

时间复杂度：$O(n^2)$

空间复杂度：$O(1)$

方案二 方案一的改进，单调栈+贡献值

根据上面的$O(n^2)$暴力解法，需要去优化时间复杂度

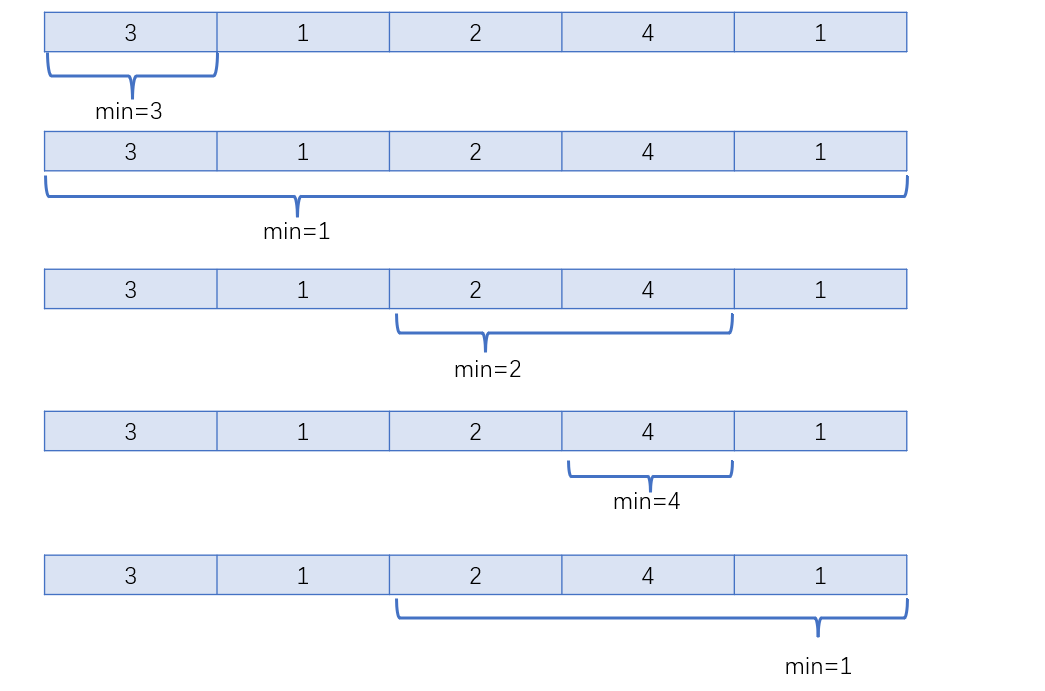
最小值是在一段连续数字中被筛选出来的，也就是说每个最小值都有一定的辐射范围。假设给定数组A=[3,1,2,4,1]，在一段连续数字3、1、2、4、1中，只要其中一段数字包含1，那么这段数字的最小值肯定是1，例如[3,1,2,4,1]，[3,1,2,4]，[3,1,2]，[3,1]等的最小值都为1，把这叫做元素1的辐射范围

从图中可以看出：
下标0的元素3辐射范围为[3]
下标1的元素1辐射范围为[3,1,2,4,1]
下标2的元素2的辐射范围是[2,4]
下标3的元素4的辐射范围是[4]
下标4的元素1辐射范围是[2,4,1]

每个元素E=A[i]的辐射范围都是一个连续数组，这个辐射范围内产生的所有子数组最小值都是E，因此E在每个子数组中对答案的贡献值都为E，如果这个辐射范围内的子数组有n个，那么总贡献值就是n*E。

那么辐射范围内能产生多少个子数组呢？

需要枚举一下能产生多少个不同的左右边界对即可。假设辐射的左边界为left，右边界为right，元素E的下标为i，那么子数组的左边界应该在[left,i]中选取，子数组的有边界应该在[i,right]中选取。因此子数组个数为(i-left+1)*(right-i+1)。

那么我们只需要计算出每个元素的贡献值，然后求和就好了。目前，我们已经知道了i和A[i]，也就是知道了下标和下标对应的值，只需要确定辐射范围，也就是确定left和right

如何求辐射范围

元素E是这个辐射范围的最小值，那么当从元素E的下标i向外扩展时，如果发现某个元素比E大，那么必定属于E的辐射范围，而如果某个元素比E小，那么肯定不属于这个辐射范围，因为E是最小值，整个范围内不应该有比E更小的数

因此，只要我们向左找到第一个比元素A[i]小的数A[left]，向右找到第一个比A[i]小的数A[right]，就可以确定E的辐射范围A[left+1:right)。这就叫做下一个更小/更大的数问题。解决这类问题的通用解法即为单调栈。

注意：
这里说的A[i]和E是一样的含义

具体求解思路

1. 利用单调栈向左找到第一个小于等于 A[i]的数A[left]，遍历顺序为 0到n-1，也就是E的辐射范围的左边界

   • 注意：第一个、小于等于

2. 利用单调栈向右找到第一个小于 A[i]的数A[right]，遍历顺序为 n-1到0，也就是E辐射范围的右边界

   • 注意：第一个、小于

3. 将每个元素的贡献值求和得到最终答案

import java.util.Stack;

class Solution {
    public int sumSubarrayMins(int[] arr) {
        int n = arr.length;

        //每个元素辐射范围的左边界
        int[] left = new int[n];

        //每个元素辐射范围的右边界
        int[] right = new int[n];

        Stack<Integer> stack = new Stack<>();

        //第一次循环先找到所有元素的左边界
        for (int i = 0; i < n; i++) {

            //向左找第一个小于等于E的元素
            while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
                stack.pop();
            }

            if (stack.isEmpty()) {
                left[i] = -1;
            } else {
                left[i] = stack.peek();
            }

            stack.push(i);
        }

        stack.clear();
        //第二次循环找到所有元素的右边界
        for (int i = n - 1; i >= 0; i--) {

            //找到第一个小于E的元素
            while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
                stack.pop();
            }

            if (stack.isEmpty()) {
                right[i] = n;
            } else {
                right[i] = stack.peek();
            }
            stack.push(i);
        }

        //按照贡献度计算即可
        //注意次数left[i]和right[i]实际上记录的是左边界-1和右边界+1，和思路中提到的有一点差别，不用单独+1了
        long res = 0;
        for (int i = 0; i < n; i++) {
            res = (res + ((long) (i - left[i]) * (right[i] - i) * arr[i])) % 1000000007;
        }
        
        return (int) res;
    }
}

注意：再计算左边界或者右边界时，将一侧设置为求解小于等于E的元素，目的是为了解决当一个子数组中有两个最小元素时（[3,1,2,4,1]有两个1），不重复且不遗漏地统计每一个子数组

方案三 方案二改进

上面的代码逻辑清晰，但是经历了两次遍历且用到了额外的空间，可以考虑更简洁的一次遍历直接求出所有元素的左边界和右边界，并且不用额外空间

方案三是方案二的逆向思维，方案二中，每个大于当前元素A[i]的元素出栈以向左求解得到第一个小于A[i]的元素，那么反过来，针对每个出栈的元素，当前元素A[i]就是向右比它更小的第一个元素。这就找到的右边界

每个大于当前元素A[i]的元素都会依次出栈，那么每个入栈元素的栈内相邻的下一个元素就是向左比它更小的第一个元素。这就得到了左边界。

既然左右边界都可以在一次遍历中得到，那么自然可以一次遍历得到贡献值，且不需要额外空间

import java.util.Stack;

class Solution {

    private int getCount(int[] arr, int n, int i) {
        if (i == -1 || i == n) {
            return Integer.MIN_VALUE;
        }
        return arr[i];
    }

    public int sumSubarrayMins(int[] arr) {

        int n = arr.length;

        Stack<Integer> stack = new Stack<>();

        long res = 0;

        for (int i = -1; i <= n; i++) {

            while (!stack.isEmpty() && getCount(arr, n, stack.peek()) > getCount(arr, n, i)) {
                //对于弹出来的这个cur，i相当于cur的右边界
                int cur = stack.pop();

                res = (res + (long) (cur - stack.peek()) * (i - cur) * arr[cur]) % 1000000007;

            }
            stack.push(i);
        }
        return (int) res;
    }
}