本篇文章主要与大家分享一下如何使用matlab进行二维和三维空间的位姿描述及坐标系的变换,文章内容处于更新和补充中,(我同时安装了机器人工具箱9.10版本和10.4版本,因此文章也介绍了两种版本工具箱下的用法)
一、
1、二维空间的位姿描述
(1)在二维空间下对进行坐标系的平移和旋转可以使用se2函数(在9.10版本工具箱中用se2函数,10.4版本为SE2函数),我们在matlab的命令行窗口输入help se2可以查看matlab的帮助文档中对se2函数使用的解释,其参数X,Y分别是在X、Y方向平移的距离,参数THETA是旋转的角度,具体的例子如下:

①在X方向平移1,在Y方向平移2 ,旋转90度
%9.10版本机器人工具箱
T=se2(1,2,90,'deg') %参数THETA为角度制
T=se2(1,2,pi/2) %参数THETA为弧度制
%10.4版本机器人工具箱
T=SE2(1,2,pi/2) %参数THETA为弧度制
T=SE2(1,2,90,'deg') %参数THETA为角度制
运行结果如下:
T =
0.0000 -1.0000 1.0000
1.0000 0.0000 2.0000
0 0 1.0000
(2)在二维空间下对进行坐标系的旋转可以使用rot2函数(10.4版本工具箱),其参数为旋转的角度,具体的例子如下:
R=rot2(pi)
运行结果如下:
R =
-1.0000 -0.0000
0.0000 -1.0000
(3)求二维平面内,平移、旋转的齐次变换矩阵,可以分别用transl2()函数和trot2()函数,具体的例子如下:
%原点平移至(1,2)
transl2(1,2)
%逆时针旋转30度
trot2(30,'deg')
运行结果如下:
ans =
1 0 1
0 1 2
0 0 1
ans =
0.8660 -0.5000 0
0.5000 0.8660 0
0 0 1.0000
(4)我们可以使用trplot2函数(9.10和10.4版本均可使用)绘制出上面介绍的坐标变换图像,我们在matlab的命令行窗口输入help trplot2可以查看matlab的帮助文档中对trplot2函数使用的解释(本文后面介绍的函数也会适当的截取帮助文档内的内容,后面就不做此说明了 在命令行窗口输入help 后面跟想要查询的名字就可以了)通过帮助文档中列出的Options,可以知道我们可以对很多参数进行设定,具体的例子如下:

①例子1:最简单的例子,按照默认值画出上面介绍的T的图像
trplot2(T)
运行结果如下:
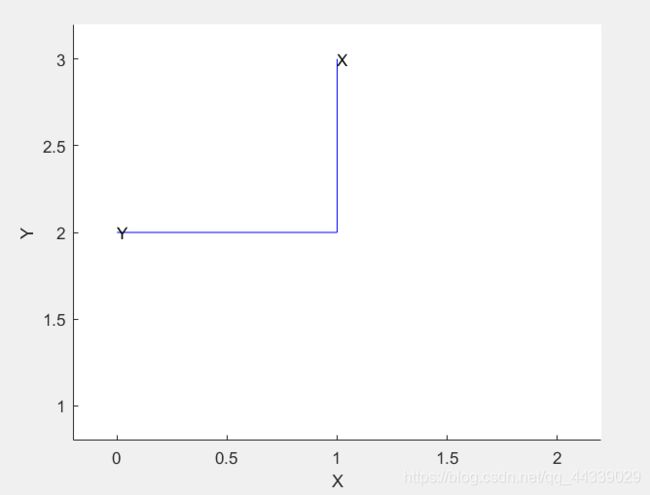
②例子2:画出上面介绍的T的图像,并将新的坐标系命名为A,颜色线条颜色设定为红色
trplot2(T, 'frame', 'A', 'color', 'r')
运行结果如下:
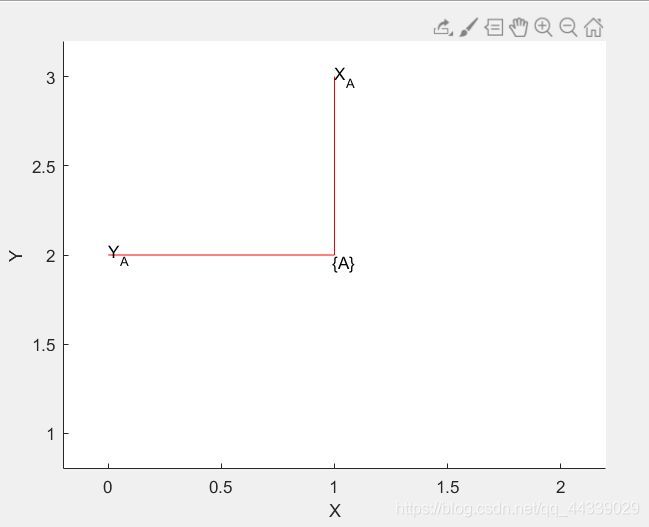
2、三维空间的位姿描述
(1)在三维空间下对进行坐标系的平移可以使用transl函数,其参数X,Y,Z分别是在X、Y、Z方向上平移的距离,具体的例子如下:

①在X方向平移1,在Y方向平移2 ,在Z方向上平移3
T = transl(1, 2, 3)
运行结果如下:
T =
1 0 0 1
0 1 0 2
0 0 1 3
0 0 0 1
(2)在三维空间下对进行坐标系的旋转可以使用rotx、roty、rotz函数,或者trotx、troty、trotz函数,这两类函数的不同之处是rotx、roty、rotz函数是3X3的矩阵,而trotx、troty、trotz函数是4X4的矩阵


①例子1:沿X轴旋转60度(π/3)
T1=rotx(60,'deg') %角度制 3x3
T2=rotx(pi/3) %弧度制 3x3
T3=trotx(pi/3) %弧度制 4x4
运行结果如下:
T1 =
1.0000 0 0
0 0.5000 -0.8660
0 0.8660 0.5000
T2 =
1.0000 0 0
0 0.5000 -0.8660
0 0.8660 0.5000
T3 =
1.0000 0 0 0
0 0.5000 -0.8660 0
0 0.8660 0.5000 0
0 0 0 1.0000
(3)我们可以利用trplot函数绘制出绘制出上面介绍的坐标变换图像,同样我们可以对Options中所列出的参数根据需要进行设定,一些具体的例子如下:



①例子1:绘制出绕X轴旋转60度的图像
T1=rotx(60,'deg') %也可以使用T1=trotx(60,'deg')
trplot(T1)
运行结果如下:
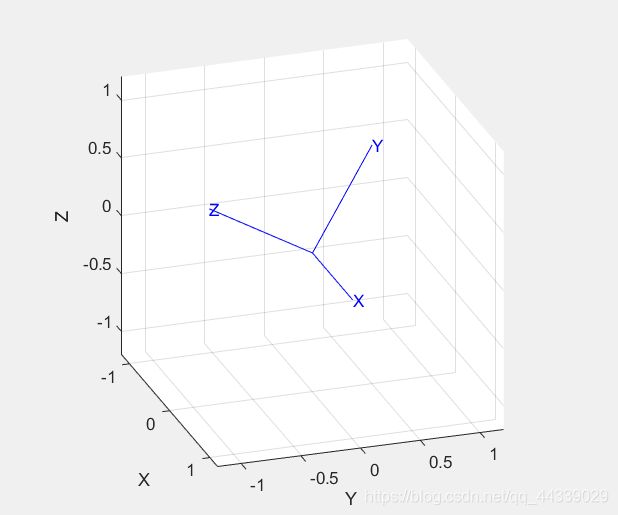
②例子2:绘制出绕X轴旋转60度的图像,并分别以红色、绿色、蓝色显示X、Y、Z轴
T1=rotx(60,'deg') %也可以使用T1=trotx(60,'deg')
trplot(T1,'rgb')
运行结果如下:
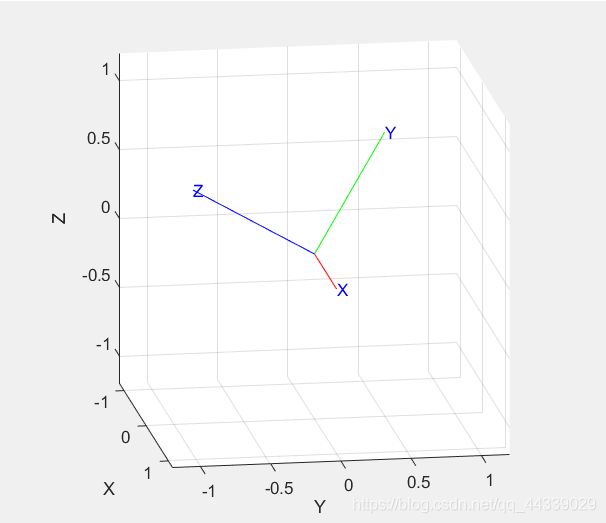
(4)我们可以利用tranimate函数查看动态的变换效果,一些具体的例子如下:

①例子1:绘制出绕X轴旋转60度的动态图像
T1=rotx(60,'deg') %也可以使用T1=trotx(60,'deg')
tranimate(T1)
运行结果如下:
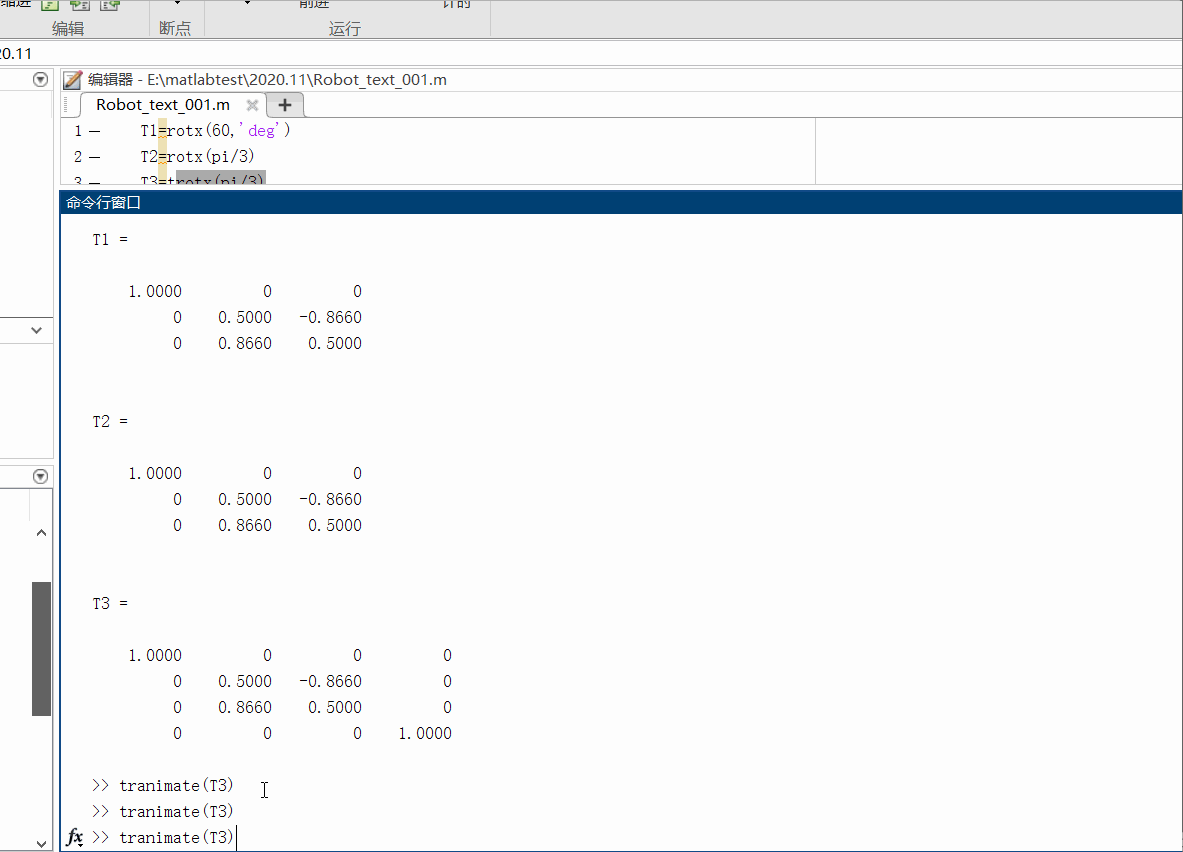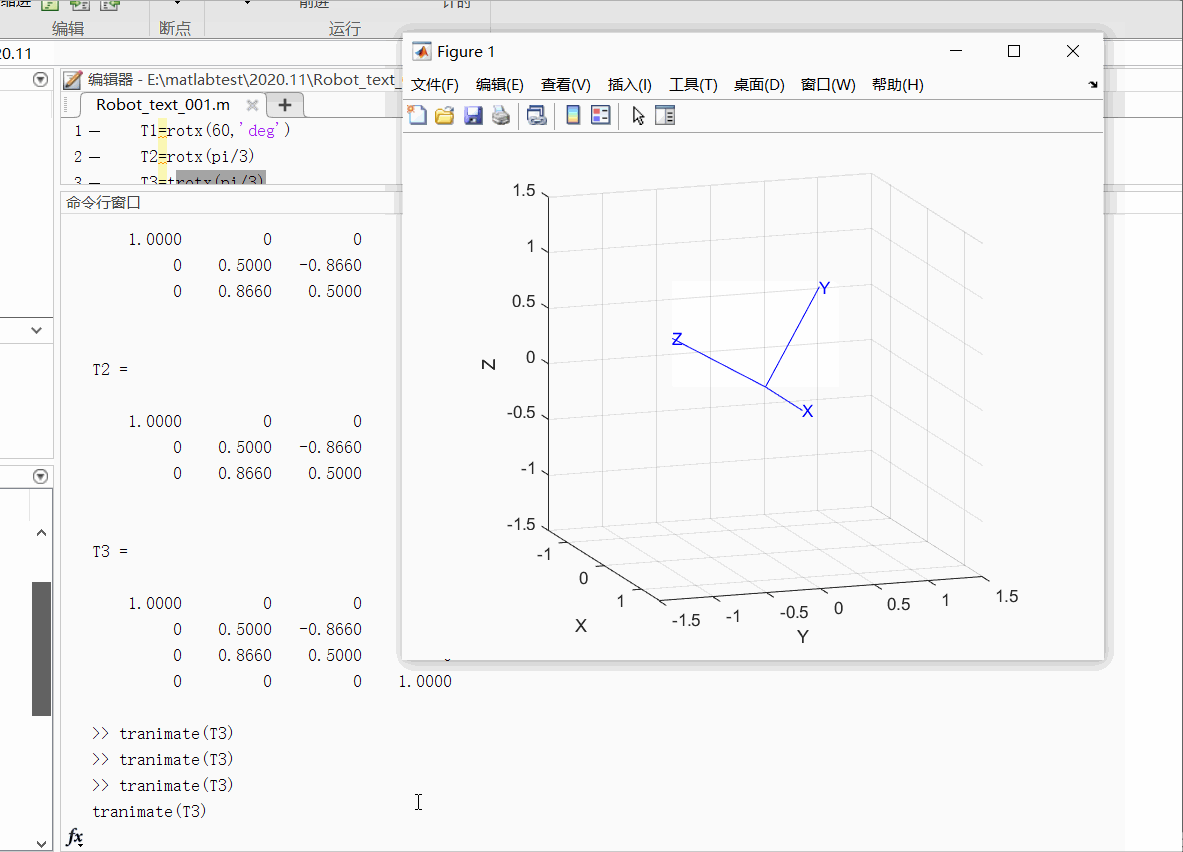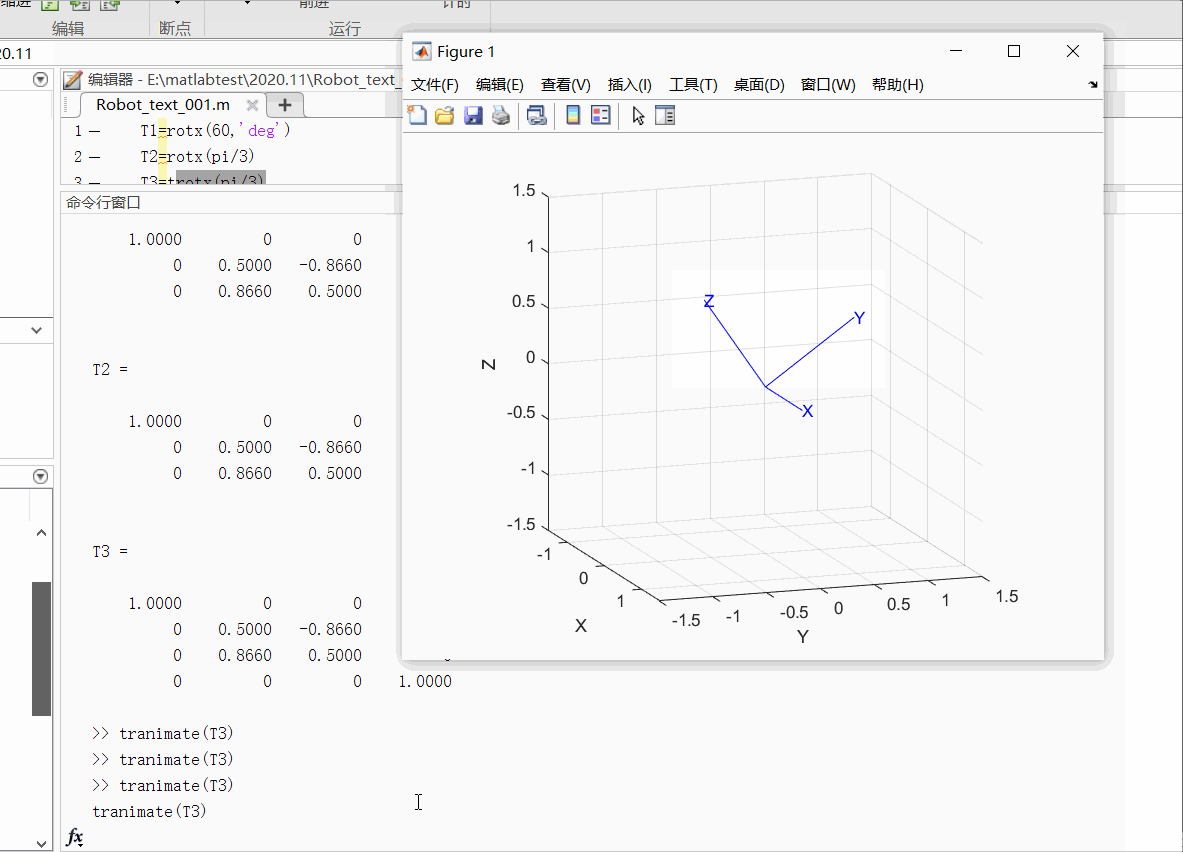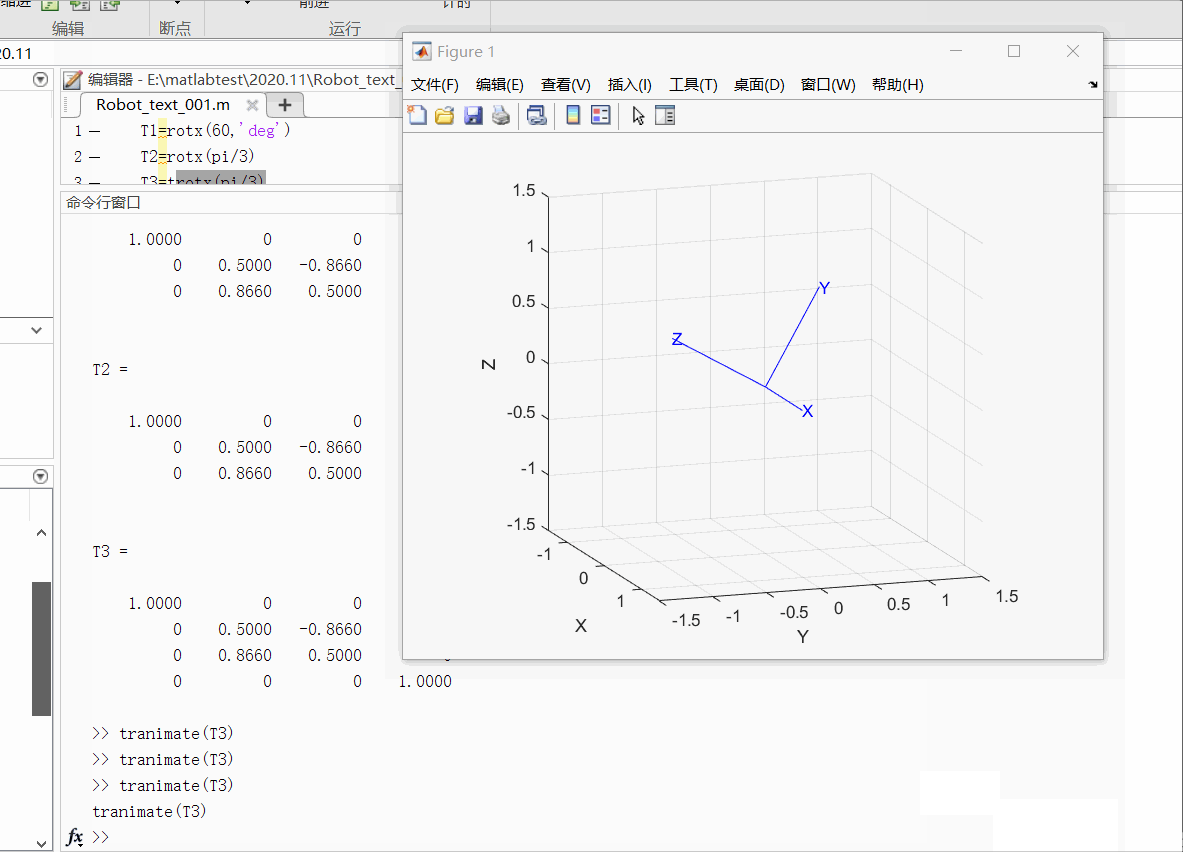
②例子2:绘制出在X方向平移1,在Y方向平移2 ,在Z方向上平移3的动态图像
T4=transl(1,2,3)
tranimate(T4)
运行结果如下:
③例子3:绘制出绕X轴旋转60度的动态图像,并设定每秒要显示的帧数为5(默认为10)
T1=rotx(60,'deg') %也可以使用T1=trotx(60,'deg')
tranimate(T1,'fps','5')
④例子4:绘制出绕X轴旋转60度的动态图像,并将每一帧的图像以图片的形式保存在名为text_001的文件夹中
T1=rotx(60,'deg') %也可以使用T1=trotx(60,'deg')
tranimate(T1,'movie','text_001')
3、将二维空间的位姿矩阵转换成三维空间位姿矩阵
(1)我们可以利用se3函数将二维空间的位姿矩阵转换成三维空间位姿矩阵,具体的例子如下:

T1=se2(1,2,pi/3)
T2=se3(T1)
运行结果如下:
T1 =
0.5000 -0.8660 1.0000
0.8660 0.5000 2.0000
0 0 1.0000
T2 =
0.5000 -0.8660 0 1.0000
0.8660 0.5000 0 2.0000
0 0 1.0000 0
0 0 0 1.0000
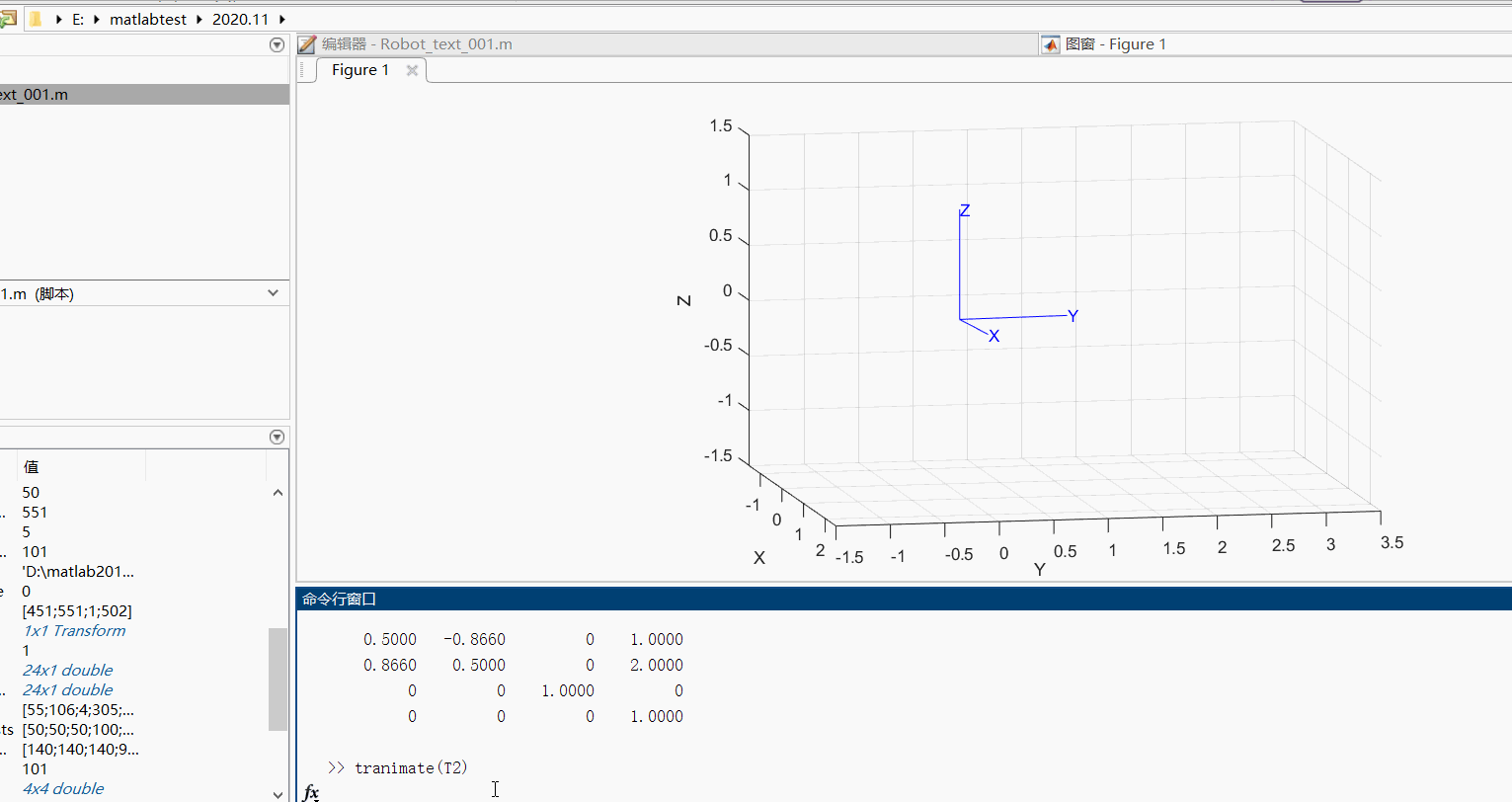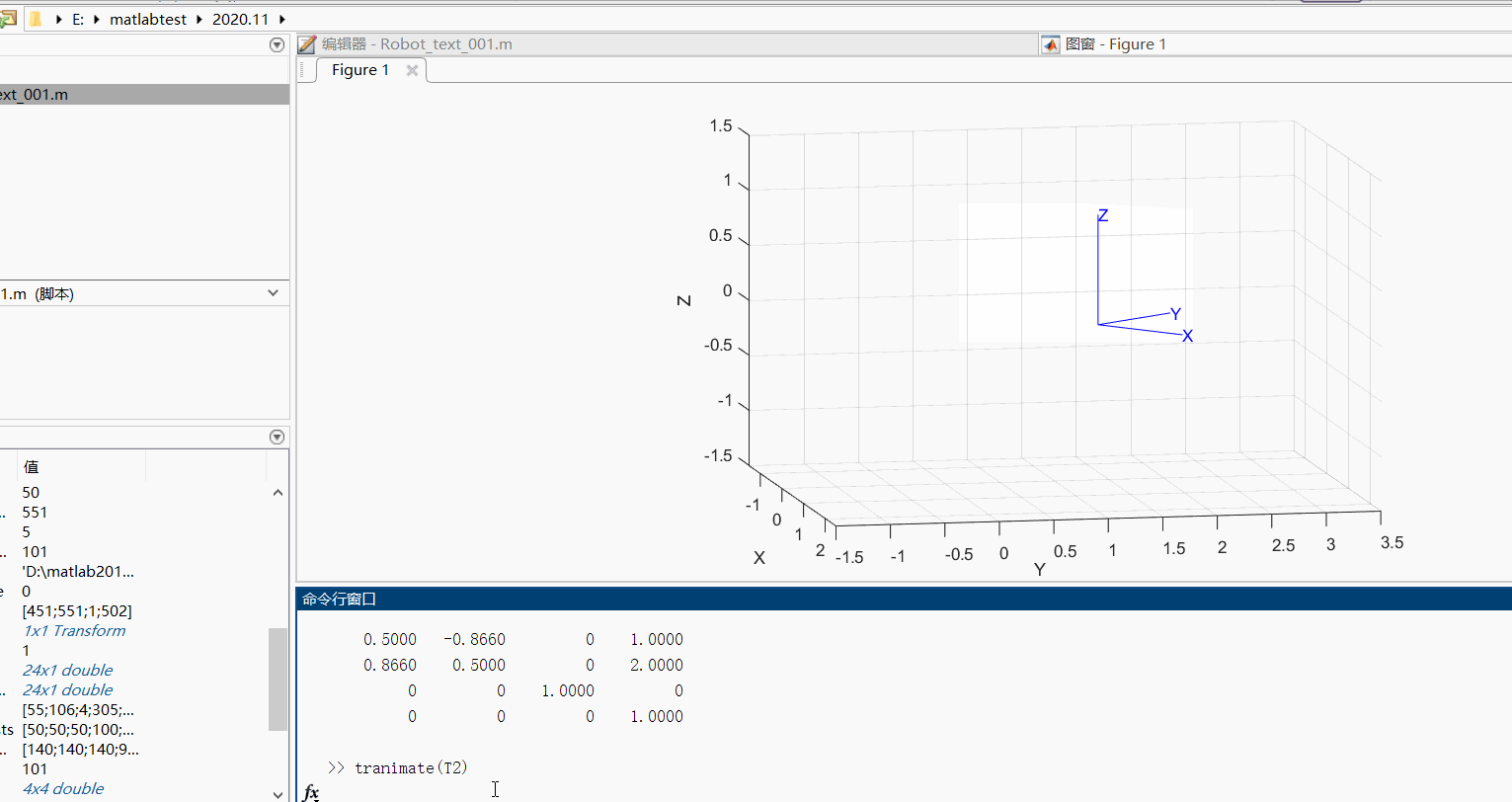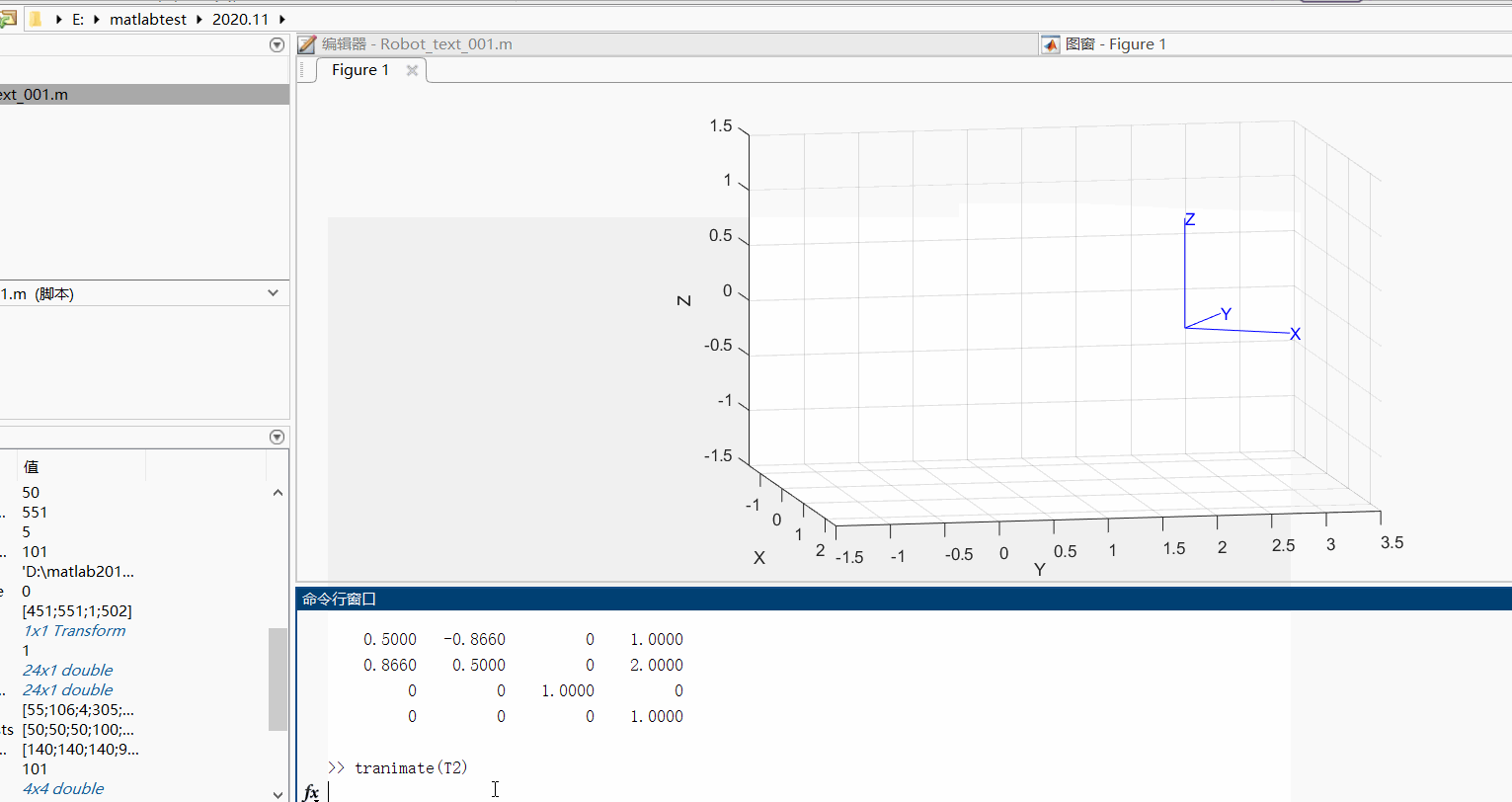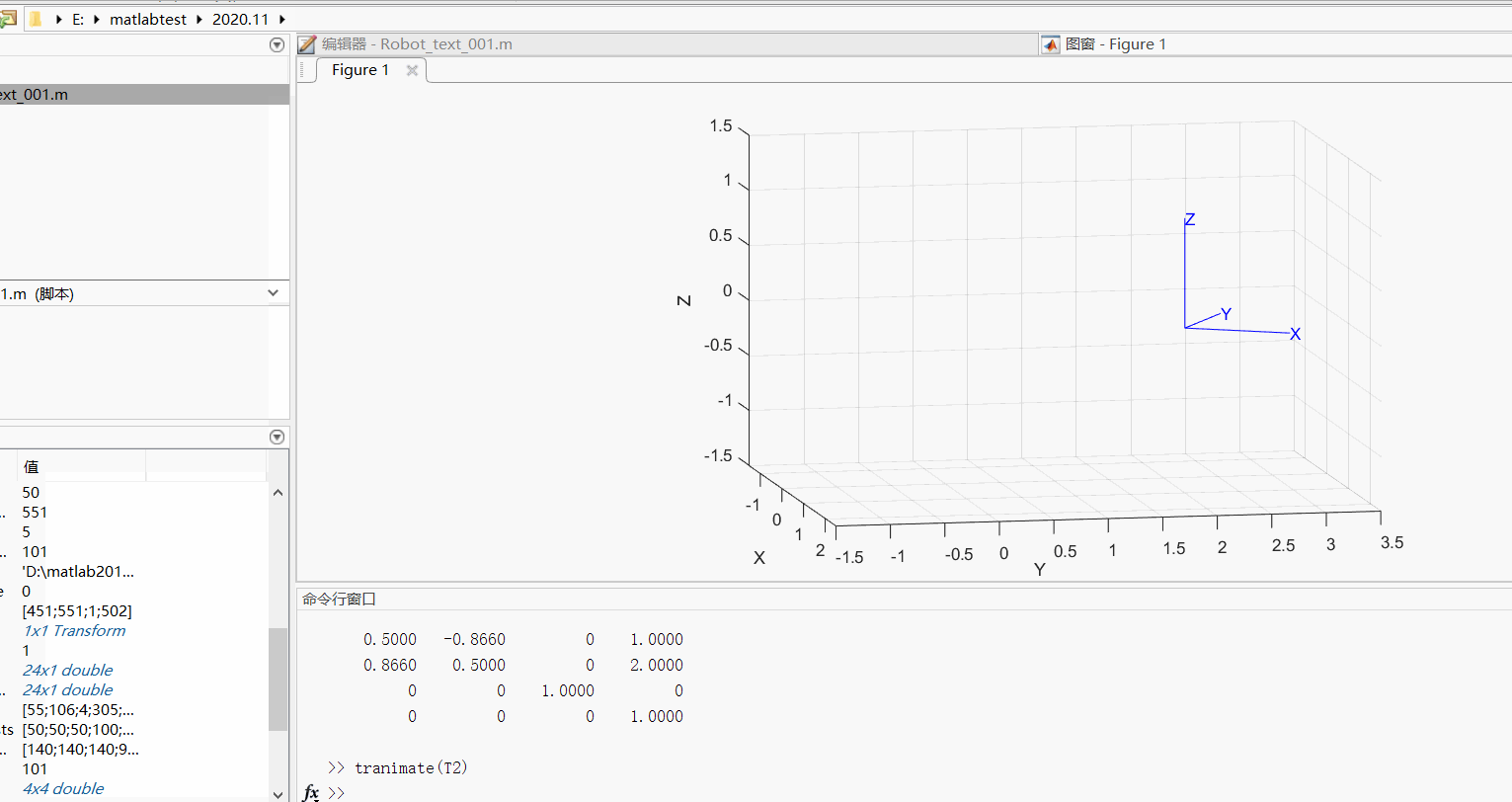
(2)我们可以利用tranimate函数将其动态变换的过程显示出来
T1=se2(1,2,pi/3)
T2=se3(T1)
tranimate(T2)
4、坐标变换的综合实例
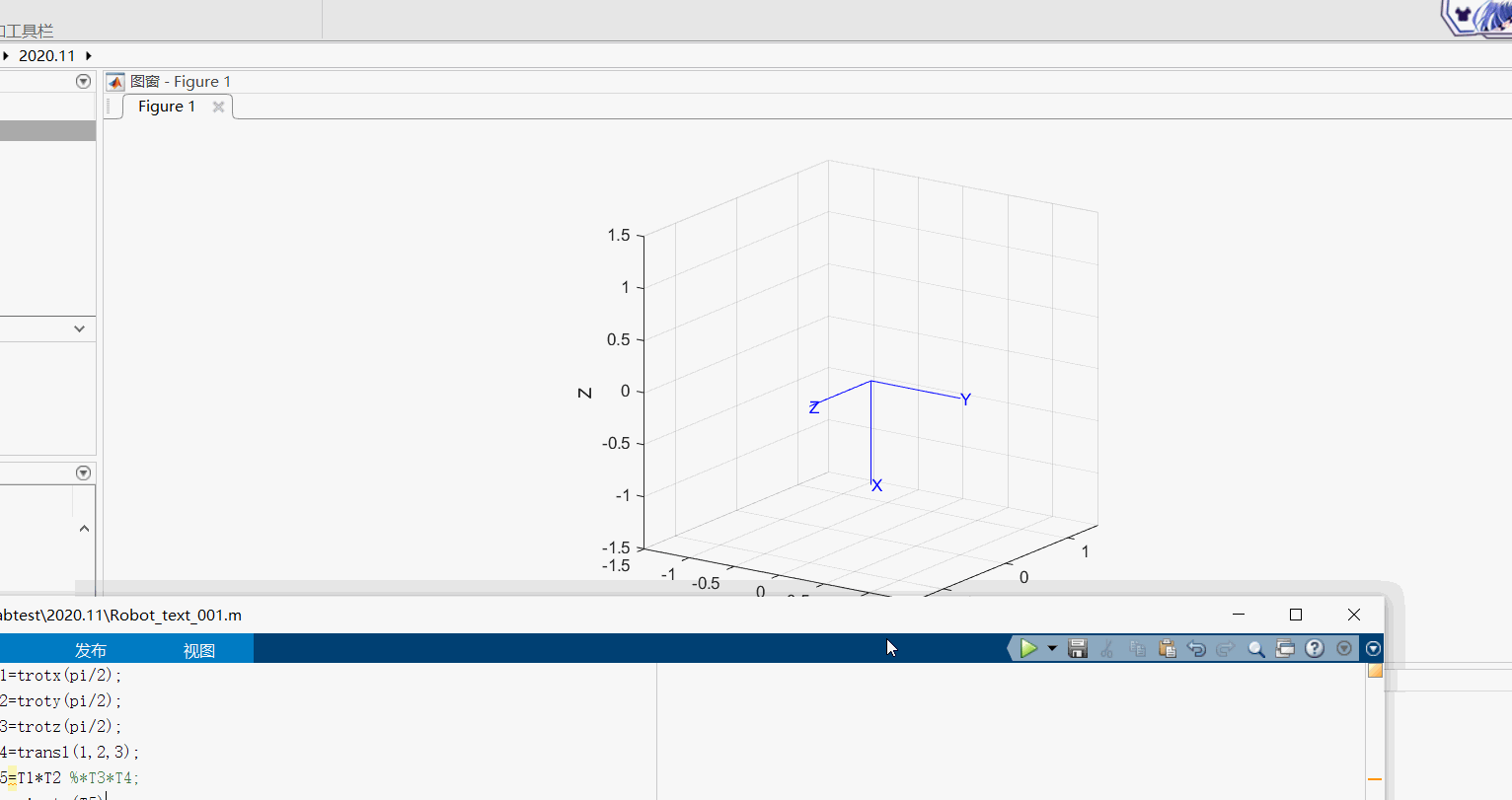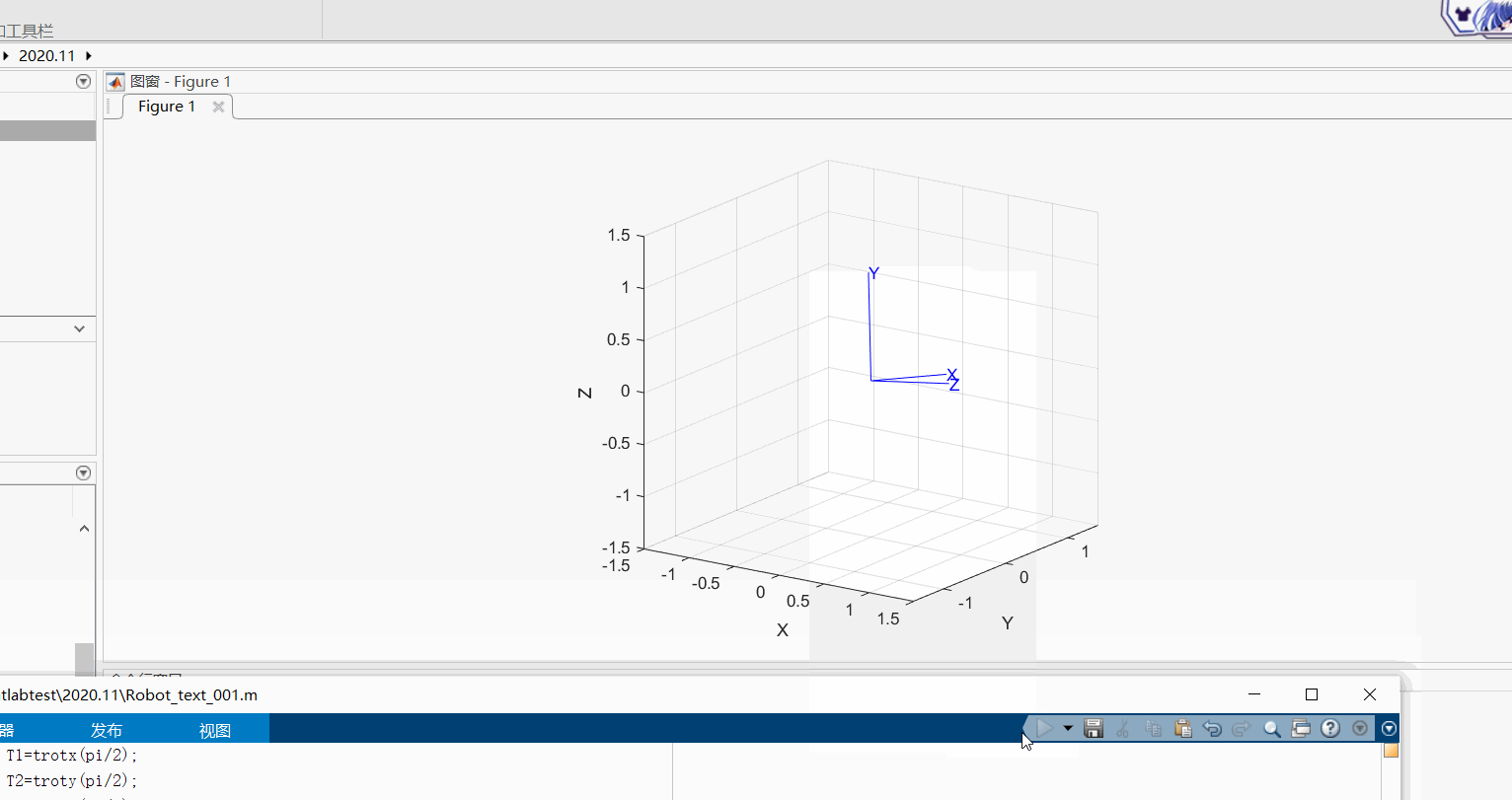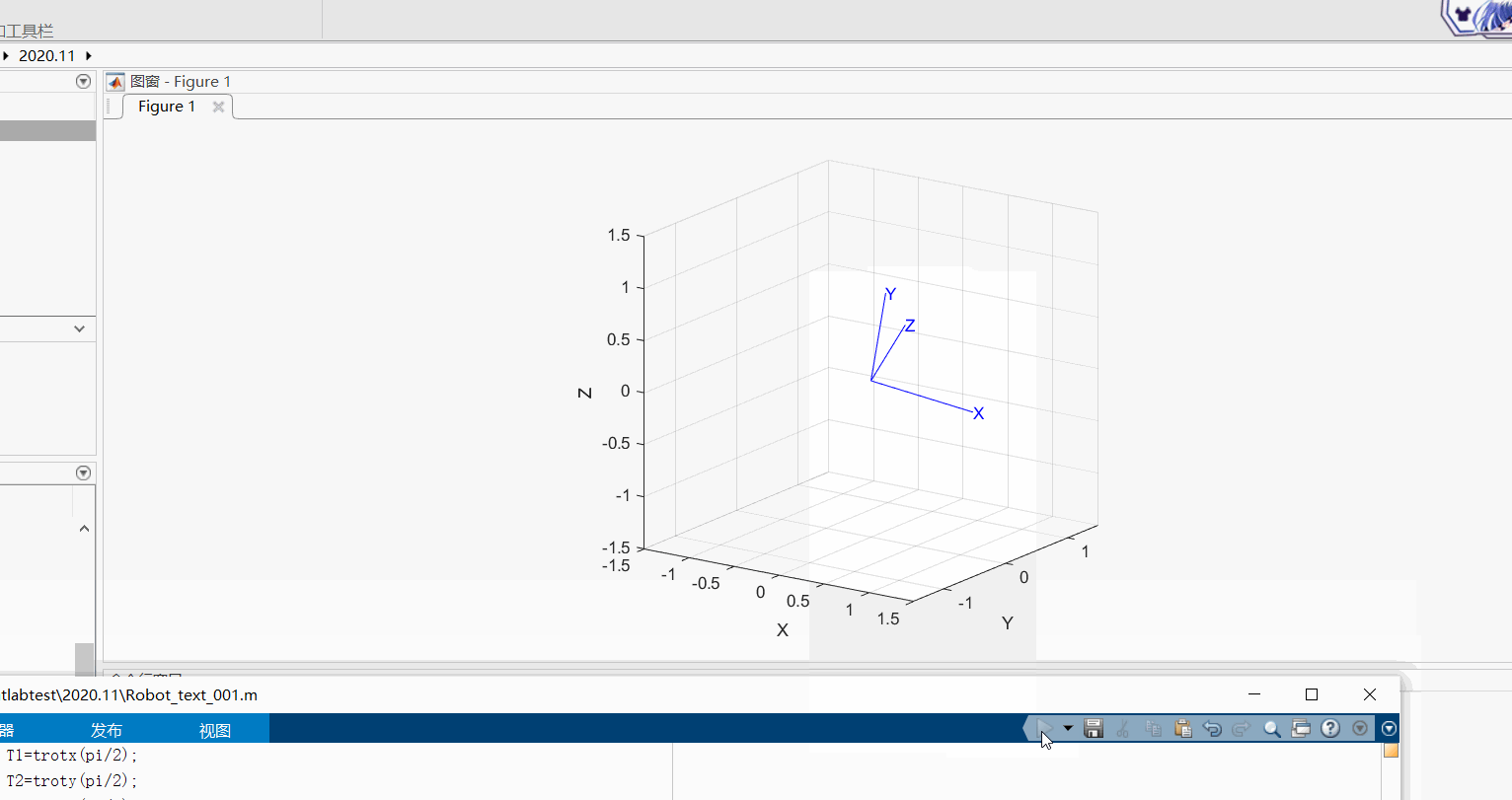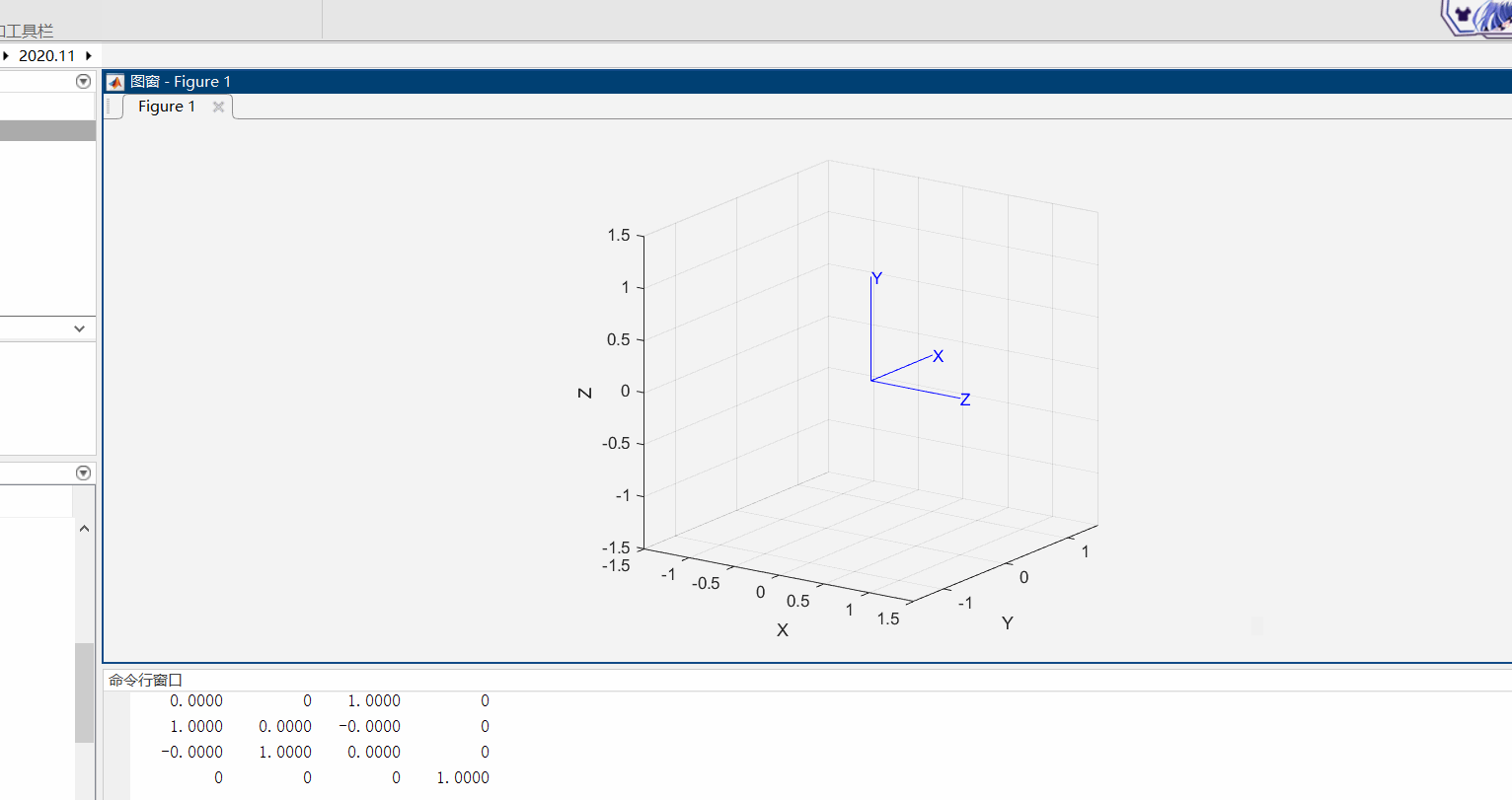
(1)绕动坐标系进行旋转,比如先绕X轴旋转π/2,再绕新的Y轴旋转π/2 。(此种旋转方式等效于先绕定坐标系Y轴旋转π/2,再绕定坐标系的X轴旋转π/2)
T1=trotx(pi/2);
T2=troty(pi/2);
T5=T1*T2;
tranimate(T5)
(2)先在在X方向平移1,在Y方向平移2,在Z方向上平移3,再绕动坐标系进行旋转,比如先绕X轴旋转π/2,再绕新的Y轴旋转π/3
T1=trotx(pi/2);
T2=troty(pi/3);
T3=transl(1,2,3);
T4=T3*T1*T2;
tranimate(T4)

5、各种姿态表示方法之间的转化
(1)从欧拉角直接转换为旋转矩阵 用eul2r()函数,如:
R=eul2r(0.1,0.2,0.3)
(2)从旋转矩阵求欧拉角,用tr2eul()函数,如:
gamma = tr2eul(R)
(3)从旋转矩阵求RPY角,用tr2rpy()函数,如:
R1 = rpy2r(0.1, 0.2, 0.3)
gamma = tr2rpy(R1)



















