leetcode python刷题记录（十一）（101~110）

leetcode python刷题记录（十一）（101~110）

101. 对称二叉树

class Solution:
    # 在【100. 相同的树】的基础上稍加改动
    def isSameTree(self, p, q):
        if p is None or q is None:
            return p is q
        return p.val == q.val and self.isSameTree(p.left, q.right) and self.isSameTree(p.right, q.left)

    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        return self.isSameTree(root.left, root.right)

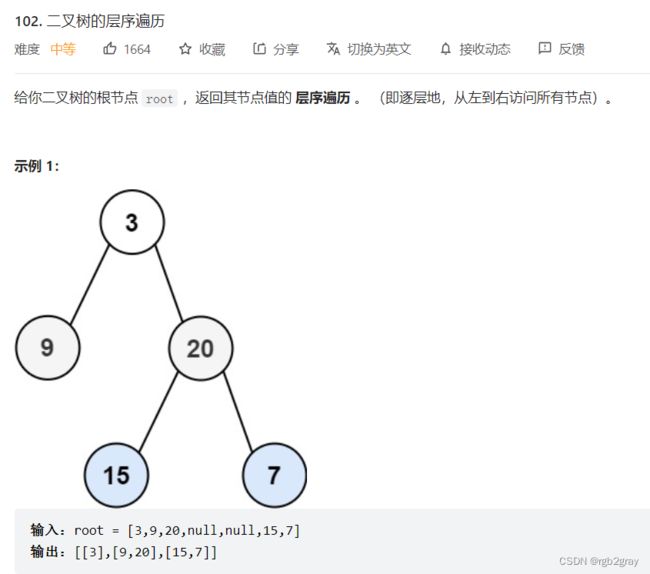
102. 二叉树的层序遍历

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        queue=[root]
        res=[]

        while queue:

            res.append([node.val for node in queue]) #存储当前层的孩子节点列表
            temp=[]

            for node in queue:
                if node.left:
                    temp.append(node.left)
                if node.right:
                    temp.append(node.right)

            queue=temp #后把queue更新成下一层的结点，继续遍历下一层

        return res

103. 二叉树的锯齿形层序遍历

class Solution:
    def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        
        if root is None:
            return []
        ans = []
        cur = [root]
        even = False
        while cur:
            nxt = []
            vals = []
            for node in cur:
                vals.append(node.val)
                if node.left:  nxt.append(node.left)
                if node.right: nxt.append(node.right)
            cur = nxt
            ans.append(vals[::-1] if even else vals)
            even = not even
        return ans
            

104. 二叉树的最大深度

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root == None:
            return 0
        
        queue=[root]
        depth=0

        while queue:
            # 当前层的节点数
            n=len(queue)
            # 弹出当前层的所有节点，并将所有子节点入队列
            for _ in range(n):
                node=queue.pop(0)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

            depth=depth+1

        return depth

105. 从前序与中序遍历序列构造二叉树

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder or not inorder:
            return 
        
        root=TreeNode(preorder[0])  # 先序为“根左右”，所以根据preorder可以确定root
        idx=inorder.index(preorder[0])  # 中序为“左根右”，根据root可以划分出左右子树

        root.left=self.buildTree(preorder[1:idx+1],inorder[:idx])
        root.right=self.buildTree(preorder[idx+1:],inorder[idx+1:])

        return root

106. 从中序与后序遍历序列构造二叉树

和上一题类似：

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if not inorder or not postorder:
            return
        
        root=TreeNode(postorder[-1])
        idx=inorder.index(root.val)

        root.left=self.buildTree(inorder[:idx],postorder[:idx])
        root.right=self.buildTree(inorder[idx+1:],postorder[idx:-1])

        return root

107. 二叉树的层序遍历 II

class Solution:
    def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
        # 层序遍历后倒序输出即可
        if root == None:
            return []
         
        queue=[root]
        res=[]

        while queue:
            res.append([node.val for node in queue])
            temp=[]

            for node in queue:
                if node.left:
                   temp.append(node.left)
                if node.right:
                     temp.append(node.right)

            queue=temp

        return res[::-1]

108. 将有序数组转换为二叉搜索树

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        # 直接获取有序数组中值作为根就可以，递归生成左子树和右子树即可
        if len(nums)==0: return
        elif len(nums)==1: return TreeNode(nums[0])
        
        mid = len(nums)//2
        node=TreeNode(nums[mid])
        node.left=self.sortedArrayToBST(nums[:mid])
        node.right=self.sortedArrayToBST(nums[mid+1:])
    
        return node

109. 有序链表转换二叉搜索树

class Solution:
    def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:
        if not head:
            return None
        
        # 求链表长度
        p,n=head,0
        while p:
            p=p.next
            n=n+1

        if n == 1: return TreeNode(head.val)

        # 得到中点
        cur=head
        for _ in range(n//2-1):
            cur=cur.next

        # 建立二叉树
        root=TreeNode(cur.next.val)

        root.right=self.sortedListToBST(cur.next.next)
        cur.next=None
        root.left=self.sortedListToBST(head)

        return root

110. 平衡二叉树

递归计算每棵树的最大深度，当递归完当前节点的左子树的最高高度 l 和右子树的最高高度 r 时，若存在|l - r| > 1则标记整个二叉树不是一颗平衡二叉树

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        self.res=True
        self.dfs(root)
        return self.res

    def dfs(self,root):
        if not root:
            return 0
        lh=self.dfs(root.left)
        rh=self.dfs(root.right)
        if abs(lh-rh) > 1:
            self.res=False
        
        return max(lh,rh)+1