算法：静态查找表

查找表（Search table）是由同一类型的数据元素（或记录）构成的集合。关键字(key)是数据元素中某个数据项的值，又称为键值，用它可以表示一个数据元素，也可以标识一个记录的数据项（字段），称之为关键码。若此关键字可以唯一地标识一个记录，则称此关键字为主关键字（primary key)。而对于那些可以识别多个数据元素（或记录）的关键字，称为次关键字（Secondary Key)，次关键字也可以理解为不以唯一标识一个数据元素（或记录）的关键字，它对应的数据项就是次关键码。

查找（Searching)就是根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素（或记录）。

查找表按照操作方式来分有两大种：静态查找表和动态查找表。

静态查找表(Static Search Table) ：只作查找操作的查找表，主要操作为：

（1）查询某个“特定的”数据元素是否在查找表中。

（2）检索某个“特定的”数据元素和各种属性。

动态查找表（Dynamic Search Table)：在查找过程中同时插入查找表中不存在的数据元素，或者从查找表中删除已经存在的某个数据元素。

（1）查找时插入数据元素。

（2）查找时删除数据元素。

本文先来说说静态查找表。

一、顺序表查找

顺序查找（Sequential Search)又叫线性查找，是最基本的查找技术，它的查找过程是：从表中的一个（或最后一个）记录开始，逐个进行记录的关键字和给定值比较，若某个记录的关键字和给定值相等，则查找成功，找到所查的记录；如果直到最后一个（或第一个)记录，其关键字和给定值都比较不相等时，则表中没有所查的记录，查找不成功。

二、有序表查找

1、折半查找

折半查找（Binary Search)技术，又称为二分查找。它的前提是线性表中的记录必须是关键码有序（通常从小到大有序），线性表必须采用顺序存储。折半查找的基本思想是：在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找；若给定值大于中间记录的关键字，则在中间记录的右半区继续查找。不断重复上述过程，直到查找成功，或所有查找区域无记录，查找失败为止。

2、插值查找

插值查找（Interpolation Search)是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法，其核心就在于插值的计算公式 (key-a[low])/(a[high]-a[low]) 。

3、斐波那契查找

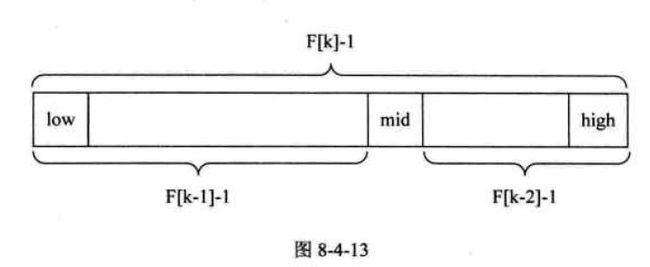
斐波那契查找（Fibonacci Search)算法的核心在于

1）当key = a[mid] 时，查找就成功；

2）当key < a[mid] 时，新范围是第low 个到第mid - 1个，此时范围个数为F[k-1]-1个。

3）当key > a[mid] 时，新范围是第m+1 个到第high个，此时范围个数为F[k-2]-1个。

如图8-4-13所示。

示例代码如下：（改编自《大话数据结构》）

#include
using namespace std;

#define INFINITLY 65535
#define MAXSIZE 100

int F[100]; /* 斐波那契数列 */

/* 无哨兵顺序查找，arr为数组，n为要查找的数组个数，key为要查找的关键字 */
/* 返回元素的位置pos (下标+1）*/
int Sequential_Search(int *arr, int n, int key)
{
    for (int i = 0; i < n; i++)
        if (arr[i] == key)
            return i + 1;
    return INFINITLY; //返回无穷说明失败
}

/* 有哨兵顺序查找 */
/* 返回元素的位置pos (下标+1）*/
int Sequential_Search2(int *arr, int n, int key)
{
    arr[n] = key;
    int i = 0;
    while (arr[i] != key)
        i++;
    return i + 1; //返回n+1 则说明失败
}
/* 折半查找 */
/* 返回元素的下标 */
int Binary_Search(int *arr, int n, int key)
{
    int low = 0;/* 定义最低下标为记录首位 */
    int high = n - 1;/* 定义最高下标为记录末位 */
    int mid;
    while (low <= high)
    {
        mid = (low + high ) / 2;/* 折半 */
        if (key < arr[mid])/* 若查找值比中值小 */
            high = mid - 1;/* 最高下标调整到中位下标小一位 */
        else if (key > arr[mid])/* 若查找值比中值大 */
            low = mid + 1;/* 最低下标调整到中位下标大一位 */
        else
            return mid;/* 若相等则说明mid即为查找到的位置 */
    }
    return INFINITLY;
}
/* 插值查找 */
int Interpolation_Search(int *arr, int n, int key)
{
    int low = 0;
    int high = n - 1;
    int mid;
    while (low < high)
    {
        /* 插值公式 */
        mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]);
        if (key < arr[mid])
            high = mid - 1;
        else if (key > arr[mid])
            low = mid + 1;
        else
            return mid;
    }
    return INFINITLY;
}

/* 斐波那契查找 */
int Fibonacci_Search(int *arr, int n, int key)
{
    int low = 0;/* 定义最低下标为记录首位 */
    int high = n - 1;/* 定义最高下标为记录末位 */
    int i, k = 0;
    int mid;

    while (n > F[k] - 1)
        k++;
    for (i = n - 1; i < F[k] - 1; i++)
        arr[i] = arr[n - 1];

    while (low <= high)
    {
        mid = low + F[k - 1] - 1;
        if (key < arr[mid])
        {
            high = mid - 1;
            k = k - 1;
        }
        else if (key > arr[mid])
        {
            low = mid + 1;
            k = k - 2;
        }
        else
        {
            if (mid <= n - 1)
                return mid;
            else
                return INFINITLY;
        }
    }

    return INFINITLY;
}

int main(void)
{
    int arr[MAXSIZE] = {1, 16, 24, 35, 47, 59, 62, 73, 88, 99};
    int result = Sequential_Search(arr, 10, 24);
    if (result != INFINITLY)
        cout << "24 's pos : " << result << endl;

    result = Sequential_Search2(arr, 10, 59);
    if (result != sizeof(arr) / sizeof(arr[0]))
        cout << "59 's pos : " << result << endl;

    result = Binary_Search(arr, 10, 73);
    if (result != INFINITLY)
        cout << "73 's pos : " << result + 1 << endl;

    result = Interpolation_Search(arr, 10, 16);
    if (result != INFINITLY)
        cout << "16 's pos : " << result + 1 << endl;

    F[0] = 0;
    F[1] = 1;
    for(int i = 2; i < 100; i++)
    {
        F[i] = F[i - 1] + F[i - 2];
    }

    result = Fibonacci_Search(arr, 10, 88);
    if (result != INFINITLY)
        cout << "88 's pos : " << result + 1 << endl;

    return 0;
}

复制

输出为：