树状数组（周灵猪）

首先分享我看的网址

树状数组 + 线段树+ 分块原理入门讲解 + 树状数组模版题_哔哩哔哩_bilibili

线段树用分治法；

树状数组模板：

int lowbit(int x){

return x&-x;

}

void (int idx,int v){//idx是加的区域的位置，v是加的值

for(int i=idx;i<=N;i+=lowbit(i)){//因为是加，所以要+lowbit

trr[i]+=v;}

int getsum(int idx){//获得sum的话，是要每个lowbit值去掉最后一个1，直到没1为止；

sum=0;

for(int i=idx;i>=1;i-=lowbit(i))

sum+=trr[i];

}

------------------------------------------------分割线------------------------------------------------------------------------------

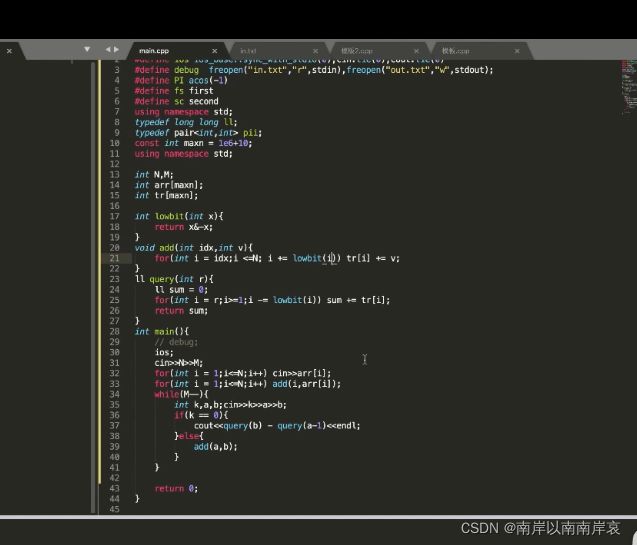
#include
#include
#include
#include
#include

using namespace std;
const int maxn = 1e6 + 10;

int N, M;
int arr[maxn];
int trr[maxn];
int lowbit(int x) {
    return x & -x;
}
void add(int idx, int v) {
    for (int i = idx; i <= N; i += lowbit(i))
        trr[i] += v;
}
int getSum(int idx) {
    int sum = 0;
    for (int i = idx; i >= 1; i -= lowbit(i))
        sum += trr[i];
    return sum;
}
int main(){
    cin >> N >> M;
    for (int i = 1; i <= N; i++) {
        cin>>arr[i];
    }
    for (int i = 1; i <= N; i++)//这个是建树
        add(i,arr[i]);
    while (M--) {
        int k, a, b;
        cin >> k >> a >> b;
        if (k == 0) {
            cout << getSum(b) - getSum(a - 1)<         }//（1,8]区域的总和所以后面减
        else {
            add(a, b);
        }
    }
    return 0;
}

单纯的加第a个数加V，则直接add（a，v），即可，

1264. 动态求连续区间和 - AcWing题库这个题要用到差分数组很怪，我用普通树状数组上去也时间超时，但是答案没错

-----------------------------------------分割线----------------------------------------------------

AcWing 242. 一个简单的整数问题-----维护差分数组的的树状数组模板题 - AcWing

那么例如给a[]a[]数组的[l,r][l,r]区间加上一个值，就可以给差分数组执行b[l]+=c,b[r+1]−=cb[l]+=c,b[r+1]−=c,

那么对应的add操作就是add(l,c),add(r+1,−c)add(l,c),add(r+1,−c)
如果是查询a[]a[]数组一个位置zz的值，那么只需要统计[1 z][1 z]这一段数组b的前缀和的值即可

---------------------------fengexian---------------------------------------------------------------------------------

逆序对的原理

n(81条消息) 离散化树状数组求逆序对_许久九的博客-CSDN博客https://blog.csdn.net/weixin_44171870/article/details/98614023?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164726363716780265424574%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=164726363716780265424574&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-11-98614023.142%5Ev2%5Epc_search_result_control_group,143%5Ev4%5Econtrol&utm_term=%E6%A0%91%E7%8A%B6%E6%95%B0%E7%BB%84%E6%B1%82%E9%80%86%E5%BA%8F%E5%AF%B9&spm=1018.2226.3001.4187

------------------------------------------分割线-----------------------------------------------------------------

差分数组（区域叠加）可以单独用，但是感觉树状数组和差分数组是适配的emmmm'

区域更新+区域查询》》》》》》树状数组加差分数组yyds

单个差分模板int n, m;
    for (int i = 1; i <= n; i++) {
        cin >> num[i];
    }
    for (int i = 1; i <= m; i++)
        trr[i] = num[i] - num[i - 1];
    for (int i = 1; i <= n; i++)
        num[i] = num[i - 1] + trr[i];

-----------------------------------------------------分割线-------------------------------

区间修改and区间查询

P4514 上帝造题的七分钟 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

高级树状数组——区间修改区间查询、二维树状数组 - 胡小兔 - 博客园 (cnblogs.com)

区间修改 区间查询模板

：

#include
#include
using namespace std;
const int maxn = 100010;
typedef long long  LL;
LL a[maxn], d[maxn], di[maxn], sum[maxn], n,m;
int lowbit(int x) {
    return x & (-x);
}
 void Add(LL a[], LL x, LL d)
 {
        while (x <= n)
        {
            a[x] += d;
            x += lowbit(x);
        }
  } 
LL Sum(LL a[], LL x)
    {
        LL sum = 0;
        while (x > 0)
        {
            sum += a[x];
            x -= lowbit(x);
        }
        return sum;
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = 1; i <= n; ++i)
        sum[i] = sum[i - 1] + a[i];

    while (m--) {
        int k,s, t, val;
        cin >> k;
        if (k == 1) {
            cin >> s >> t >> val;
            Add(d, s, val); //delta[s]=val
            Add(d, t + 1, -val);  //delta[t+1]=-val 
            Add(di, s, s * val);  //deltai[s]=i*val i是s
            Add(di, t + 1, -val * (t + 1));  //deltai[s]=-i*val i是t+1

        }

        else {
            cin >> s >> t;
            //整体的前i项和segma(org[i]) + (x+1)*segma(delta[i]) -segma(delta[i]*i)
            LL sum_a = sum[t] + (t + 1) * Sum(d, t) - Sum(di, t);
            LL sum_b = sum[s - 1] + s * Sum(d, s - 1) - Sum(di, s - 1);
            cout << sum_a - sum_b << endl;
        }
    }
}

(86条消息) 树状数组总结_丁磊_Ml的博客-CSDN博客