dp算法篇Day3

"梦却了无影踪，梦仍不曾改动"

---

        前面两篇dp算法篇，针对的问题都是单状态模式，即每个位置只有一种情况进行选择。那么在一个位置，面对多种情况又该作何选择呢？ 

        

11、按摩师

(1) 题目解析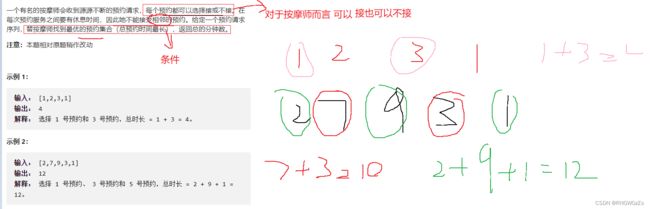

         对于某个位置，存在多种情况下，我们通常会增加一个dp表进行表示，切分子问题。

(2) 算法原理

class Solution {
public:
    int massage(vector& nums) {
        int n = nums.size();

        vector f(n+1,0);
        auto g = f;

        for(int i=1; i<=n; ++i){
            f[i] = nums[i-1] + g[i-1];
            g[i] = max(f[i-1],g[i-1]);
        }
        return max(f[n],g[n]);
    }
};

 

---

 

12、打家劫舍Ⅱ

(1) 题目解析

         如果做过打家劫舍1,会很明白其中的算法原理，这里无非是将当时的线性数组，转换为了循环数组。针对这类问题的首要方法，就是进行预处理！ 将循环数组，转换为线性数组。

(2) 算法原理

class Solution {
public:
    int _rob(vector& nums,int left,int right)
    {
        // 如果不够一个区间大小
        if(left > right) return 0;
   
        vector f(nums.size());
        auto g = f;

        f[left] = nums[left];
        // [left,right]
        for(int i=left + 1; i<=right; ++i){
            f[i] = nums[i] + g[i-1];
            g[i] = max(f[i-1],g[i-1]);
        }

        return max(g[right],f[right]);
    }
    
    int rob(vector& nums) {
        int n = nums.size();
        //                     从第三个开始~倒数的第二个   从第二个开始倒数的第一个
        return max(nums[0] + _rob(nums,2,n-2),_rob(nums,1,n-1));
    }
};

         注意区间的划分，这里划分的区间为 [left,right] 都时闭区间。

 

---

 

13、删除并获得点数

(1) 题目解析

(2) 算法原理

class Solution {
public:
    int deleteAndEarn(vector& nums) {
        const int NUM = 10001;
        
        // 预处理 将处理nums数组 转换为处理arr
        int arr[NUM] = {0};
        for(auto x:nums) arr[x] += x;

        vector f(NUM);
        auto g = f;
        // 因为 g[i] = max(f[i-1],g[i-1]) 此时与f[i]的大小知道与否无关
        f[0] = arr[0];

        for(int i=1; i

 

---

         

14、粉刷墙

(1) 题目解析

 

(2) 算法原理

class Solution {
public:
    int minCost(vector>& cost) {
        int n = cost.size();

        // N个房间 三种选择
        vector> dp(n+1,vector(3));

        for(int i=1 ; i<=n; ++i){
            dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + cost[i-1][0];
            dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + cost[i-1][1];
            dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + cost[i-1][2];
        }

        return min(min(dp[n][0],dp[n][1]),dp[n][2]);
    }
};

 

---

 

15、买卖股票的最佳时机含冷冻期

(1) 题目解析

(2) 算法原理

class Solution {
public:
    int maxProfit(vector& prices) {
        int n = prices.size();

        vector> dp(n,vector(3));
        // 初始化
        dp[0][0] = -prices[0];
        for(int i=1; i

 

---

本篇到此结束，感谢你的阅读。

祝你好运，向阳而生~