【论文阅读】（2013）Exact algorithms for the bin packing problem with fragile objects

---

论文来源：（2013）Exact algorithms for the bin packing problem with fragile objects
作者：Manuel A. Alba Martínez 等人

---

一、摘要

• 我们得到了一组物体，每个物体都具有重量和易碎性，以及大量没有容量的垃圾箱。
• 我们的目标是找到装满所有物体所需的最少垃圾箱数量，使每个垃圾箱中物体重量的总和小于或等于垃圾箱中物体的最小易碎性。
• 这个问题在文献中被称为易碎物品的装箱问题，并且出现在电信领域，当必须通过确保信道中的总噪声不超过一个电话。
• 我们提出了一种分支定界算法和几种分支价格算法来精确解决问题，并通过使用下界和量身定制的优化技术来提高它们的性能。
• 此外，我们还开发了相关易碎物品背包问题的最优解算法。
• 我们对基准实例集进行了广泛的计算评估，并表明所提出的算法表现非常好。

---

二、介绍

在易碎物品装箱问题 (BPPFO) 中，我们得到一组 $N=\{1,2,...,n\}$ 个对象和 $m$ 个容器。

每个对象 $j$ 的特征是重量 $w_j$ 和脆弱性 $f_j(j\in N)$，而箱子是无容量的。

BPPFO就是把所有的物体都装在最少数量的箱子里，保证每个箱子里的物体重量之和不超过物体的最小脆弱性。

更正式地说，让我们定义 $S(i)$ 分配给 bin $i(i=1,2,...,m)$ 的对象集。

BPPFO 的解决方案是可行的，如果每个对象都被准确地分配给一个箱子，并且对于任何箱子 $i$ 有：

在下文中，不失一般性，我们假设 $w_j\le f_j$，对于 $j\in N$，并且 $m$ 足够大以保证存在可行解（例如，$m=n$ 总是足够的）。我们还假设对象根据下式进行排序：

图 1(a) 描绘了一个包含 6 个对象的简单示例：对象 1 的权重为 2，脆弱性为 5，对象 2 的权重为 5，脆弱性为 6，依此类推。图 1（c） 显示了使用 4 个 bin 的最佳解决方案（暂时忽略图 1(b)）。

BPPFO 在电信中很重要，它模拟了蜂窝呼叫到频道的分配。

在码分多址(CDMA)系统中，网络被分成小区，每个小区配备有具有有限数量的频道的天线。每当用户拨打电话时，CDMA 系统都会将该呼叫分配到一个频道。

每个呼叫都以其产生的特定噪声为特征，并且对信道中的总噪声具有特定的容忍度。执行分配时必须考虑这些参数。事实上，许多呼叫可能被分配到同一信道，因为信道的带宽容量远大于任何呼叫的带宽需求，但这样的分配可能会在共享同一信道的呼叫之间产生干扰，因为噪声的总和可能太小。高，以保证良好的沟通。为此，要求频道中的总噪声不超过分配给该频道的任何呼叫的容限。

在 Bansal 等人的开创性论文中，CDMA 系统中分配呼叫的问题被建模为 BPPFO，方法是将频率信道与 bin 相关联，并且蜂窝呼叫对权重等于呼叫噪声和脆弱性等于呼叫的对象进行建模公差。通过求解 BPPFO，可以确定将蜂窝呼叫可行地分配给最少数量的频道。

BPPFO是一个难题。

考虑装箱问题(BPP)：给我们 $N$ 个重量为 $w_j(j\in N)$ 的物体和大量容量为 $C$ 的箱子，目的是将物体装入最少数量的箱子中，并确保物体重量之和不超过任何箱子的箱子容量。可以看出，BPP是一个特殊的BPPFO，其中对于所有 $j\in N$，$f_j=C$。

由于BPP是强N-P-hard，这同样适用于BPPFO。

值得一提的是，BPPFO在实践中也非常困难：有一些只有50个对象的基准测试实例没有被证明是最优的，参见Clautiaux等人。

请注意，有大量关于BPP的文献我们没有在本书中进行调查。

感兴趣的读者可以参考Valério de Carvalho等人、Clautiaux等人和Coffman等人。

我们只是提到一个事实，即BPP的最佳性能算法是基于分支和价格的，例如，参见 Alves和Valério de Carvalho 和Vanderbeck ，这确实是我们在这项工作中用来解决BPPFO的主要技术。

本文的目的就是给出BPPFO的精确算法。特别是，我们利用新的和现有的下限和上限技术，并将它们嵌入到特定的枚举方案中。我们提出了几个分支定价算法，这些算法以一致的方式提高了一组基准实例的最优解的数量。

在此过程中，我们还开发了具有脆弱对象的背包问题的有效算法，这是在为BPPFO生成列时要解决的从属问题。

---

三、之前在这个问题上的工作

Chan等人研究了BPPFO的在线版本，其中关于对象的信息仅在先前的对象已经被分配给bin之后才可用。他们通过近似方案解决了这个问题，并通过计算给出了一个简单的下界：

$L_1$ 可以在 $O(n)$ 中快速计算，但在实践中通常是不好的。

Bansal等人提出了一个更好的界限，称为 $L_2$ ，它基于以下组合问题的解决方案：

易碎物品的分式装箱问题(FBPPFO)是BPPFO的一种放松，在BPPFO中，允许将一个物品任意分成几块，并且这些块可以装入不同的箱子中。每一片都带有被切割物体的脆弱性。

回想一下，对象是按照非递减脆弱性排序的，即根据(2)。

Bansal等人证明了FBPPFO可以通过以下多项式算法精确求解：打开容量为 $f_1$ 的第一个容器，并将对象 $1$ 装入其中；对于任何连续的对象j，如果 $j$ 适合当前容器，则将 $j$ 装入其中，否则，仅将 $j$ 的适合部分装入当前容器，打开容量为 $f_j$ 的新容器，并将 $j$ 的剩余部分装入新容器。

在下文中，我们将把这个算法和它输出的值都称为 $L_2$ 。算法1中给出了 $L_2$ 的伪代码：

图1(b)报道了 $L_2$ 在图1(a)所示例子中的应用。一旦对象按照(2)排序，该算法的运行时间为$O(n)$。它在 $L_1$ 占主导地位，在实践中相当有效。

就数学模型而言，Clautiaux等人通过使用二进制变量 $y_i$ 将BPPFO建模为整数线性规划(ILP)，如果对象 $i$ 是其被打包的箱中具有最小脆弱性的对象，则 $y_i$ 取值1，否则取值$0(i\in N)$，如果对象 $j$ 被分配到具有作为最小脆弱性的对象 $i$ 的箱，则另一个二进制变量 $x_{ji}$ 取值 $1$ ，否则取值 $0(i=1，2，...，n，j=i+1，i+2，...，n)$。产生的ILP是：

目标函数(4)强制最小化箱的数量。约束(5)要求每个对象精确打包一次，约束(6)模拟脆性约束，约束(7)使模型线性松弛更紧。

Clautiaux等人也提出了一个基于BPP的经典集合覆盖公式的ILP。

他们定义一个模式，比如说 $p$，作为一组满足等式(1)的对象。$P$ 为所有模式的集合。

为了描述模式 $p$ ，他们使用向量 $(a_{1p}，a_{2p}，...a_{np})$ ，其中对于 $p\in P$，如果对象j在模式中，$a_{jp}$取值 $1$ ，否则取值 $0$ 。然后，他们引入二进制变量 $z_p$ ，如果使用模式 $P$ ，则取值 $1$ ，否则取值 $0$ ，对于 $p\in P$ ，并将BPPFO建模为：

目标函数(10)要求箱的数量最小化，约束条件(11)要求每个对象j被打包在至少一个箱中。

$P$ 的大小在对象数量上是指数级的，所以即使求解(10)–(12)的线性松弛也是困难的。

Clautiaux等人通过列生成算法解决了这个问题：他们放松了对线性的约束(12 ),并用模式子集初始化模型，然后他们迭代地添加具有负缩减成本的模式(如果有的话),直到找到最优(线性)解决方案。

为了确定负成本模式是否存在，需要解决的从属问题是一个特定的背包问题，它是用ILP模型解决的(见下面的4.1节)。

就上限而言，Bansal等人提出了一种2-近似贪婪启发式算法。Clautiaux等人提出了一个大集合的贪婪试探法和一个可变邻域搜索(VNS ),在基准实例集上获得了良好的结果。

总结文献中的结果，唯一精确的算法是基于ILP模型(4)-(9)的解的算法。在本文中，我们打算通过开发新的精确算法，使用文献中最成功的技术，并提出新的技术来弥补这一差距。

---

四、易碎物品背包问题的求解

我们定义两个组合问题：

• 在著名的0-1背包问题(KP01)中，$N$ 个利润为 $p_j$ 且重量为 $w_j(j\in N)$的对象必须被打包到一个容量为 $C$ 的箱子中，目的是确定一个总利润最大且总重量不超过 $C$ 的对象子集；
• 在具有易碎对象的0–1背包问题(KP01FO)中，具有利润 $p_j$ 、重量 $w_j$ 和脆弱性 $f_j (j ∈ N) $的 $N$ 个对象必须被打包到单个无容量的箱中，目的是确定总利润最大并且总重量不超过箱中任何对象的脆弱性的对象子集(根据(1))。

KP01是BPP的经典列生成算法中出现的从属问题。

KP01FO出现在BPPFO的列生成中(将在第五节中详细讨论)。

在介绍我们的分支定价算法之前，我们在这里描述三种精确求解KP01FO的算法：

4.1 ILP模型

KP01FO可以被建模(参见Clautiaux等人)为ILP，通过定义二进制变量 ${\beta }_j$ ，如果对象 $j$ 是容器中具有最小脆弱性的对象，则取值为1，否则取值为0，如果对象 $j$ 被打包在容器中，但不是具有最小脆弱性的对象，则取值为1，对于 $j\in N$，则取值为0。

约束(14)强加了箱内仅一个具有最小脆弱性的对象的存在，约束(15)对脆弱性限制进行建模，约束(16)强制两个变量族之间的关系(回想对象根据(2)进行排序)。

4.2 基于KP01的方法

我们称“见证”为bin中脆弱性最小的对象，即ILP模型(13)-(18)最优解中 ${\beta }_j=1$ 的对象 $j$ 。

KP01FO实例中的每个对象都是见证对象的候选对象。

我们可以一次尝试一个所有对象作为见证，评估每次尝试的总利润，然后保留最佳总利润作为原始KP01FO实例的最优解。

当给定对象 $j$ 是见证时可获得的总利润可以通过求解KP01实例来计算，其中容器容量固定为$f_j$ ，对象 $j$ 被强制放入容器中，并且其脆弱性小于 $f_j$ 的对象从实例中移除。

在实践中，我们用 $C=f_j-w_j$ 和对象集 $\{j+1，j+2，...，n\}$，然后把利润 $p_j$ 加到得到的解值上。

我们的算法在下文中表示为基于KP01，从对象1开始执行n次尝试，然后是对象2，依此类推。在每次尝试 $j$ 时，它求解刚刚定义的KP01实例，并使用得到的解来尽可能地改进迄今为止获得的最佳KP01FO解。一些简单的技术被用来加速这个过程。即，在给定的尝试 $j$：

• 我们通过移除 $w_k>f_j-w_j$ 的所有对象k来进一步减少当前对象集
• 让我们用 $z$ 表示在已经评估过的尝试中获得的最佳解。在调用精确的KP01算法之前，我们计算KP01解的上界，比如 $u$ ，如果 $u\le z$ ，那么我们跳过这个尝试。

在我们的实现中，$u$ 的值由Martello和Toth使用上限程序 $U_2$ 计算，KP01由Martello等人使用例程combo求解。

4.3 动态规划

众所周知，KP01可以通过动态编程(DP)算法来求解，该算法使用状态 $\psi (j，C)$ 来存储由前 $j$ 个对象和容量为 $C$ 的库给出的子实例的最优解。

对于 $c=0,...,C$，初始化 $\psi (0，c)=0$

这种递归对每个对象执行一个阶段，并且对于每个阶段考虑所有可能的箱大小，因此总的计算复杂度是 $O(nC)$ 。

KP01FO可以通过使用第4.2节的方法通过DP求解，包括求解最多n个KP01。对于被选作见证的每个对象 $j$ ，我们求解相应的KP01，将容器容量设置为 $f_j-w_j$ ，并相应地减少对象的子集。

最大值的KP01解就是最优KP01FO解。因此，该方法的总时间复杂度为 $O(n^2{f}_{max})$ ，其中 $f_{max}=ma{x}_{j\in N}\{f_j\}$ 。

通过不增加脆弱性来对对象进行分类可以获得更有效的方法。

在这种情况下，DP算法的唯一执行在 $O(n{f}_{max})$ 中求解KP01FO，如下所述：

命题1：让KP01FO实例的对象按非递增脆弱性排序，并应用递归(19)。KP01FO的最优解由下面的状态给出

证明1

---

五、二元分支方案

在这一节中，我们提出了两个分支定价(B&P)算法，用于求解第2节公式(10)到(12)的集合。由于公式中的列数呈指数增长，因此使用了经典的列生成方法，该方法最初由Gilmore和Gomory 针对BPP进行了描述。

我们提出的算法通过迭代调用第四节的算法，在枚举树的每个节点通过列生成解决公式的连续松弛，然后可能执行分支以获得整数解。

分支是B&P算法中非常关键的一点，因为在受限的主服务器(通常通过删除列)和从服务器(不能重新创建刚被删除的列)中都必须考虑额外的分支约束。有一些分支方案不会改变从属问题的结构，如Vanderbeck [7]中提出的方案。然而，对于这里提出的二进制方案来说，情况并非如此，二进制方案通常会影响从问题，并且可能具有很强的计算影响。在这一节的剩余部分，我们提出两个二进制分支方案和几个算法来解决由此产生的从属问题。

5.1 分支方案1（基于决策变量的分支）

5.2 分支方案2（基于yj和xji的分支）

5.3 将L2嵌入分支方案2

当一些变量已经通过分支固定时，具有可能理解节点的快速下限在计算上是有用的。我们通过用 $L_2$ 的修改版本在B&P-2树的给定节点求解FBPPFO(见第三节)来做到这一点。

在B&P-2中，我们首先将分数 $y_j$ 变量的值固定为整数值，而仅当所有 $y_j$ 都具有整数值时，我们才固定分数 $x_{ji}$ 变量的值。让我们考虑决策树的第一层，也就是我们只处理涉及 $y_j$ 变量的分支的那些层。

引理1：给定FBPPFO实例和n个元素的二进制向量y，考虑不等式：

当且仅当(24)成立时，FBPFFO具有见证集 $Y1=\{j\in N:y_j=1\}$ 的可行解。

命题2：具有强制和禁止见证集 $Y_1$ 和 $Y_0$ 的问题FBPPFO可以通过算法2来解决。

---

六、非二元分支方案

在这一节中，我们将介绍一些利用非二进制分支方案的算法，在该方案中，在每一层，一个对象被打包到一个容器中。

与第五节中给出的算法的主要区别在于，新方案不是基于当前(松弛)解的分数分量，而是使用预先指定的对象排序。

该方案在第6.1节中有详细的概述，还有一个组合分支限界。然后在5.2节中使用它来获得一个新的分支定价算法。

6.1 一种组合分枝定界算法

6.2 具有分支方案3的分支定价

---

七、计算结果

我们用C++对算法进行了编码，并在Clautiaux等人提出的基准集上对它们进行了测试。

这套工具在http://www.or.unimore.it/resources.htm,公开发售，由675个实例组成，分别包含50、100和200个对象，根据创建重量和易碎性的方式分为五类。

这个基准测试集尤其具有挑战性，因为它来自一系列长时间的计算测试。根据不同的标准创建了大量的实例，并对其进行了计算测试，然后只保留了五个最困难的实例类，并公开发布。

在测试中，我们使用了英特尔至强2.40 GHz处理器和6 GB内存。

所有LP和ILP模型都是在顺序模式下运行Cplex 12.2求解的。

在7.1节中，我们将介绍我们为寻找最佳B&P构型所做的研究。

在第7.2节中，将得到的B&P配置与BPPFO的其它精确算法进行了比较。

7.1 分支定价算法的设置和评估

我们需要评估分支方案的影响，用于解决从属问题的算法的影响，以及使用附加下限 $L_2^{01}$的影响。为了这个目标，我们在每个实例900 CPU秒的有限时间限制下运行我们算法的不同配置。

在表2中，我们给出了通过运行第5.1、5.2和6.2节的三个分支方案，使用三种不同的算法来求解从属关系而获得的结果。

该表显示了完整的675个实例集的聚合信息：行“gap”给出了算法提供的上限和下限之间的平均百分比差距，行“opt”给出了已证明的最佳解决方案的总数，行“sec”给出了平均CPU秒数(通过对所有实例(包括在时间限制处暂停的实例)花费的CPU秒数求和，然后除以675获得)。对于每个分支方案，opt的最佳值以粗体突出显示。

所有算法都是通过计算下限 $L_2$ (见算法1)和上限来初始化的，上限由Clautiaux等人的VNS试探法运行150 s给出，见第2节。该初始化阶段(其结果在表的第二列中给出)在大约82秒的平均时间内解决了312个优化实例，实现了2.27%的平均差距。

因此中的初始下限和上限是非常有效的，因为它们设法解决了几乎一半的测试实例以证明最优性。(注意，在经典的BPP中，对于已知的基准，没有被上下限解决的实例的数量小于10%,因此我们可以称我们的实例为具有挑战性的测试床。)

表中的其他三组列给出了三种B&P算法的结果，使用了从机的三种可能配置，即：ILP(见4.1节)、基于KP01(见4.2节)和DP(见4.3节)。当从属算法不可用于某个分支决策时，我们使用先前的算法。详细来说：

• B&P-1 运行了三次，分别使用了ILP、KP01基和DP；在基于KP01或DP不适用的节点中，使用ILP代替；
• B&P-2使用表1最后三栏中描述的三种配置运行；在DP不适用的节点中，使用基于KP01的 $x_0$ 来代替；
• B&P-3使用表1最后三列中标有“$y_i=1$”和“$x_{ji}=1$”的行中描述的三种配置运行。

在所有情况下，用 $n$ 列初始化受限主设备，每一列包含单个对象 $j$ ，加上属于由VNS找到的最佳启发式解决方案的列。

结果显示了三种分支方案的类似行为。基于KP01的算法大大改进了通过用Cplex求解ILP模型所获得的结果，导致更大数量的最优解、更小的间隙和CPU时间。反过来，DP改进了用基于KP01的算法获得的结果。在这种情况下，改进较小，但在所有分支方案上是一致的。基于这些结果，在剩余的测试中，所有算法都使用DP运行。

在表2中，还要注意平均CPU工作量比给定的时间限制要小得多，这表明如果找到了一个经过验证的最优解，那么它通常会在很短的时间内找到。这是由于初始试探法的良好性能和模型(10)-(12)的持续放松。事实上，考虑到B&P-3用DP找到的495个最优解，在428种情况下，证明的最优值等于初始启发式上界，在437种情况下，等于连续松弛的取整值。

表2中总结的B&P-2和B&P-3的所有测试都是使用 $L_2^{01}$ 运行的，以在调用更昂贵的列生成下限之前尽可能了解节点，请参见第4.3节和第5.2节。在表3中，我们将这些结果与不使用 $L_2^{01}$ 的结果进行了比较。同样在这种情况下，该表给出了675个实例的完整集合的聚合信息。可以注意到，对于两种分支方案，$L_2^{01}$ 的使用导致了小的但是一致的改进:它减少了平均差距和计算工作量，并且增加了解决证明的最优性的实例的数量。在剩下的测试中，所有的算法都使用 $L_2^{01}$ 运行。

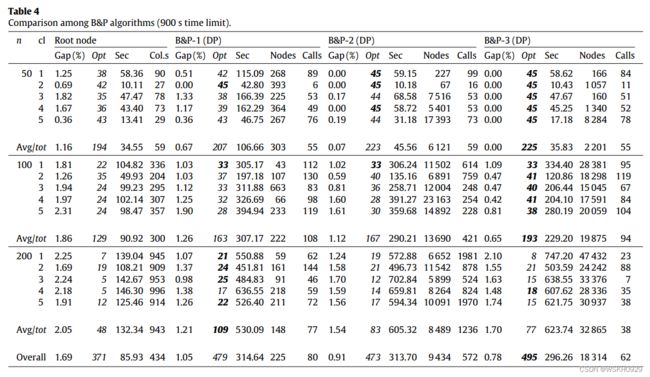
表4给出了我们从三种分支方案的三种最佳性能配置中获得的更详细的结果。第一列给出了对象的数量(“n”)和类的索引(“cl”)。对于n和cl的每个值，每行给出45个实例的合计信息。行“平均值/总数”给出了具有相同n值的225个实例的平均值/总数，而行“总数”给出了675个实例的完整集合的平均值/总数。

三个测试算法的根节点是相同的：用 $L_2$ 计算下界，用VNS试探法计算上界，通过第五节中描述的列生成方法(使用DP解决从属问题)解决模型(10)到(12)的连续松弛来改进下界。根节点的结果在第一组列中报告。除了“gap”、“opt”和“sec”具有与前面表格相同的含义之外，我们还在“col.s”中报告了在列生成结束时获得的模式集中包含的平均列数。根节点可以在大约 86 s的平均时间内解决371个证明的最优实例，导致1.69%的平均差距。对于只有50个对象的实例，平均列数通常很小，但是对于有200个对象的实例，列数会持续增加。

对于我们报告的三个分支方案，分别是“gap”、“opt”和“sec”，随后是枚举树探索的平均节点数(“nodes”)和每个节点对DP的平均调用数(“calls”)。节点和呼叫的平均值仅相对于由分支方案处理的实例进行评估，即，它们不考虑由根节点接近最优的371个实例。

B&P-1在解决由B&P-2和B&P-3支配的小规模实例(n = 50)时是无效的。同样，对于中型实例，与B&P-2和B&P-3相比，它的性能并不令人满意。另一方面，对于n = 200，B&P-1在所有五个类上都具有最好的计算性能，达到109个最优值，而B&P-2为83个最优值，B&P-3为77个最优值。B&P-1通常探测少量节点(平均225个)，并对DP执行少量调用(平均80个)。

B&P-3的行为与B&P-1相反。它在小规模实例上具有非常好的性能，所有这些实例都是在几秒钟内通过对根节点的额外努力而达到最优的。它在中等规模的实例上仍然有很好的性能(B&P-1的193次优化和B&P-2的167次优化)大型实例的性能较差。这种行为可以用这样一个事实来解释，即使用分数解来获得良好的分支方向仅对大规模实例有重要影响。B&P-3探测了大量的节点(平均超过18 000个),并且每个节点只需要少量的DP调用(平均只有62个)。

B&P-2在某种程度上介于B&P-1和B&P-3之间:它在小型实例上比B&P-1好，在大型实例上比B&P-3好。然而，它从来都不是“优胜”配置，这一结果可能是因为每个节点对DP的调用次数非常多(平均572次)。概括地说，我们从公开可用的基准实例集中获得的最佳B&P配置如下:

对于我们用更长的CPU时间执行的计算测试，这被证明是最好的配置。

我们以考虑脆弱性值对从解算法的影响来结束这一节。

由于DP算法以 $O(n{f}_{max})$ 运行，我们预计当 $f_{max}$ 的值变大时，它的性能会恶化。在基准实例集中，对于类别1、2、3、4和5，最大脆弱性分别等于450、750、750、450和600。

为了评估 $f_{max}$ 的增加实际上如何影响DP，我们对225个n = 50的小规模实例进行了一系列额外的测试，通过运行B&P-3和 $L_2^{01}$，使用三种可能的定价配置，并改变物品的重量和易碎性。特别地，在任何情况下，我们设置 $w_j=\mu w_j$ 和 $f_j=\mu f_j$ ，对于 $j=1，2，...，n$ ，并通过分别设置 $\mu$ 等于1、10和100来执行三个测试。这样，最优解不会改变，但是DP算法被迫执行更大的努力。

结果如表5所示，其中，对于所取的每个值和每个B&P-3配置，我们报告了optima的总数、平均差距、平均CPU秒数和一个附加信息 $se{c}_{pr}$ ，它给出了定价算法中一个实例所花费的平均时间。当$\mu$= 1时，没有变化影响基准实例，DP是最好的算法。当$\mu$= 10时，基于DP和KP01的行为大致相同。对于$\mu$= 100，DP的计算工作量平均增加到几乎4 s，因此基于KP01的算法成为性能最好的算法。在任何情况下，DP和基于KP01的算法都优于ILP，因为ILP是唯一不能在给定时间限制内解决所有实例的算法。

7.2 精确算法的比较

表6将上一节中获得的最佳B&P配置与BPPFO的其他精确算法进行了比较，即:Clautiaux等人的上下边界技术[2]、第2节的数学模型(4)-(9)以及第5.1节的B&B。如前所述，所有算法都用 $L_2$ 初始化，然后用150秒的VNS试探法进行初始化。如已经提到的，这种初始化解决了312个“较容易的”实例(见表2的第二列)的证明的最优性，并且让精确的算法在剩余的困难实例上工作。跟随

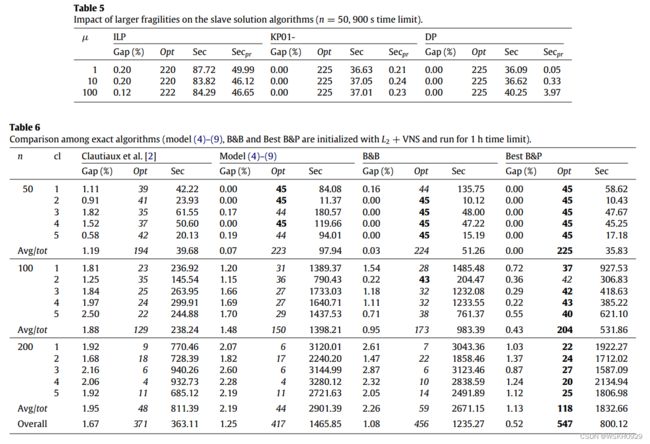
[2]中使用的设置我们运行数学模型、B&B和最佳B&P，每个实例的时间限制为1个CPU小时。这确保了与[2]中的下限和上限进行公平的比较，在我们在这项工作中使用的同一台PC上，上限和下限最多需要3200 s。

[2]中的算法很快，但仅获得371个最优值和1.67%的平均差距。用Cplex求解模型(4)到(9)将optima的总数提高到417。请注意，在这种情况下，在初始化中使用 $L_2$ 和VNS对模型非常有益，因为否则Cplex将只产生330个经过验证的最优解。还要注意，对于大的实例(n = 200 ), Cplex受[2]的下限和上限支配，这涉及间隙、时间和最优数量。

我们提出的B&B比前面两种方法产生更好的结果。除了一个有50个对象的实例之外，它以平均不到一分钟的计算量解决了几乎所有实例的最优化问题。它还用100个对象解决了173个实例，用200个对象解决了59个实例，但是在这些情况下，它需要相当大的平均时间。它总共解决了456个实例，但产生的平均差距仍然在1%以上。

B&P是平均计算性能最好的算法。除了具有n = 100和cl = 2的组(其中B&B胜过它)之外，它总是获得最高数量的已证明的最优值。

值得注意的是，它在大约半分钟内解决了n = 50的所有情况的最优解，并且获得了仅为0.52%的平均百分比差距。对于每个类的算法行为，我们注意到，对于前三种方法，类2是最简单的，而对于B&P，类3是最简单的。B&P表现出最稳定的行为，因为它是唯一一个始终为每个类解决100多个实例的算法。

---

八、总结

• 易碎物品的装箱问题是一个困难的组合问题，它模拟了电信中蜂窝电话到频道的分配。
• 在本文中，我们提出了一个分支定界算法和几个分支定价算法来精确求解该问题，并通过使用定制的优化技术来改进它们的行为。
• 在此过程中，我们还开发了有效的算法来解决带有易碎对象的背包问题。
• 我们在基准实例集上进行的计算评估表明，我们的算法性能非常好。
• 尽管如此，具有100个和200个对象的几个实例仍未被证明是最优的，因此未来对这个问题的研究是重要的。