KNN算法及应用场景
什么是KNN算法,KNN算法主要的的应用场景是什么?
KNN算法(K-Nearest Neighbor Algorithm)是一种基本的机器学习算法,它可以用于分类和回归任务。
在KNN算法中,给定一个新的输入样本,通过计算其与已知数据集中每个样本之间的距离,找到与其最相似的K个样本,然后通过这K个样本的分类信息(对于分类问题)或者平均值(对于回归问题)来预测该输入样本的分类或者数值。
KNN算法的主要优点是简单易用、适用于多分类问题、适用于非线性分类问题等。然而,它的主要缺点是计算复杂度高,特别是当数据集很大时,计算距离需要较多的时间和计算资源。
KNN算法的应用场景包括图像识别、语音识别、文本分类、推荐系统等。例如,KNN算法可以用于图像分类问题,其中每个图像可以看作是一个输入样本,它的特征可以表示为图像的像素值。通过计算每个图像与已知的训练集中的图像之间的距离,可以找到与其最相似的K个图像,然后通过这K个图像的分类信息来预测该图像的分类。
什么是KNN(K近邻算法)?【知多少】_哔哩哔哩_bilibili
KNN和上次使用的线性回归有哪些不同?
KNN和线性回归是两种不同的机器学习算法,它们在模型的构建和使用方法上有很大的差异:
模型类型:KNN是一种非参数模型,而线性回归是一种参数模型。
模型目标:KNN旨在通过寻找最近邻的样本来进行分类或回归预测,而线性回归旨在建立输入特征和目标变量之间的线性关系。
数据要求:KNN对数据的要求比较宽松,只需要样本具有可比性;而线性回归则要求样本符合线性关系。
计算方法:KNN算法需要计算新样本与每个训练样本之间的距离,然后找到最近的K个样本,对这K个样本进行加权求和或者多数表决来进行预测;而线性回归则是通过最小化目标变量与预测变量之间的误差平方和,来计算出回归系数和截距。
适用范围:KNN适用于多分类问题和非线性问题,如图像识别、文本分类等;而线性回归适用于连续数值预测问题,如房价预测、销售额预测等。
总之,KNN和线性回归是两种不同的机器学习算法,它们各有优缺点,适用于不同的场景和问题。在选择合适的算法时,需要考虑数据特征、模型要求和业务需求等多个因素。
利用KNN算法对橘子进行分类,Python代码实现
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
# 定义训练数据
X_train = np.array([[1.2, 3.5], [1.4, 3.2], [1.3, 3.6], [1.5, 3.9], [1.7, 3.6], [1.8, 3.2]])
y_train = np.array(['Orange', 'Orange', 'Orange', 'Orange', 'Orange', 'Orange'])
# 定义测试数据
X_test = np.array([[1.6, 3.4], [1.5, 3.5], [1.3, 3.3], [1.2, 3.7], [1.7, 3.4]])
# 定义KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)
# 拟合数据
knn.fit(X_train, y_train)
# 预测测试数据
y_pred = knn.predict(X_test)
# 打印预测结果
print(y_pred)![]()
在这个例子中,我们首先定义了一些训练数据和测试数据。训练数据包括6个橘子的特征(重量和直径),以及它们的分类标签(橘子)。测试数据包括5个橘子的特征,我们要使用KNN算法对这些橘子进行分类。
然后,我们定义了一个KNN分类器,并使用训练数据来拟合它。接着,我们使用KNN分类器对测试数据进行预测,并打印预测结果。在这个例子中,我们假设K值为3,也就是说,我们要找到距离测试数据最近的3个训练数据,并通过它们的分类标签来预测测试数据的分类。
请注意,这只是一个简单的示例,实际上,我们需要更多的训练数据和更多的特征来训练一个更准确的KNN分类器。
当然这个数据是写死的,当然我们从外界读取文件,我们只需要导入一个pandas库,然后引入读取即可
data = pd.read_csv('路径文件名',encoding='gbk')优化一下
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
def main():
# 定义训练数据
X_train = np.array([[1.2, 3.5], [1.4, 3.2], [1.3, 3.6], [1.5, 3.9], [1.7, 3.6], [1.8, 3.2]])
y_train = np.array(['Orange', 'Orange', 'Orange', 'Orange', 'Orange', 'Orange'])
# 定义测试数据
X_test = np.array([[1.6, 3.4], [1.5, 3.5], [1.3, 3.3], [1.2, 3.7], [1.7, 3.4]])
# 定义KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)
# 拟合数据
knn.fit(X_train, y_train)
# 预测测试数据
y_pred = knn.predict(X_test)
# 打印预测结果
print(y_pred)
if __name__ == "__main__":
main()这样,我们就使代码更加紧凑和易读,并使用了函数将重复代码封装为一个函数,从而避免了重复输入。
再优化,用图表来展示
# 请参照实验思路完成实训内容
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
def main():
# 定义训练数据
X_train = np.array([[1.2, 3.5], [1.4, 3.2], [1.3, 3.6], [1.5, 3.9], [1.7, 3.6], [1.8, 3.2]])
y_train = np.array(['Orange', 'Orange', 'Orange', 'Orange', 'Orange', 'Orange'])
# 定义测试数据
X_test = np.array([[1.6, 3.4], [1.5, 3.5], [1.3, 3.3], [1.2, 3.7], [1.7, 3.4]])
# 定义KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)
# 拟合数据
knn.fit(X_train, y_train)
# 预测测试数据
y_pred = knn.predict(X_test)
# 打印预测结果
print(y_pred)
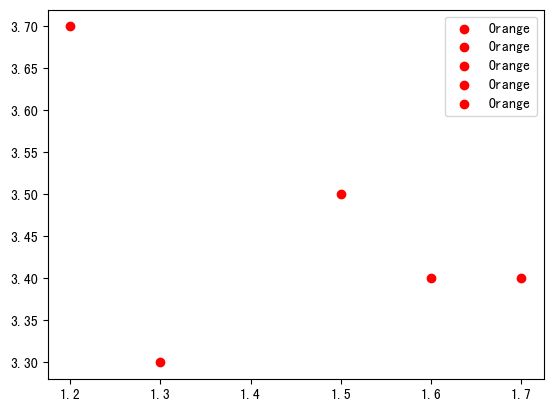
fig, ax = plt.subplots()
colors = {'Orange': 'red', 'Blue': 'blue'}
for i in range(len(X_test)):
ax.scatter(X_test[i][0], X_test[i][1], c=colors[y_pred[i]], label=y_pred[i])
ax.legend()
plt.show()
if __name__ == "__main__":
main()
这将创建一个新的窗口显示散点图。每个测试数据点都用一个点表示,并根据它们的预测类别用不同的颜色标记。