Computer Graphics From Scratch - Chapter 6

系列文章目录

简介：Computer Graphics From Scratch-《从零开始的计算机图形学》简介
第一章: Computer Graphics From Scratch - Chapter 1 介绍性概念
第二章：Computer Graphics From Scratch - Chapter 2 基本光线追踪
第三章：Computer Graphics From Scratch - Chapter 3 光照
第四章：Computer Graphics From Scratch - Chapter 4 阴影和反射
第五章：Computer Graphics From Scratch - Chapter 5 扩展光线追踪

---

---

Lines - 线条

In Part I of this book, we studied raytracing extensively and developed a raytracer that could render our test scene with accurate lighting, material properties, shadows, and reflection using relatively simple algorithms and math.
This simplicity comes at a cost: performance. While non-real-time performance is fine for certain applications, such as architectural visualization or visual effects for movies, it’s not enough for other applications, such as video games.

在本书的第一部分中，我们广泛研究了光线追踪，并开发了一种光线追踪器，它可以使用相对简单的算法和数学来渲染我们的测试场景，包括准确的光照、材质属性、阴影和反射。 这种简单性是有代价的：性能。 虽然非实时性能对于某些应用程序来说很好，例如建筑可视化或电影的视觉效果，但对于其他应用程序（例如视频游戏）来说还不够。

---

在本书的这一部分，我们将探索一组完全不同的算法，这些算法有利于性能而不是数学纯度。

我们的光线追踪器从相机开始，通过视口探索场景。 对于画布的每个像素，我们都会回答“场景的哪个对象在这里可见？”这个问题。 现在我们将采用一种在某种意义上相反的方法：对于场景中的每个对象，我们将尝试回答“该对象在画布的哪些部分可见？”这个问题。

事实证明，只要我们愿意在精度上做出一些权衡，我们就可以开发出比光线追踪更快地回答这个新问题的算法。 稍后，我们将探索如何使用这些快速算法来获得与光线追踪器相当的质量的结果。

我们将再次从头开始：我们有一个尺寸为 $C_w$ 和 $C_h$ 的画布，我们可以使用 PutPixel() 设置单个像素的颜色，但仅此而已。 让我们探索如何在画布上绘制最简单的元素：两点之间的线。

---

一、Describing Lines - 描述线

假设我们有两个画布点 $P_0$ 和 $P_1$，坐标分别为 $(x_0,y_0)$ 和 $(x_1,y_1)$。 我们如何绘制 $P_0$ 和 $P_1$ 之间的直线段？

让我们从用参数坐标表示一条线开始，就像我们之前对光线所做的那样（实际上，您可以将“光线”视为 3D 中的线）。 从 $P_0$ 开始，沿从 $P_0$ 到 $P_1$ 的方向移动一段距离，可以得到线上的任意点 $P$：

$$P=P_0+t(P_1-P_0)$$

我们可以将这个方程分解为两个，每个坐标一个：

$$x=x_0+t\cdot (x_1-x_0)-----①$$

$$y=y_0+t\cdot (y_1-y_0)-----②$$

让我们取第一个方程并求解 $t$：

$$x-x_0=t\cdot (x_1-x_0)$$

$$\frac{x-x_0}{x_1-x_0}=t$$

我们现在可以将 $t$ 的这个表达式代入第二个方程：

$$y=y_0+\frac{x-x_0}{x_1-x_0}\cdot (y_1-y_0)$$

稍微重新整理一下：

$$y=y_0+(x-x_0)\cdot \frac{y_1-y_0}{x_1-x_0}$$

请注意$\frac{y_1-y_0}{x_1-x_0}$是一个仅取决于端点的常数部分; 让我们称之为$a$[也就是我们好久之前学的斜率]。 所以我们可以将上面的等式改写为:

$$y=y_0+a\cdot (x-x_0)$$

---

什么是 $a$? 根据我们定义的方式，它测量每单位 x 坐标变化的 y 坐标变化； 换句话说，它是线斜率的度量。

让我们回到等式。 乘法分配律：

$$y=y_0+a\cdot x-a\cdot x_0$$

对常量进行分组：
$$y=a\cdot x+(y_0-a\cdot x_0)$$

同样，$(y_0–a{x}_0)$ 仅取决于段的端点； 让我们称之为b。 最后我们得到:
$$y=ax+b$$

---

这是线性函数的标准公式，几乎可以用来表示任何直线。 当我们求解 $t$ 时，我们直接除以 $x_1–x_0$ ，而不考虑如果 $x1=x0$ 会发生什么。 我们不能除以零，这意味着这个公式不能表示 $x_1=x_0$ 的线——即一条垂直的线。

为了解决这个问题，我们暂时忽略垂直线，稍后再弄清楚如何处理它们。

---

二、Drawing Lines - 画线

我们现在有一种方法可以获取我们感兴趣的每个 $x$ 值的 $y$ 值。这给了我们一个满足直线方程的 $(x,y)$ 对。

我们现在可以编写一个从 $P_0$ 到 $P_1$ 绘制线段的函数的第一个近似值。
设 $x_0$ 和 $y_0$ 分别是 $P_0$ 的 坐标， $x_1$ 和 $y_1$ 是 $P_1$ 的坐标。即： $P_0(x_0,y_0),P_1(x_1,y_1)$
假设 $x_0<x_1$，我们可以从$x_0$ 到 $x_1$，计算之间每个 $x$ 值以及其对应的 $y$ 值，并在这些坐标处绘制一个像素。

---

DrawLine(P0, P1, color) 
{
	a = (y1 - y0) / (x1 - x0)
	b = y0 - a * x0
	for x = x0 to x1 
	{
		y = a * x + b
		canvas.PutPixel(x, y, color)
	}
}

请注意，除法运算符$/$被期望执行实数除法，而不是整数除法。尽管在这种情况下$x$和$y$是整数，因为它们代表画布上的像素坐标。

---

另外 注意，我们认为for循环包括范围内的最后一个值。
在C、C++、Java和JavaScript等语言中，这将被写成$for（x=x_0;x<=x1;++x）$。
我们将在本书中使用这一约定。

这个函数是上述等式的直接、简单的实现。 它有效，但我们可以让它更快吗？

我们不会为任意 $x$ 计算 $y$ 的值。 相反，我们仅以 $x$ 的整数增量计算它们，并且我们是按顺序进行的。 在计算 $y(x)$ 之后，我们立即计算 $y(x+1)$：

$$y(x)=ax+b$$
$$y(x+1)=a\cdot (x+1)+b$$

我们可以稍微操作一下第二个表达式：

$$y(x+1)=ax+a+b$$
$$y(x+1)=(ax+b)+a$$
$$y(x+1)=y(x)+a$$

这不足为奇。 毕竟，斜率 $a$ 是当 $x$ 增加 $1$ 时 $y$ 变化的量度，这正是我们在这里所做的。

这意味着我们可以通过取 $y$ 的前一个值并加上斜率来计算 $y$ 的下一个值； 不需要逐像素乘法，这使函数更快。 一开始没有“$y$ 的先前值”，所以我们从 $(x_0,y_0)$ 开始。 然后我们继续将 $1$ 加到 $x$ 和 $a$ 到 $y$ 直到我们得到 $x_1$。

再次假设 $x_0<x_1$，我们可以将函数重写如下：

DrawLine(P0, P1, color) 
{
	a = (y1 - y0) / (x1 - x0)
	y = y0
	for x = x0 to x1 
	{
		canvas.PutPixel(x, y, color)
		y = y + a
	}
}

---

到目前为止，我们一直假设 $x_0<x_1$。 有一个简单的解决方法来支持不成立的线：因为我们绘制像素的顺序无关紧要，如果我们得到一条从右到左的线，我们可以交换 $P_0$ 和 $P_1$ 将其转换为 同一行的从左到右的版本，并像以前一样绘制它：

DrawLine(P0, P1, color) 
{
	// Make sure x0 < x1
	if x0 > x1 
	{
		swap(P0, P1)
	}
	a = (y1 - y0) / (x1 - x0)
	y = y0
	for x = x0 to x1 
	{
		canvas.PutPixel(x, y, color)
		y = y + a
	}
}

让我们用我们的函数画几条线。 图 6-1 显示了线段 $(–200,–100)–(240,120)$，图 6-2 显示了线段的特写.

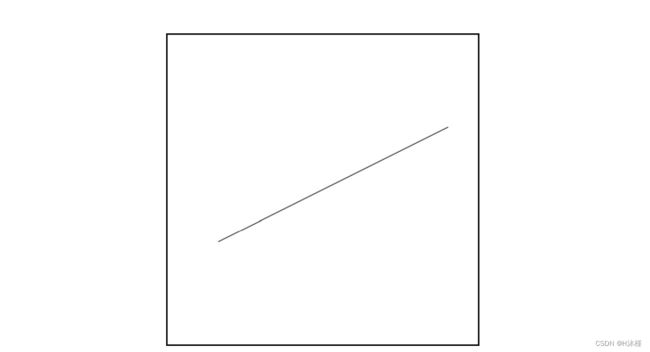
图 6-1：一条直线

图 6-2：放大直线

---

线条看起来是锯齿状的，因为我们只能在整数坐标上绘制像素，而数学线条实际上的宽度为零； 我们绘制的是从 $(–200,–100)–(240,120)$ 的理想线的量化近似值。

有一些方法可以绘制更漂亮的线条近似值（您可能想研究 MSAA、FXAA、SSAA 和 TAA 作为一组有趣的兔子洞的可能入口点）。 我们不会去那里有两个原因：（1）它更慢，（2）我们的目标不是画漂亮的线条，而是开发一些基本的算法来渲染 $3D$ 场景。

---

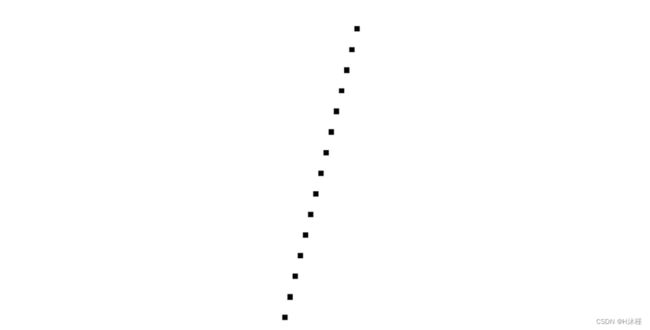
让我们试试另一行，$(–50,–200)–(60,240)$。 图 6-3 显示了结果，图 6-4 显示了相应的特写。

图 6-3：另一条斜率更高的直线

图 6-4：放大第二条直线

---

该算法完全按照我们告诉它的去做； 它从左到右，为每个 $x$ 值计算一个 $y$ 值，并绘制相应的像素。 问题是它为每个 $x$ 值计算了一个 $y$ 值，而在这种情况下，我们实际上需要为某些 $x$ 值计算几个 $y$ 值。

发生这种情况是因为我们选择了 $y=f(x);$ 的公式。 事实上，这也是我们不能画垂直线的原因——$y$ 的所有值都对应 $x$ 的相同值的极端情况。

---

三、Drawing Lines with Any Slope - 绘制任意斜率的线

选择 $y=f(x)$ 是任意选择； 我们同样可以选择将这条线表示为 $x=f(y)$。 通过交换 $x$ 和 $y$ 重新构造所有方程，我们得到以下算法：

DrawLine(P0, P1, color) 
{
	// Make sure y0 < y1
	if y0 > y1 
	{
		swap(P0, P1)
	}
	a = (x1 - x0)/(y1 - y0)
	x = x0
	for y = y0 to y1 
	{
		canvas.PutPixel(x, y, color)
		x = x + a
	}
}

这与之前的 DrawLine 相同，只是交换了 $x$ 和 $y$ 计算。 这个可以处理垂直线，并且可以正确绘制 $(0,0)–(50,100)$； 但当然，它根本无法处理水平线，或者正确绘制 $(0,0)-(100,50)$！ 该怎么办？

我们可以保留函数的两个版本，并根据我们尝试绘制的线选择使用哪一个。 标准很简单； 这条线的 $x$ 值是否比 $y$ 的不同值更多？ 如果 $x$ 的值多于 $y$，我们使用第一个版本； 否则，我们使用第二个。

示例6-1显示了一个处理所有情况的DrawLine的版本。

DrawLine(P0, P1, color) 
{
	dx = x1 - x0
	dy = y1 - y0
	if abs(dx) > abs(dy) 
	{
		// Line is horizontal-ish
		// Make sure x0 < x1
		if x0 > x1 
		{
			swap(P0, P1)
		}
		a = dy/dx
		y = y0
		for x = x0 to x1 
		{
			canvas.PutPixel(x, y, color)
			y = y + a
		}
	} 
	else 
	{
		// Line is vertical-ish
		// Make sure y0 < y1
		if y0 > y1 
		{
			swap(P0, P1)
		}
		a = dx/dy
		x = x0
		for y = y0 to y1 
		{
			canvas.PutPixel(x, y, color)
			x = x + a
		}
	}
}

示例6-1：一个处理所有情况的DrawLine的版本

这当然有效，但它并不漂亮。 有很多代码重复，选择使用哪个函数的逻辑，计算函数值的逻辑，以及像素绘制本身都是交织在一起的。 我们当然可以做得更好！

---

四、The Linear Interpolation Function - 线性内插函数

我们有两个线性函数 $y=f(x)$ 和 $x=f(y)$。 为了抽象出我们正在处理像素这一事实，让我们以更通用的方式将其写为 $d=f(i)$，其中 $i$ 是自变量，我们为其选择值，$d$ 是因变量 ，其值取决于另一个并且我们想要计算的那个。 在水平方向的情况下，$x$ 是自变量，$y$ 是因变量； 在垂直的情况下，情况正好相反。

当然，任何函数都可以写成 $d=f(i)$。 我们知道另外两件事完全定义了我们的函数：它是线性的，以及它的两个值——即 $d_0=f(i_0)$ 和 $d_1=f(i_1)$。 我们可以编写一个简单的函数来获取这些值并返回 $d$ 的所有中间值的列表，假设和之前一样 $i_0<i_1$：

Interpolate (i0, d0, i1, d1) 
{
	values = []
	a = (d1 - d0) / (i1 - i0)
	d = d0
	for i = i0 to i1 
	{
		values.append(d)
		d = d + a
	}
	return values
}

该函数与前两个版本的 DrawLine 具有相同的“形状”，但变量被称为 $i$ 和 $d$ 而不是 $x$ 和 $y$，并且这个函数不是绘制像素，而是将值存储在一个列表中。

注意$i_0$对应的$d$的值在$values[0]$中返回，$i_0+1$ 的值在$values[1]$中返回，以此类推； 通常，$i_n$ 的值在 $values[i_n-i_0]$ 中返回，假设 $i_n$ 在 $[i0,i1]$ 范围内。

我们需要考虑一个极端情况：我们可能想要为 $i$ 的单个值计算 $d=f(i)$，即当 $i_0=i_1$ 时。 在这种情况下，我们甚至无法计算 $a$，因此我们将其视为一种特殊情况：

Interpolate (i0, d0, i1, d1) {
	if i0 == i1 {
		return [ d0 ]
	}
	values = []
	a = (d1 - d0) / (i1 - i0)
	d = d0
	for i = i0 to i1 {
		values.append(d)
		d = d + a
	}
	return values
}

作为实现细节，对于本书的其余部分，自变量 $i$ 的值总是整数，因为它们代表像素，而因变量 $d$ 的值总是浮点值，因为它们代表泛型的值 线性函数。

现在我们可以使用 Interpolate 编写 DrawLine（示例 6-2）。

DrawLine(P0, P1, color)
{
	if abs(x1 - x0) > abs(y1 - y0) 
	{
		// Line is horizontal-ish
		// Make sure x0 < x1
		if x0 > x1 
		{
			swap(P0, P1)
		}
		ys = Interpolate(x0, y0, x1, y1)
		for x = x0 to x1 
		{
			canvas.PutPixel(x, ys[x - x0], color)
		}
	} 
	else 
	{
		// Line is vertical-ish
		// Make sure y0 < y1
		if y0 > y1 
		{
			swap(P0, P1)
		}
		xs = Interpolate(y0, x0, y1, x1)
		for y = y0 to y1 
		{
			canvas.PutPixel(xs[y - y0], y, color)
		}
	}
}

示例 6-2：使用 Interpolate 的 DrawLine 版本

---

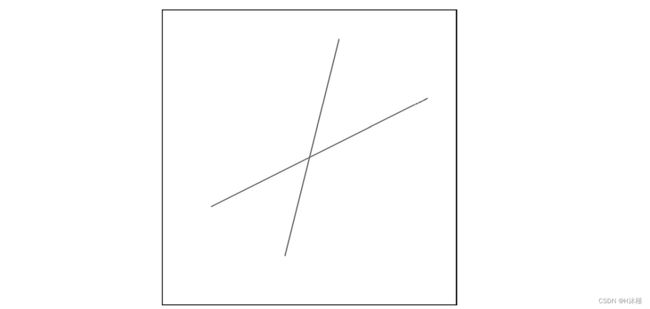
这个 DrawLine 可以正确处理所有情况（图 6-5）。

图 6-5：重构算法正确处理所有情况

---

您可以在以下位置查看此重构算法的现场演示https://gabrielgambetta.com/computer-graphics-from-scratch/demos/raster-02.html

---

虽然这个版本并不比前一个版本短很多，但它清晰地将 $y$ 和 $x$ 的中间值的计算与决定哪个是自变量以及像素绘图代码本身分开。

令人惊讶的是，这种线算法并不是最好的或最快的。 这种区别可能属于 Bresenham 算法。 提出这个算法的原因是双重的。 首先，它更容易理解，这是本书的首要原则。 其次，它为我们提供了 Interpolate 函数，我们将在本书的其余部分广泛使用它。

---

五、Summary - 概括

在本章中，我们已经迈出了构建光栅化器的第一步。 使用我们唯一的工具 PutPixel，我们开发了一种可以在画布上绘制直线段的算法。

我们还开发了插值辅助方法，这是一种有效计算线性函数值的方法。 在继续之前确保你理解它，因为我们会经常使用它。

在下一章中，我们将使用 Interpolate 在画布上绘制更复杂和有趣的形状：三角形。

---