【深度学习】2-2 神经网络 - 前向传播实现3层神经网络
神经网络分层
神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。
用图来表示神经网络的话,把最左边的一列称为输入层,最右边的一列称为输出层,中间的一列称为中间层。中间层有时也叫隐藏层(或隐含层)
实现3层神经网络
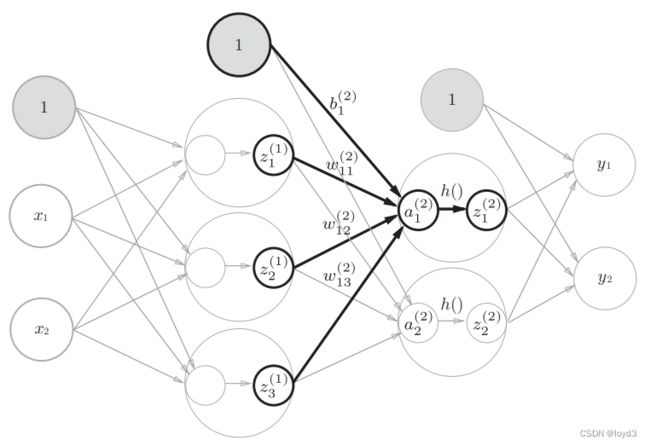
首先了解下权重符号的定义
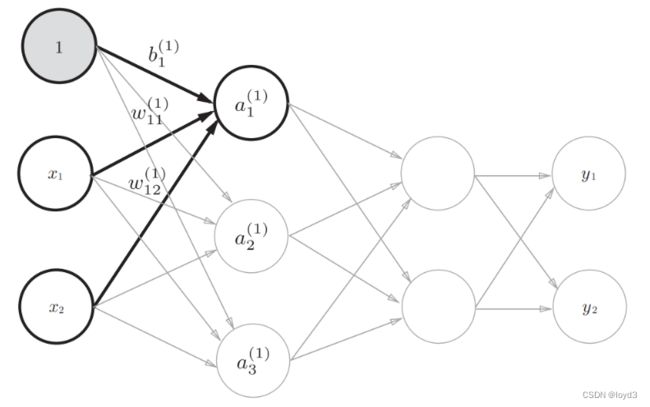
图中权重w
**上标 (1)**表示的是第1层的权重
下标 1 表示后一层的第1个神经元
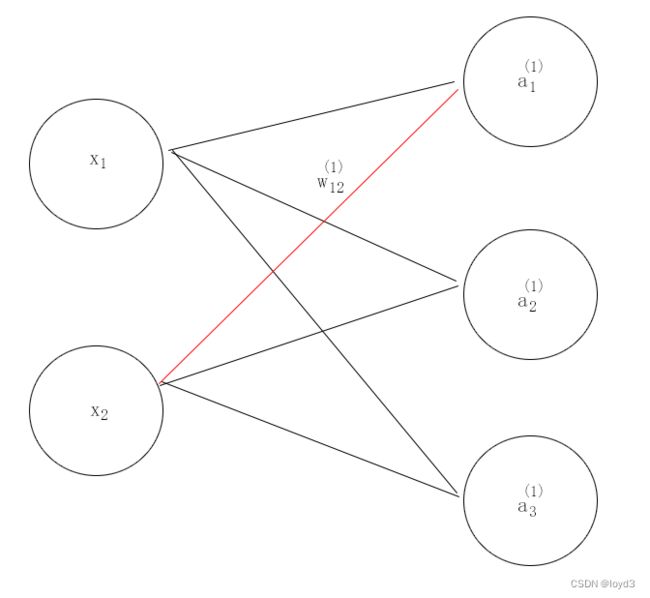
下标 2 表示前一层的第2个神经元
权重右下角按照“后一层的索引号、前一层的索引号”的顺序排列。
图中增加了表示偏置b的神经元“1”。请注意,偏置的右下角的索号只有一个。这是因为前一层的偏置神经元(神经元“1”)只有一个.
为了确认前面的内容,现在用数学式表示 a1,其通过加权信号和偏置按如下方式进行计算
a1(1) = w11(1) x1 +w12(1) x2+ b1(1)
如果使用矩阵的乘法运算,则可以将第1层的加权和表示成下面的式子
A(1) = XW(1)+ B(1)
其中,各参数的表示如下:
因为上标都是(1) 所以在下面的式子中省略(1)
A = ( a 1 a 21 a 31 ) (0) A= \begin{pmatrix} a~1~ & a~21~ & a~31~ \\ \end{pmatrix} \tag{0} A=(a 1 a 21 a 31 )(0)
X = ( x 1 x 2 ) (0) X= \begin{pmatrix} x~1~ & x~2~ \\ \end{pmatrix} \tag{0} X=(x 1 x 2 )(0)
B = ( b 1 b 2 b 3 ) (0) B= \begin{pmatrix} b~1~ & b~2~ & b~3~\\ \end{pmatrix} \tag{0} B=(b 1 b 2 b 3 )(0)
W = ( w 11 w 21 w 31 w 12 w 22 w 32 ) (0) W= \begin{pmatrix} w~11~ & w~21~ & w~31~ \\ w~12~ & w~22~ & w~32~ \\ \end{pmatrix} \tag{0} W=(w 11 w 12 w 21 w 22 w 31 w 32 )(0)
下面用NumPy多维数组来实现
X=np.array([1.0, 0.5])
W1 = np.array([0.1,0.3,0.5],[0.2,0.4,0.6])
B1=np.array([0.1,0.2,0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
A1 = np.dot(X,W1)+B1
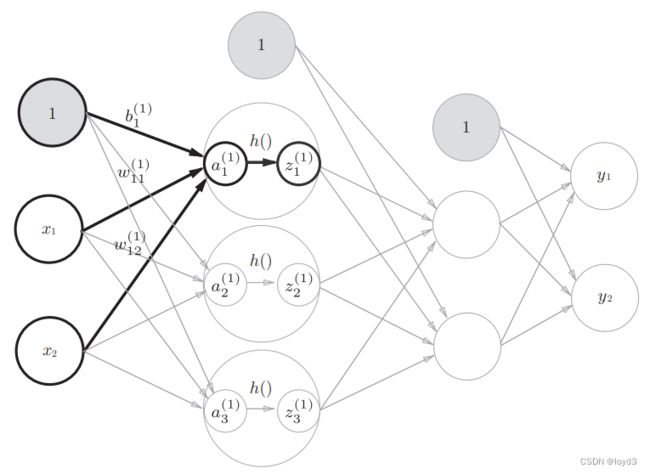
隐藏层的加权和(加权信号和偏置的总和)用a表示,被激活函数转换后的信号用z表示。此外,图中h()表示激活函数,这里我们使用的是sigmoid函数。
X=np.array([1.0, 0.5])
W1 = np.array([0.1,0.3,0.5],[0.2,0.4,0.6])
B1=np.array([0.1,0.2,0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
A1 = np.dot(X,W1)+B1
Z2 =sigmoid(A2)
最后是第2层到输出层的信号传递(图3-20)。输出层的实现也和之前的实现基本相同。不过,最后的激活函数和之前的隐藏层有所不同。
def identity_function(x):
return x
W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 =np.dot(Z2,W3)+ B3
Y=identity_function(A3) # 或Y=A3
identity_function()函数也叫恒等函数并将其作为输出层的激活函数。
另外要注意的是,在下图中输出层的激活函数用 σ()
表示,不同于隐藏层的激活函数h()
输出层所用的激活函数,要根据求解问题的性质决定
回归问题使用恒等函数 (回归一般用于预测,当然也可用于分类)
二元分类使用sigmoid函数
多元分类可以使用softmax函数
代码总结
def init_network():
network={}
network['W1'] = np.array([0.1,0.3,0.5],[0.2,0.4,0.6])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([0.1,0.4],[0.2,0.5],[0.3,0.6])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([0.1,0.3],[0.2,0.4])
network['b2'] = np.array([0.1,0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x=np.array([1.0,0.5])
y=forward(network, x)
print(y)
这样通过NumPy多维数组,可以实现神经网络
补充知识:
回归问题多用来预测一个具体的数值,如预测房价、未来的天气情况等等。例如我们根据一个地区的若干年的PM2.5数值变化来估计某一天该地区的PM2.5值大小,预测值与当天实际数值大小越接近,回归分析算法的可信度越高。