数字电子技术-组合逻辑电路
文章目录
- 一、组合逻辑电路的分析
- 二、组合逻辑电路的设计
- 三、组合逻辑中的竞争-冒险
- 四、若干典型的组合逻辑电路
-
- 4-1 编码器
-
- 4-1-1 普通编码器
- 4-1-2 优先编码器
- 4-1-3 典型编码器电路
- 4-2 译码器/数据分配器
-
- 4-2-1 二进制编码器
- 4-2-2 二-十进制译码器
- 4-2-3 显示译码器
- 4-2-4 数据分配器
- 4-3 数据选择器
- 4-4 数值比较器
-
- 4-4-1 一位数值比较器
- 4-4-2 多位数值比较器
- 4-5 算数运算电路
-
- 4-5-1 半加器和全加器
- 4-5-2 多位数加法器
一、组合逻辑电路的分析
- 组合逻辑电路:在任意时刻电路的输出仅取决于该时刻的输入,而与输入信号作用前电路所处的状态无关。
- 电路特点:无记忆,无反馈(组合逻辑电路中不包括锁存器和触发器等记忆单元)。
一般分析步骤:
- 根据给定的逻辑电路写出逻辑函数表达式。
由输入端开始逐级向后推导,对每个门写出其输出表达式,最后得出整个电路的输出与输入的逻辑函数。 - 列出真值表。
如果电路比较简单,通过表达式就可以直接知道电路的逻辑功能。但大部分情况下还必须由逻辑函数表达式列出真值表,再根据真值表来确定电路的逻辑功能。写真值表时要注意列出输入变量所有的取值组合。 - 分析得出电路的逻辑功能。
L的0、1比较集中,观察其大小规律。
L的0、1比较分散,考虑奇偶校验。
注:可以不一步一步写,在图中标注(个人觉得比较方便)
三位二进制数 A = A2A1A0(知到上的测验题)
二、组合逻辑电路的设计
要求:实现的电路要最简,即所用器件品种最少数量最少、连线最少.
一般设计步骤:
- (1)根据设计要求确定输入输出变量并逻辑赋值写出真值表。
用逻辑语言来描述实际问题。首先对设计要求进行分析,明确因果关系,确定输入输出变量;然后规定变量的赋值规则,即变量何时取1何时取0;最后根据这些逻辑关系写出真值表,真值表列写的是否完整、正确将直接影响到设计方案的最终结果。 - (2)由真值表写出逻辑函数表达式并化简或转换。
写出逻辑函数表达式后,需要根据实际设计来选择化简或变换的方式。
若使用小规模器件设计,可以将逻辑函数化最简形式,以使电路中所使用的门的个数最少。若使用中规模器件设计,则可以将逻辑函数变换成与所选用器件函数相类似的形式,以使电路中所使用芯片个数最少。 - (3)选用合适的器件画出逻辑图。
上述步骤在实际设计时可以根据需要进行调整。

例:设计一个交通灯故障自动检测器,以实现红、黄、绿三种灯的远程监控,要求用与非门实现。
注:需考虑交通灯逻辑
解:(1)逻辑赋值:
输入:红、黄、绿三种灯分别用变量A、B、C表示,灯亮为1,不亮为0。
输出:用变量L表示,正常为1,有故障为0。
(2)列出真值表
| A | B | C | L |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
(3)写出逻辑表达式
L = A ‾ B ‾ C + A ‾ B C ‾ + A B ‾ C ‾ L=\overline A\overline BC+\overline AB\overline C+A\overline B\overline C L=ABC+ABC+ABC
变换成与非式
L = A ‾ B ‾ C + A ‾ B C ‾ + A B ‾ C ‾ ‾ ‾ = A ‾ B ‾ C ‾ + A ‾ B C ‾ ‾ + A B ‾ C ‾ ‾ ‾ L=\overline{\overline{\overline A\overline BC+\overline AB\overline C+A\overline B\overline C}}=\overline{\overline{\overline A\overline BC}+\overline{\overline AB\overline C}+\overline{A\overline B\overline C}} L=ABC+ABC+ABC=ABC+ABC+ABC
(4)画出逻辑图
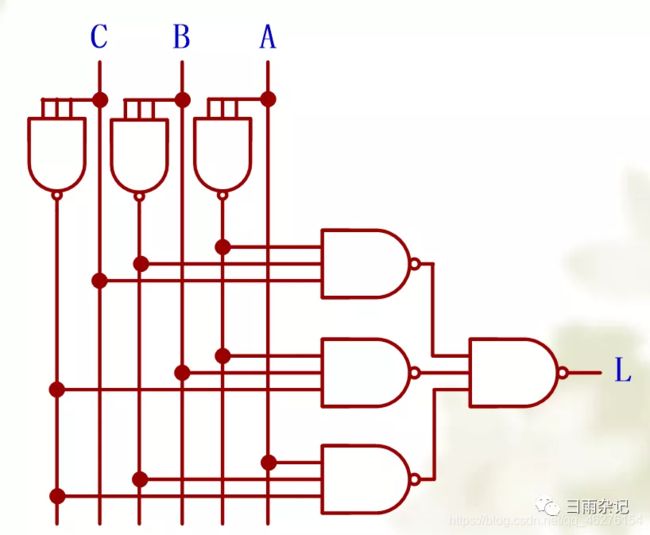
注意这种阵列画图的方法。
三、组合逻辑中的竞争-冒险
- 由于逻辑门电路存在延迟时间,且输入信号到达同一器件时所经历的路径也可能不同,从而引起几个输入信号到达同一地点时有先有后的现象,这种现象称为竞争。
- 竞争若使电路输出出现违背逻辑关系的尖峰脉冲(干扰脉冲或毛刺),即使得真值表所描述的逻辑关系受到短暂的破坏,就会产生错误的输出,称为冒险。
- 不是所有竞争都会引起错误输出(冒险),但在实际电路中信号的变化快慢有一定随机性,很难预测哪些信号变化会产生冒险,因此,只能说存在竞争就有可能产生冒险,这种现象就统称为竞争冒险。
0型冒险 L = X + X ‾ L=X+\overline X L=X+X 1型冒险 L = X ⋅ X ‾ L=X\cdot\overline X L=X⋅X
(1)冒险现象的判别
-
代数法
一般,具有竞争能力的变量(一般由非门产生),若其表达式具有 L = X ⋅ X ‾ L=X\cdot\overline X L=X⋅X的形式,则有可能产生1型冒险;若表达式具有 L = X + X ‾ L=X+\overline X L=X+X的形式,则有可能产生0型冒险。
方法:写出函数表达式后,先找出具有竞争能力的变量,然后求出其他逻辑变量的取值发生变化时的逻辑函数表达式,根据表达式中是否出现上述两种形式,来判别是否存在冒险及冒险的类别。
例:已知电路逻辑函数表达式为 L = ( A + B ‾ ) ( B + C ) L=(A+\overline B)(B+C) L=(A+B)(B+C)判断此电路是否存在冒险。
变量B具有竞争能力,将A、C的各种取值组合列出并求出对应表达式如下表所示。A C L 0 0 B ⋅ B ‾ B\cdot\overline B B⋅B 0 1 B B ‾ B\overline B BB 1 0 B B B 1 1 1 由表知,当A=C=0时,有 L = B ⋅ B ‾ L=B\cdot\overline B L=B⋅B
该电路可能发生1型冒险。 -
卡诺图法
凡在卡诺图中存在两个圈相切(相邻而不相交)处,都有可能产生冒险现象。
例: L = A C + B ‾ L=AC+\overline B L=AC+B

两圈相切处B=C=1,故当A变量变化时(A由0变1或由1变0时,即A由一个圈进入另一个圈的相邻项时)可能产生冒险。
(2)消除竞争冒险的方法
- 修改逻辑设计,增加冗余项或消去互补变量。
L = A C + A ‾ B L= AC+ \overline AB L=AC+AB
当B=C=1时存在0型冒险,增加冗余项:
L = A C + A ‾ B = A C + A ‾ B + B C L=AC+ \overline AB = AC+ \overline AB+BC L=AC+AB=AC+AB+BC
当B=C=1时,此时L恒为1,不会产生冒险。
可见,最经济的设计并不一定就是最佳万采,在最简的基础上,还需要能消除掉冒险。 - 引入选通脉冲
在电路中可能产生冒险的门电路上引入一个选通脉冲控制门打开的时刻。
当输入信号发生跳变时,选通脉冲S=1,使或门电路关闭,当输入稳定后,S=0,或门再打开,避免了冒险。 - 增加滤波电容
竞争冒险产生的干扰脉冲一般都很窄,通常在几十纳秒以内,如果逻辑电路工作速度不是很高,可以在输出端并联一个小的滤波电容,利用电容两端电压不能突变的特点来起到平滑的作用。
四、若干典型的组合逻辑电路
4-1 编码器
编码:将信息符号与二进制代码之间建立一一对应的关系。
编码器:能实现编码功能的逻辑电路。
二进制编码器:在某一时刻只把一个输入信号转换为n位二进制代码。
4-1-1 普通编码器
4-2线编码器
-
把4个输入信号编成对应的2位二进例代码输出的编码电路。
-
I 0 I 3 I_0~I_3 I0 I3为4个输入端,高电平有效;输出为两位二进制代码 Y 1 Y 0 Y_1Y_0 Y1Y0
I 3 I_3 I3 I 2 I_2 I2 I 1 I_1 I1 I 0 I_0 I0 Y 1 Y_1 Y1 Y 0 Y_0 Y0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 0 0 0 1 1 -
注意:编码器在任一时刻只能对一个输入信号进行编码。
-
输出表达式: Y 1 = I ‾ 3 I 2 I ‾ 1 I ‾ 0 + I 3 I ‾ 2 I ‾ 1 I ‾ 0 Y_1=\overline I_3I_2\overline I_1\overline I_0+I_3\overline I_2\overline I_1\overline I_0 Y1=I3I2I1I0+I3I2I1I0
Y 1 = I ‾ 3 I ‾ 2 I 1 I ‾ 0 + I 3 I ‾ 2 I ‾ 1 I ‾ 0 Y_1=\overline I_3\overline I_2 I_1\overline I_0+I_3\overline I_2\overline I_1\overline I_0 Y1=I3I2I1I0+I3I2I1I0 -
根据表达式:
如果某一时刻,有两个输入端如 I 1 I_1 I1、 I 2 I_2 I2,同时为1时,输出 Y 1 Y 0 Y_1Y_0 Y1Y0为00 ;而输出 Y 1 Y 0 Y_1Y_0 Y1Y0为00本应表示信号 I 0 I_0 I0。
4-1-2 优先编码器
4-2线优先编码器
- 功能表
I 3 I_3 I3 I 2 I_2 I2 I 1 I_1 I1 I 0 I_0 I0 Y 1 Y_1 Y1 Y 0 Y_0 Y0 0 0 0 1 0 0 0 0 1 × 0 1 0 1 × × 1 0 1 × × × 1 1 - 表达式: Y 1 = I 2 + I 3 Y_1=I_2+I_3 Y1=I2+I3 Y 0 = I ‾ 2 I 1 + I 3 Y_0=\overline I_2I_1+I_3 Y0=I2I1+I3
- 此时输出 I 1 I_1 I1、 I 2 I_2 I2即使同时为1,输出为10,仍然表示对优先级高的 I 2 I_2 I2的编码。
- 优先编码器实质就是对优先级最高的一个输入信号进行编码来避免输出紊乱。
4-1-3 典型编码器电路
- EI为输入使能端,EO为输出使能端,均为高电平有效。GS为优先编码器工作状态标志。
- 功能表:EI、 I 7 I_7 I7、 I 6 I_6 I6、 I 5 I_5 I5、 I 4 I_4 I4、 I 3 I_3 I3、 I 2 I_2 I2、 I 1 I_1 I1、 I 0 I_0 I0为输入端, Y 2 Y_2 Y2、 Y 1 Y_1 Y1、 Y 0 Y_0 Y0、 G S GS GS、 E O EO EO为输出端。
| EI | I 7 I_7 I7 | I 6 I_6 I6 | I 5 I_5 I5 | I 4 I_4 I4 | I 3 I_3 I3 | I 2 I_2 I2 | I 1 I_1 I1 | I 0 I_0 I0 | Y 2 Y_2 Y2 | Y 1 Y_1 Y1 | Y 0 Y_0 Y0 | G S GS GS | E O EO EO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | × | × | × | × | × | × | × | × | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | × | × | × | × | × | × | × | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | × | × | × | × | × | × | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | × | × | × | × | × | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | × | × | × | × | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | × | × | × | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | × | × | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | × | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
- 工作情况:
EI=0,编码器不工作。输出端均为低电平,GS和EO也为低电平。
EI=1,且所有输入端输入都为0时,EO=1,编码器可以串联。
EI=1,编码器正常工作,此时GS=1表示输入端有高电平信号输入。 - 逻辑表达式:
Y 2 = E I ( I 7 + I 6 + I 5 + I 4 ) Y_2=EI(I_7+I_6+I_5+I_4) Y2=EI(I7+I6+I5+I4)
Y 1 = E I ( I 7 + I 6 + I ‾ 5 I ‾ 4 I 3 + I ‾ 5 I ‾ 4 I 2 ) Y_1=EI(I_7+I_6+\overline I_5\overline I_4I_3+\overline I_5\overline I_4I_2) Y1=EI(I7+I6+I5I4I3+I5I4I2)
KaTeX parse error: Undefined control sequence: \overlineI at position 12: Y_0=EI(I_7+\̲o̲v̲e̲r̲l̲i̲n̲e̲I̲_6I_5+\overline…
KaTeX parse error: Undefined control sequence: \overlineI at position 7: EO=EI(\̲o̲v̲e̲r̲l̲i̲n̲e̲I̲_7\overlineI_6\…
G S = E I ( I 7 + I 6 + I 5 + I 4 + I 3 + I 2 + I 1 + I 0 ) GS=EI(I_7+I_6+I_5+I_4+I_3+I_2+I_1+I_0) GS=EI(I7+I6+I5+I4+I3+I2+I1+I0)
4-2 译码器/数据分配器
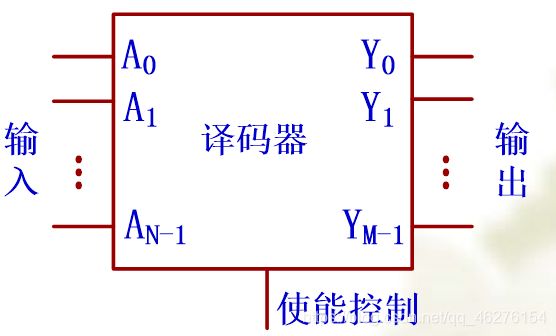
译码:编码的逆过程,把给定的二进制代码转换为相应的输出信号或另一种形式的代码。
译码器:具有译码功能的逻辑电路。
输入和输出之间要满足: M ≤ 2 N M\leq2^N M≤2N
4-2-1 二进制编码器
将输入代码转换成一一对应的有效信号,在使能控制端有效的情况下,对应每一组输入代码,输出端只有一个输出有效。
注意:输入输出满足 M = 2 N M=2^N M=2N,也称为N线-M线译码器或唯一地址译码器。
(1)2线-4线译码器
- 功能表: E ‾ \overline E E、 A 1 A_1 A1、 A 2 A_2 A2为输入, Y ‾ 3 \overline Y_3 Y3、 Y ‾ 2 \overline Y_2 Y2、 Y ‾ 1 \overline Y_1 Y1、 Y ‾ 0 \overline Y_0 Y0为输出。
| E ‾ \overline E E | A 1 A_1 A1 | A 2 A_2 A2 | Y ‾ 3 \overline Y_3 Y3 | Y ‾ 2 \overline Y_2 Y2 | Y ‾ 1 \overline Y_1 Y1 | Y ‾ 0 \overline Y_0 Y0 |
|---|---|---|---|---|---|---|
| 1 | × | × | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
- E ‾ = 0 \overline E=0 E=0译码器工作,对应每个代码仅有一个输出端有效,从而识别四种不同的输入代码。
Y ‾ 3 = A 1 A 0 ‾ = m ‾ 3 \overline Y_3=\overline{A_1A_0}=\overline m_3 Y3=A1A0=m3
Y ‾ 2 = A 1 A ‾ 0 ‾ = m ‾ 2 \overline Y_2=\overline{A_1\overline A_0}=\overline m_2 Y2=A1A0=m2
Y ‾ 1 = A ‾ 1 A 0 ‾ = m ‾ 1 \overline Y_1=\overline{\overline A_1 A_0}=\overline m_1 Y1=A1A0=m1
Y ‾ 1 = A ‾ 1 A 0 ‾ = m ‾ 0 \overline Y_1=\overline{\overline A_1 A_0}=\overline m_0 Y1=A1A0=m0
可见,译码器的输出包含了 A 1 、 A 0 A_1、A_0 A1、A0组成的所有最小项。
(1)3线-8线译码器:74HC138
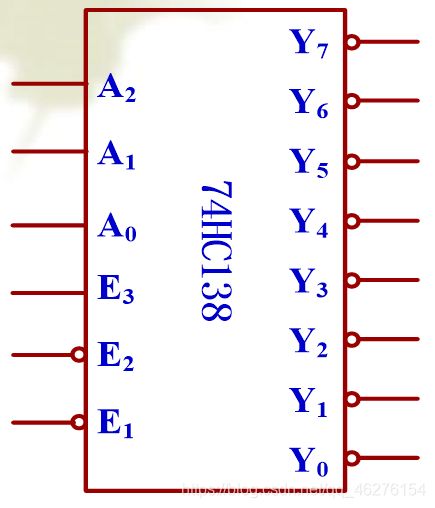
译码器有3个输入,8个反码输出,输出为低电平有效,3个使能控制端 E 3 、 E ‾ 2 、 E ‾ 1 E_3、\overline E_2、\overline E_1 E3、E2、E1。 - 功能表:
| E 3 E_3 E3 | E ‾ 2 \overline E_2 E2 | E ‾ 1 \overline E_1 E1 | A 2 A_2 A2 | A 1 A_1 A1 | A 0 A_0 A0 | Y ‾ 7 \overline Y_7 Y7 | Y ‾ 6 \overline Y_6 Y6 | Y ‾ 5 \overline Y_5 Y5 | Y ‾ 4 \overline Y_4 Y4 | Y ‾ 3 \overline Y_3 Y3 | Y ‾ 2 \overline Y_2 Y2 | Y ‾ 1 \overline Y_1 Y1 | Y ‾ 0 \overline Y_0 Y0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | × | × | × | × | × | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| × | 1 | × | × | × | × | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| × | × | 1 | × | × | × | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
4-2-2 二-十进制译码器
将输入的BCD码译成十个输出信号,有4个输入端,10个输出端,常称为4线-10线译码器。
常用的有8421BCD码集成译码器74HC42。

74HC42输出也为低电平有效,假设输入为1001时,输出端仅Y9为低电平,其他输出端为高电平,对应于十进制数9。
当输入超过0~9范围时,输出均为高电平,无有效译码输出,这超出范围的六个代码1010~1111称为伪码,显然,电路具有拒绝伪码的功能。
4-2-3 显示译码器
(1)由发光二极管构成的七段显示器(LED数码管)

a~g七个发光二极管分段封装而成,共阳极接法将各段阳极接在一起作为公共阳极接到高电平,需要某段发光,则将相应二极管的阴极接低电平,共阴极接法反之。
(2)七段集成显示译码器
将需要显示的十进制数的代码经过译码器译出送到LED数码管,点亮相应的段即可在数码管上显示十进制数。
4-2-4 数据分配器
实现数据分配的逻辑电路,将一路通道上的公共数据根据需要分配到多路通道上去,至于传送到哪路通道上,则需要用唯一地址译码器来决定。
通常数据分配器有1根输入线,n根地址控制线, 2 n 2^n 2n根数据输出线,因此根据输出线的个数也称为 2 n 2^n 2n路数据分配器。
用74HC138译码器实现的数据分配器
译码器的三个输入端A、 A1、A作为选择通道用的地址信号输入,八个输出端作为数据输出通道,三个控制端接法如下:
E ‾ 1 \overline E_1 E1接低电平; E 3 E_3 E3接高电平; E ‾ 2 \overline E_2 E2接数据线D作为数据输入。
不论D为何值,总有Y通道输出和D相同。即数据D被分配到了Y通道。

74HC138实现的数据分配器功能表
| E 3 E_3 E3 | E ‾ 2 \overline E_2 E2 | E ‾ 1 \overline E_1 E1 | A 2 A_2 A2 | A 1 A_1 A1 | A 0 A_0 A0 | Y ‾ 7 \overline Y_7 Y7 | Y ‾ 6 \overline Y_6 Y6 | Y ‾ 5 \overline Y_5 Y5 | Y ‾ 4 \overline Y_4 Y4 | Y ‾ 3 \overline Y_3 Y3 | Y ‾ 2 \overline Y_2 Y2 | Y ‾ 1 \overline Y_1 Y1 | Y ‾ 0 \overline Y_0 Y0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | D | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | D |
| 1 | D | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | D | 1 |
| 1 | D | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | D | 1 | 1 |
| 1 | D | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | D | 1 | 1 | 1 |
| 1 | D | 0 | 1 | 0 | 0 | 1 | 1 | 1 | D | 1 | 1 | 1 | 1 |
| 1 | D | 0 | 1 | 0 | 1 | 1 | 1 | D | 1 | 1 | 1 | 1 | 1 |
| 1 | D | 0 | 1 | 1 | 0 | 1 | D | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | D | 0 | 1 | 1 | 1 | D | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
4-3 数据选择器
实现数据选择功能的逻辑电路,通过选择,按需要把多个通道上的某路数据传送到唯一的公共数据通道。
一般,有 2 n 2^n 2n根输入线和一根输出线,n根选择控制线,因此根据输入线的个数也称为 2 n 2^n 2n选1数据选择器。
| 选择输入 | 输出 |
|---|---|
| 0 | D 0 D_0 D0 |
| 1 | D 1 D_1 D1 |
Y = S ‾ D 0 + S D 1 Y= \overline SD_0+SD_1 Y=SD0+SD1
| S 1 S_1 S1 | S 0 S_0 S0 | Y |
|---|---|---|
| 0 | 0 | D 0 D_0 D0 |
| 0 | 1 | D 1 D_1 D1 |
| 1 | 0 | D 2 D_2 D2 |
| 1 | 1 | D 3 D_3 D3 |
Y = S ‾ 1 S ‾ 0 D 0 + S ‾ 1 S 0 D 1 + S 1 S ‾ 0 D 2 + S 1 S 0 D 3 = m 0 D 0 + m 1 D 1 + m 2 D 2 + m 3 D 3 = ∑ i = 0 3 m i D i Y=\overline S_1\overline S_0D_0+\overline S_1S_0D_1+S_1\overline S_0D_2+ S_1S_0D_3=m_0D_0+m_1D_1+m_2D_2+m_3D_3=\sum_{i=0}^3m_iD_i Y=S1S0D0+S1S0D1+S1S0D2+S1S0D3=m0D0+m1D1+m2D2+m3D3=i=0∑3miDi
- 数据选择器又称为多路复用器,数据分配器又称为多路分配器,可以用于通信系统中的信号传输。
常用的八选一集成数据选择器74HC151:

A 2 、 A 1 、 A 0 A_2、A_1、 A_0 A2、A1、A0三位地址输入端,可实现八个数据源 D 0 ~ D 7 D_0~D_7 D0~D7的选择。
输出端Y为同相输出; Y ‾ \overline Y Y为反相输出;
E ‾ \overline E E为片选信号,低电平有效。
功能表:
| E ‾ \overline E E | A 2 A_2 A2 | A 1 A_1 A1 | A 0 A_0 A0 | Y Y Y | Y ‾ \overline Y Y |
|---|---|---|---|---|---|
| 1 | × | × | × | 0 | 1 |
| 0 | 0 | 0 | 0 | D 0 D_0 D0 | D ‾ 0 \overline D_0 D0 |
| 0 | 0 | 0 | 1 | D 1 D_1 D1 | D ‾ 1 \overline D_1 D1 |
| 0 | 0 | 1 | 0 | D 2 D_2 D2 | D ‾ 2 \overline D_2 D2 |
| 0 | 0 | 1 | 1 | D 3 D_3 D3 | D ‾ 3 \overline D_3 D3 |
| 0 | 1 | 0 | 0 | D 4 D_4 D4 | D ‾ 4 \overline D_4 D4 |
| 0 | 1 | 0 | 1 | D 5 D_5 D5 | D ‾ 5 \overline D_5 D5 |
| 0 | 1 | 1 | 0 | D 6 D_6 D6 | D ‾ 6 \overline D_6 D6 |
| 0 | 1 | 1 | 1 | D 7 D_7 D7 | D ‾ 7 \overline D_7 D7 |
4-4 数值比较器
4-4-1 一位数值比较器
实现两个一位二进制数数值比较的逻辑电路。
输入变量:A、B
输出变量: F A > B F_{A>B} FA>B、 F A < B F_{A
4-4-2 多位数值比较器
4-5 算数运算电路
4-5-1 半加器和全加器
- 半加:在做二进制加法运算时只考虑两个加数本身,而不考虑低位有无进位。
- 半加器:实现半加运算的逻辑电路。
A、B为两个1位二进制加数,S为两数的和,C为向高位产生的进位。
真值表:
| A | B | S | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
逻辑表达式为: S = A ‾ B + A B ‾ = A ⊕ B S=\overline AB+A\overline B=A\oplus B S=AB+AB=A⊕B
C = A B C=AB C=AB

- 全加:不仅考虑两个加数本身,还考虑来自相邻低位的进位,并根据求和结果给出向高位的进位信号。
- 全加器:实现全加运算的逻辑电路。
真值表:
| A | B | C i C_i Ci | S | C 0 C_0 C0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
由真值表可得全加器的逻辑表达式:
S = A ⊕ B ⊕ C i S=A\oplus B\oplus C_i S=A⊕B⊕Ci
C 0 = A B + ( A ⊕ B ) C i C_0=AB+(A\oplus B) C_i C0=AB+(A⊕B)Ci

4-5-2 多位数加法器
将多个全加器串行进位的方法就可组成多位数加法器。
特点:电路简单,但速度较慢。