《深入理解计算机系统》（CSAPP）实验六 —— Cache Lab

这是CSAPP的第6个实验，本实验将帮助我们了解缓存对C语言性能的影响。而且，这个实验比前几个难度都加大了，做实验前建议先去看24张图7000字详解计算机中的高速缓存，理解下Cache的基本原理。

1. 实验目的

  本次实验室由两部分组成。第一部分是要模拟Cahce的行为，理解Cache的原理。第二部分将优化一个小的矩阵转置功能，目的是最大程度地减少高速缓存未命中的次数。

2. 实验准备

  实验用到的所有文件在CSAPP官网都可以找到。我的运行环境Ubuntu 16.04，Gcc 5.4.0。

2.1 参考跟踪文件

  讲义目录的traces子目录包含参考跟踪文件的集合，我们将使用这些参考跟踪文件来评估在A部分中编写的缓存模拟器的正确性。跟踪文件由名为valgrind的Linux程序生成。例如，输入

valgrind --version # 检查有没有安装valgrind
sudo apt install valgrind # 没有安装的话执行这一步

linux> valgrind --log-fd=1 --tool=lackey -v --trace-mem=yes ls -l

  在命令行上运行可执行程序“ ls -l”，按其发生的顺序捕获其每个内存访问的跟踪，并在stdout上打印它们。

  Valgrind内存跟踪具有以下形式：

I 0400d7d4,8
M 0421c7f0,4
L 04f6b868,8
S 7ff0005c8,8

  每行表示一个或两个内存访问。每行的格式是

[space]operation address,size

  操作字段表示内存访问的类型：“ I”表示指令加载，“ L”表示数据加载，“ S”表示数据存储，“ M”表示数据修改（即数据加载后跟数据存储） 。每个“ I”之前都没有空格。每个“ M”，“ L”和“ S”之前总是有一个空格。地址字段指定64位十六进制内存地址。 size字段指定操作访问的字节数。

2.2 注意事项

1. 必须在64位x86-64计算机上运行此实验。

2. 不要让Windows WinZip程序打开.tar文件。而是将文件保存到Linux目录中，并使用Linux tar程序提取文件。

3. 我们只对数据高速缓存性能感兴趣，因此应忽略所有指令高速缓存访问（以“ I”开头的行）。

4. 要获得A部分的学分，必须在主函数末尾调用函数printSummary，其中包含命中，未命中和逐出的总数：

   printSummary(hit_count, miss_count, eviction_count);
   

   对于本实验，应该假定内存访问已正确对齐，以使单个内存访问永远不会越过块边界。通过进行此假设，您可以忽略valgrind跟踪中的请求大小。

5. csim.c文件必须在没有警告的情况下进行编译才能获得分数。

6. 编写的Cache模拟器必须对任意s，E和b正确工作。

3. PartA Cache simulator

3.1 说明

  在A部分中，我们要在csim.c中编写一个缓存模拟器，该模拟器以valgrind内存跟踪为输入，在该跟踪上模拟缓存的命中/未命中行为，并输出命中，未命中和逐出的总数。

  我们提供了参考缓存模拟器的二进制可执行文件，称为csim-ref，它可在valgrind跟踪文件上模拟具有任意大小和关联性的缓存行为。它使用LRU（最近使用）替换策略选择出需要的缓存行。

  参考模拟器采用以下命令行参数：

Usage: ./csim-ref [-hv] -s  -E  -b  -t 
-h：可选的帮助标志，用于打印使用情况信息
•-v：显示跟踪信息的可选详细标志
•-s ：设置的索引位数（S = 2s是设置的数量）
•-E ：关联性（每组行数）
•-b ：块位数（B = 2b是块大小）
•-t ：要重播的valgrind跟踪的名称

  命令行参数基于CS：APP2e教科书第597页的符号（s，E和b）。例如：

linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace
hits:4 misses:5 evictions:3

  详细模式下的相同示例：

linux> ./csim-ref -v -s 4 -E 1 -b 4 -t traces/yi.trace
L 10,1 miss
M 20,1 miss hit
L 22,1 hit
S 18,1 hit
L 110,1 miss eviction
L 210,1 miss eviction
M 12,1 miss eviction hit
hits:4 misses:5 evictions:3

防止恶意转载
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_16933601/article/details/111590671

3.2 编程

3.2.1 getopt 和fscanf的使用

  PPT中给出了getopt 和fscanf的使用例程，直接拿来用就行。

int main(int argc, char** argv){
    int opt,x,y;
    /* looping over arguments */
    while(-1 != (opt = getopt(argc, argv, “x:y:"))){
    /* determine which argument it’s processing */
    switch(opt) {
    case 'x':
    x = atoi(optarg);
    break;
    case ‘y':
    y = atoi(optarg);
    break;
    default:
    printf(“wrong argument\n");
    break;
		}
	}
}

FILE * pFile; //pointer to FILE object
pFile = fopen ("tracefile.txt",“r"); //open file for reading
char identifier;
unsigned address;
int size;
// Reading lines like " M 20,1" or "L 19,3"
while(fscanf(pFile,“ %c %x,%d”, &identifier, &address, &size)>0)
{
// Do stuff
}
fclose(pFile); //remember to close file when done

3.2.2 定义结构体

  讲义中告诉我们，不需要处理B，因此cache_line结构体中包括有效位，标记位，时间戳三个变量就够了。

typedef struct{
	int valid_bits;
	unsigned  tag;
	int stamp;
}cache_line;

3.2.3 初始化Cache

  定义一个cache[S][E]大小的二维数组(using malloc). 这样cache就模拟好了。

void init(){
	cache = (cache_line**)malloc(sizeof(cache_line*)*S);             //malloc cache[S][E]
	for(int i=0;i<S;i++)
		*(cache+i) = (cache_line*)malloc(sizeof(cache_line)*E);
	for(int i=0;i<S;i++){
		for(int j=0;j<E;j++){
			cache[i][j].valid_bits = 0;      // set all valid_bits is zero
			cache[i][j].tag = 0xffffffff;           //no address
			cache[i][j].stamp = 0;            //time is 0;		
		}	
	}
}

3.2.4 解析输入的指令

  先分析每个输入的指令应该被如何操作。如果是I，则不是数据操作，直接忽略。如果是L或者S，则需要进行一次hit-mis eviction检测，如果是M，则相当于先L再S，需要进行两次hit-miss- eviction检测。然后考虑hit-miss- eviction检测细节。

	while(fscanf(file," %c %x,%d",&operation,&address,&size)>0){
		switch(operation){
			case 'L':
				update(address);
				break;
			case 'M':
				update(address);
			case 'S':
				update(address);
				break;
		}
		time();
	}

首先需要对读取的地进有分析，读取的地址结构如下所示：

低b位表示 block偏移，本实验中不需要计算blk偏移。中间s位是 set index位，表示对那个行操作。其余t位是tag位。用于标明对应的line是否有效。我们需要对得到的地址进行如下操作，解析出t和s。

	unsigned s_address =(address>>b) & ((0xffffffff)>>(32-s));                //set`s index
	unsigned t_address = address>>(s+b);                                 //tag`s index

3.2.5 LRU策略

替换策略使用的是LRU的缓存替换策略。如果该SET存满了，我每次要找到TIMESTAMP最小的替换。为了方便，我把TIMESTAMP初始化为0，之后每个操作+1. 当TIMESTAMP = 0的时候就代表不VALID。

void time(){
	for(int i=0;i<S;i++){
		for(int j=0;j<E;j++){
			if(cache[i][j].valid_bits == 1)
				cache[i][j].stamp++;		
		}	
	}
}

	for(int i=0;i<E;i++){
		if(cache[s_address][i].stamp > max_stamp){
			max_stamp = cache[s_address][i].stamp;
			max_i = i;
		}
	}

3.2.6 更新高速缓存Cache

  cache的容量有限，当满的时候需要牺牲行（或者说驱逐某行），先遍历当前组，判断它满了没有，如何判断是否满，可以遍历所有的行，只要有一个有效位为0，（有效位的作用是说明该行是否存储了数据，通俗的理解就是是否为空）则该组未满。

//更新高速缓存cache
for(int i=0;i

3.2.7 完整代码

#include "cachelab.h"
#include 
#include 
#include 
#include 
#include 
typedef struct{
	int valid_bits;
	unsigned  tag;
	int stamp;
}cache_line;
char* filepath = NULL;
int s,E,b,S;           // s is set ,E  is line,each line have 2^b bits ,S is 2^s set
int hit=0,miss=0,eviction=0;
cache_line** cache = NULL;

void init(){
	cache = (cache_line**)malloc(sizeof(cache_line*)*S);             //malloc cache[S][E]
	for(int i=0;i<S;i++)
		*(cache+i) = (cache_line*)malloc(sizeof(cache_line)*E);
	for(int i=0;i<S;i++){
		for(int j=0;j<E;j++){
			cache[i][j].valid_bits = 0;      // set all valid_bits is zero
			cache[i][j].tag = 0xffffffff;           //no address
			cache[i][j].stamp = 0;            //time is 0;		
		}	
	}
}

void update(unsigned address){
	unsigned s_address =(address>>b) & ((0xffffffff)>>(32-s));                //set`s index
	unsigned t_address = address>>(s+b);                                 //tag`s index
	//判断tag为是否相等，是否命中
    for(int i=0;i<E;i++){
		if((*(cache+s_address)+i)->tag ==t_address){
			cache[s_address][i].stamp = 0;       //now ,this is used
			hit++;
			return;
		}
	}
    //更新高速缓存cache
	for(int i=0;i<E;i++){
		if(cache[s_address][i].valid_bits == 0){
			cache[s_address][i].tag = t_address;
			cache[s_address][i].valid_bits = 1;
			cache[s_address][i].stamp = 0;       //now ,this is load
			miss++;
			return;
		}
	}
    //暴力实现LRU策略
	int max_stamp=0;
	int max_i;
	for(int i=0;i<E;i++){
		if(cache[s_address][i].stamp > max_stamp){
			max_stamp = cache[s_address][i].stamp;
			max_i = i;
		}
	}
	eviction++;
	miss++;
	cache[s_address][max_i].tag = t_address;
	cache[s_address][max_i].stamp = 0;	
}
void time(){
	for(int i=0;i<S;i++){
		for(int j=0;j<E;j++){
			if(cache[i][j].valid_bits == 1)
				cache[i][j].stamp++;		
		}	
	}
}
int main(int argc,char *argv[])
{
	int opt;         
	while((opt = getopt(argc,argv,"s:E:b:t:")) !=-1){           //parse command line arguments
		switch(opt){
		case 's':
			s=atoi(optarg);
			break;
		case 'E':
			E=atoi(optarg);
			break;
		case 'b':
			b=atoi(optarg);
			break;
		case 't':
			filepath = optarg;
			break;
		}
	}
	S = 1<<s;
	init();
	FILE* file=fopen(filepath,"r");
	if(file == NULL){     // read trace file
		printf("Open file wrong");		
		exit(-1);
	}
	char operation;
	unsigned address;
	int size;	
	while(fscanf(file," %c %x,%d",&operation,&address,&size)>0){
		switch(operation){
			case 'L':
				update(address);
				break;
			case 'M':
				update(address);
			case 'S':
				update(address);
				break;
		}
		time();
	}
	for(int i=0;i<S;i++)                  //free cache[S][E]
		free(*(cache+i));
	free(cache);
	fclose(file);	                //close file	
    printSummary(hit,miss,eviction);
    return 0;
}

4. PartB Efficient Matrix Transpose

4.1 说明

  在B部分中，我们将在trans.c中编写一个转置函数，该函数将尽可能降低高速缓存未命中率。 设A表示矩阵，$A_{ij}$表示第i行第j列的分量。 A的转置
表示为$A^T$,其中，$A_{ij}=A_{ji}^T$。

  在trans.c中为提供了一个示例转置函数，用于计算转置N×M矩阵A并将结果存储在M×N矩阵B中：

char trans_desc[] = "Simple row-wise scan transpose";
void trans(int M, int N, int A[N][M], int B[M][N])

  示例的转置函数是正确的，但是效率很低，因为访问模式会导致相对许多缓存未命中。

  在B部分中，我们的工作是编写一个类似的函数，称为transpose_submit，该函数可最大程度地减少不同大小的矩阵之间的高速缓存未命中数：

char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]);

不要更改transpose_submit函数的描述字符串（“Transpose submission”）。自动分频器搜索此字符串，以确定要评估分数的转置函数。

4.2 注意事项

1. 代码必须在没有警告的情况下进行编译才能获得分数。

2. 每个转置函数最多可以定义12个int类型的局部变量。

3. 不允许使用long类型的任何变量或使用任何位技巧将多个以上的值存储到单个变量中来避开上一条规则。

4. 转置函数不能使用递归。

5. 如果选择使用辅助函数，则在辅助函数和顶级转置函数之间的某个时间堆栈上最多可以包含12个局部变量。例如，如果您的转置声明了8个变量，然后调用了一个使用4个变量的函数，然后调用了另一个使用2个变量的函数，则堆栈中将有14个变量，这将违反规则。

6. 您的转置函数可能不会修改数组A。但是，您可以对数组B的内容做任何想做的事情。

7. 您不允许在代码中定义任何数组或使用malloc的任何变体。

4.3 编程

4.3.1 32 * 32 矩阵

  第一个测试矩阵大小是 32 x 32 的。我们先来分析一下，一个 int 类型数字是 4 字节，cache 中一行 32 字节，可以放 8 个 int 。先用原来给的示例代码看一下 miss 数量。

  其实这个题目和之前的Perfom Lab有点像，想要降低不命中次数，需要提高函数的局部性，要么通过修改循环顺序来提高空间局部性，要么通过分块技术来提高时间局部性。

  从空间局部性来看，矩阵A的步长为1，所以空间局部性良好，而矩阵B的步长为N，空间局部性较差，并且无论我们怎么调整循环顺序，都无法改变，所以无法从空间局部性的角度来减少不命中次数。

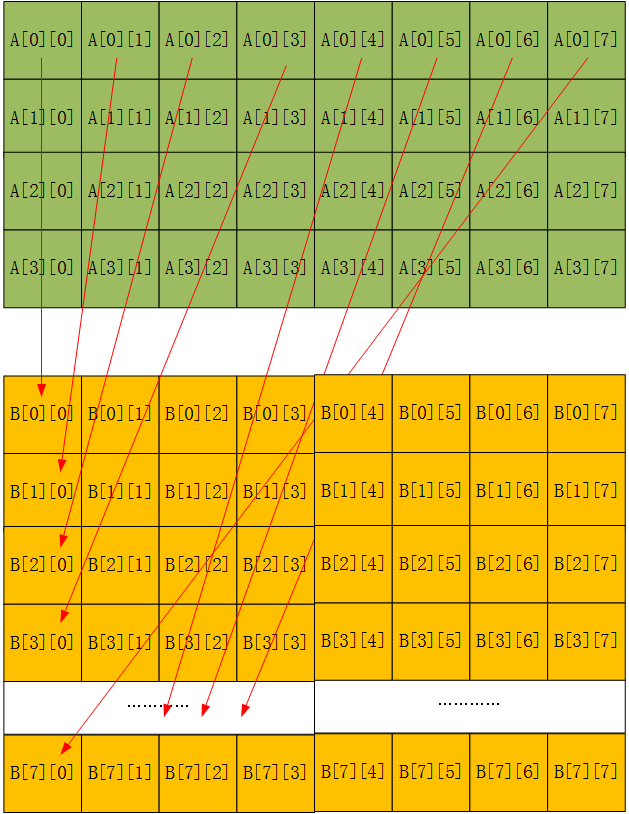
  所以我们需要通过分块技术来优化时间局部性。题目已经给定了 cache 的参数 s = 5，b = 5 ，E = 1。那么 cache 的大小就是 32 组，每组 1 行， 每行可存储 32 字节的数据。而int类型为4字节，所以缓存中的每个数据块可以保存8个元素，由于矩阵是行优先存储的，所以相当于保存了A [0] [0]~A [0] [7]，A矩阵转置后A [0] [0]~A [0] [7]对应的位置为B[0] [0]~B[7] [0]，意味着需要8个高速缓存行（B也是行优先访问），分别保存B[0] [0]~B[0] [7]、B[1] [0]~B[1] [7]……。只有这样，每次取出一个Cache，才能得到充分的利用。

  由于32x32矩阵中，每一行有32个元素，则相邻两行间隔了3个高速缓存行，比如根据矩阵B的地址，其元素保存在高速缓存中是如下形式。

组号	元素
0	B[0] [0] ~B[0] [7]
1	B[0] [8] ~B[0] [15]
2	B[0] [16] ~B[0] [23]
3	B[0] [24] ~B[0] [31]
4	B[1] [0] ~B[1] [7]
…	…

  可以发现，我们想要的B[0] [0]~B[0] [7]和B[1] [0]~B[1] [7]之间还间隔了3个高速缓存行。而该高速缓存配置刚好能保存8行（每行8个int元素，32字节），所以我们设置分块技术的块大小为8，此时高速缓存中就保存了B[0] [0]~B[0] [7]到B[7] [0]~B[7] [7]的块，则在内侧的循环中，就能充分利用这些块后才会将其丢弃，减少了原始代码中由于缓存空间有限，而驱逐了后面要用的块。

if (M == 32 && N == 32)
	{
		int i, j, m, n;
		for (i = 0; i < N; i += 8)
			for (j = 0; j < M; j += 8)
				for (m = i; m < i + 8; ++m)
					for (n = j; n < j + 8; ++n)
					{
						B[n][m] = A[m][n];
					}
	}

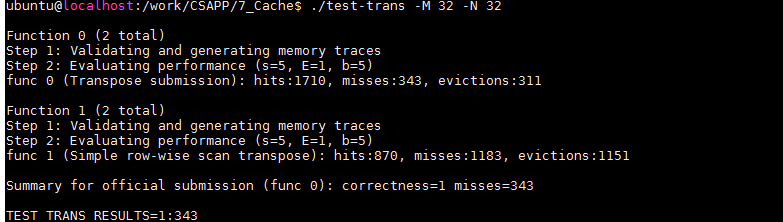
  运行下看下结果。降低到了 343 次，分块技术效果不错，但是距离满分还有一些差距。

  可以发现，A 和 B 中相同位置的元素是映射在同一 cache line 上的，但是因为我们做转置的话，并不会把 A 中某位置的元素放到 B 中相同的地方，除非在对角线上，因为下标是一样的，此时就会发生原地转置。譬如我们已经把 A 的第四行存进去了，但是当要写 B44 时，发生了冲突，第四行被换成 B 的，然后读 A 的时候又换成了 A 的，就多造成了两次 miss。

  这个时候可以使用一个简单的办法，因为除了循环需要的 4 个变量外我们还剩余 8 个自由变量可以用，正好可以存一个 cache line。以空间换时间，把一行一次性读完，减少冲突不命中。代码如下

if(M == 32 && N == 32)
	{
		int i, j, k, v1, v2, v3, v4, v5, v6, v7, v8;
		for (i = 0; i < 32; i += 8)
			for(j = 0; j < 32; j += 8)
				for(k = i; k < (i + 8); ++k)
				{
					v1 = A[k][j];
					v2 = A[k][j+1];
					v3 = A[k][j+2];
					v4 = A[k][j+3];
					v5 = A[k][j+4];
					v6 = A[k][j+5];
					v7 = A[k][j+6];			
					v8 = A[k][j+7];
					B[j][k] = v1;
					B[j+1][k] = v2;
					B[j+2][k] = v3;
					B[j+3][k] = v4;
					B[j+4][k] = v5;
					B[j+5][k] = v6;
					B[j+6][k] = v7;
					B[j+7][k] = v8;
				}
	}

4.3.2 64 * 64矩阵

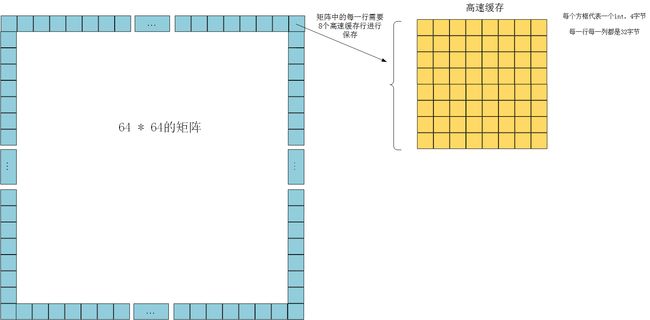
  这里同样使用分块技术进行优化，需要注意的是，当矩阵大小变为64x64时，矩阵中的每一行需要8个高速缓存行进行保存，使得高速缓存中只能保存4行的矩阵内容，如果我们还是使用块大小为8的分块技术，就会使得第5行和第1行冲突、第6行和第2行冲突等等，由此就会出现冲突不命中，所以我们只能设置块大小为4。

else if (M == 64 && N == 64)
	{
		int i, j, x, y;
		int x1, x2, x3, x4, x5, x6, x7, x8;
		for (i = 0; i < N; i += 8)
			for (j = 0; j < M; j += 8)
			{
				for (x = i; x < i + 4; ++x)
				{
					x1 = A[x][j]; x2 = A[x][j+1]; x3 = A[x][j+2]; x4 = A[x][j+3];
					x5 = A[x][j+4]; x6 = A[x][j+5]; x7 = A[x][j+6]; x8 = A[x][j+7];
					
					B[j][x] = x1; B[j+1][x] = x2; B[j+2][x] = x3; B[j+3][x] = x4;
					B[j][x+4] = x5; B[j+1][x+4] = x6; B[j+2][x+4] = x7; B[j+3][x+4] = x8;
				}
				for (y = j; y < j + 4; ++y)
				{
					x1 = A[i+4][y]; x2 = A[i+5][y]; x3 = A[i+6][y]; x4 = A[i+7][y];
					x5 = B[y][i+4]; x6 = B[y][i+5]; x7 = B[y][i+6]; x8 = B[y][i+7];
					
					B[y][i+4] = x1; B[y][i+5] = x2; B[y][i+6] = x3; B[y][i+7] = x4;
					B[y+4][i] = x5; B[y+4][i+1] = x6; B[y+4][i+2] = x7; B[y+4][i+3] = x8;
				}
				for (x = i + 4; x < i + 8; ++x)
				{
					x1 = A[x][j+4]; x2 = A[x][j+5]; x3 = A[x][j+6]; x4 = A[x][j+7];
					B[j+4][x] = x1; B[j+5][x] = x2; B[j+6][x] = x3; B[j+7][x] = x4;
				}
			}
	}

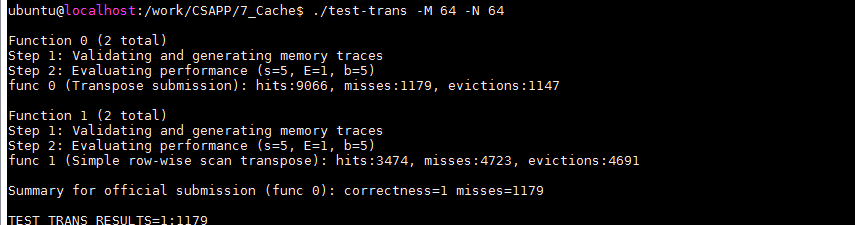
  比如我们使用块大小为8，则不命中数目为4723，当修改块大小为4时，不命中次数为1179。

4.3.3 61 * 67矩阵

  这个相对 64 来说好想一点，因为不是正好的边边相等的矩形，所以不一定要用 8 分块，一个个试下来发现单纯分块的话，17 分块达到了最小的是 1950 次。但是这样很粗糙，我们还是用 8 分块去稍微对对角线做下操作，因为 32 x 32 最小的 miss 的方法和这边是一样的，而且写起来太多了，我们就用最简单的存变量的方式去做。

else if(M == 61 && N == 67)
	{
		int i, j, v1, v2, v3, v4, v5, v6, v7, v8;
		int n = N / 8 * 8;
		int m = M / 8 * 8;
		for (j = 0; j < m; j += 8)
			for (i = 0; i < n; ++i)
			{
				v1 = A[i][j];
				v2 = A[i][j+1];
				v3 = A[i][j+2];
				v4 = A[i][j+3];
				v5 = A[i][j+4];
				v6 = A[i][j+5];
				v7 = A[i][j+6];
				v8 = A[i][j+7];
				
				B[j][i] = v1;
				B[j+1][i] = v2;
				B[j+2][i] = v3;
				B[j+3][i] = v4;
				B[j+4][i] = v5;
				B[j+5][i] = v6;
				B[j+6][i] = v7;
				B[j+7][i] = v8;
			}
		for (i = n; i < N; ++i)
			for (j = m; j < M; ++j)
			{
				v1 = A[i][j];
				B[j][i] = v1;
			}
		for (i = 0; i < N; ++i)
			for (j = m; j < M; ++j)
			{
				v1 = A[i][j];
				B[j][i] = v1;
			}
		for (i = n; i < N; ++i)
			for (j = 0; j < M; ++j)
			{
				v1 = A[i][j];
				B[j][i] = v1;
			}
	}

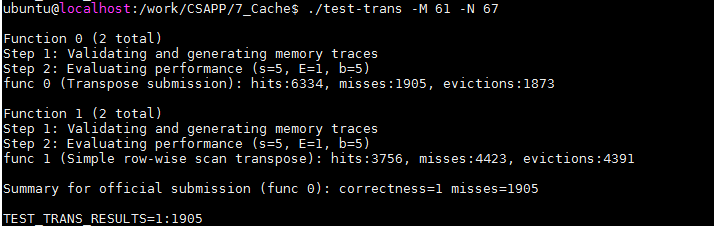
  最后结果为1905，也达到了要求。

5. 总结

  整个实验难度确实提升不少，刚开始看完书发现对Cache缓存的过程还是不理解，又回去看了下才来做题。网上也看下其他大佬写的代码。感谢以下几位大佬写的文章。

[读书笔记]CSAPP：CacheLab

CSAPP实验之cachelab

《深入理解计算机系统》配套实验4: Cache lab

《深入理解计算机系统》配套实验：Cache Lab

CS:APP配套实验4：Cache Lab笔记