Elasticsearch:实用 BM25 - 第 2 部分:BM25 算法及其变量
![]()
BM25算法
我将尽可能深入这里的数学以解释正在发生的事情,但这是我们查看 BM25 公式的结构以深入了解正在发生的事情的部分。 首先我们来看看公式,然后我将把每个组件分解成可以理解的部分:
我们可以看到一些常见的组件,如 qi、IDF(qi)、f(qi,D)、k1、b,以及一些关于字段长度的内容。 这是每一个的全部内容:
1)qi 是第 i 个查询词。
例如,如果我搜索 “shane”,只有 1 个查询词,所以 q0 是 “shane”。 如果我用英文搜索 “shane connelly”,Elasticsearch 会看到空格并将其标记为 2 个术语:q0 将是 “shane”,q1 将是 connelly”。 这些查询项被插入等式的其他位,所有的都被加起来。
2)IDF(qi) 是第 i 个查询词的逆文档频率( inverse document frequency)。
对于以前使用过 TF/IDF 的人来说,IDF 的概念对你来说可能很熟悉。 如果没有,不用担心! (如果是这样,请注意 TF/IDF 中的 IDF 公式与 BM25 中的 IDF 之间存在差异。)我们公式的 IDF 组件衡量一个术语在所有文档中出现的频率,并 “惩罚” 常见的术语。 这部分 Lucene/BM25 使用的实际公式是:
其中 docCount 是分片中具有该字段值的文档总数(跨分片,如果你使用 search_type=dfs_query_then_fetch),f(qi) 是包含第 i 个查询词的文档数。 我们可以在示例中看到 “shane” 出现在所有 4 个文档中,因此对于术语 “shane”,我们最终得到一个 IDF(“shane”):
然而,我们可以看到 “connelly” 只出现在 2 个文档中,所以我们得到一个 IDF(“connelly”):
我们可以在这里看到包含这些较稀有术语的查询(“connelly” 在我们的 4 文档语料库中比 “shane” 更稀有)具有更高的乘数,因此它们对最终分数的贡献更大。 这符合直觉:术语 “the” 可能出现在几乎所有英文文档中,因此当用户搜索 “the elephant” 之类的内容时,“elephant” 可能更重要 —— 我们希望它对 分数 —— 而不是术语 “the”(几乎所有文档中都会出现)。
3)我们看到分母中字段的长度除以平均字段长度为 fieldLen/avgFieldLen。
我们可以将其视为文档相对于平均文档长度的长度。 如果文档长于平均值,则分母变大(分数降低),如果文档短于平均值,则分母变小(分数增加)。 请注意,Elasticsearch 中字段长度的实现是基于术语的数量(相对于字符长度等其他因素)。 这与原始 BM25 论文中的描述完全相同,但如果你愿意,我们确实有一个特殊标志 (discount_overlaps) 来专门处理同义词。 考虑这一点的方法是,文档中的术语越多 —— 至少是与查询不匹配的术语 —— 文档的分数越低。 同样,这具有直觉意义:如果一份文档有 300 页长,并且只提到了我的名字一次,那么它与我的关系就不太可能像一条提到我一次的短推文那样与我有关。
4)我们看到一个变量 b 出现在分母中,它乘以我们刚刚讨论的字段长度的比率。 如果 b 越大,文档长度与平均长度相比的影响就越大。 看到这一点,你可以想象如果将 b 设置为 0,则长度比率的影响将完全无效,文档的长度将不会影响分数。 默认情况下,b 在 Elasticsearch 中的值为 0.75。
5)最后,我们看到分数的两个组成部分同时出现在分子和分母中:k1 和 f(qi,D)。 它们在两侧的出现让人很难仅通过公式了解它们的作用,但让我们快速进入。
- f(qi,D) 是 “文档 D 中第 i 个查询词出现了多少次?” 在所有这些文档中,f(“shane”, D) 为 1,但 f(“connelly”, D) 有所不同:文档 3 和 4 为 1,文档 1 和 2 为 0。如果有第 5 个 有文本 “shane shane” 的文档,它的 f(“shane”,D) 为 2。我们可以看到 f(qi, D) 在分子和分母中,还有那个特殊的“ k1” 我们接下来要讨论的因素。 考虑 f(qi,D) 的方式是查询词在文档中出现的次数越多,它的分数就越高。 这在直觉上是有道理的:一份多次出现我们名字的文档比只出现一次的文档更有可能与我们相关。
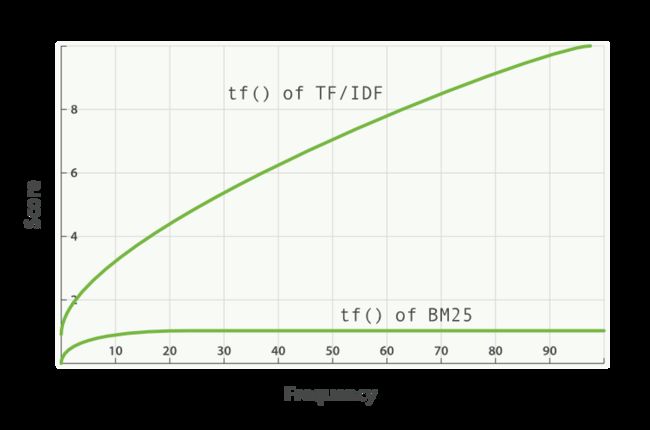
- k1 是帮助确定术语频率饱和特性的变量。 也就是说,它限制了单个查询词对给定文档分数的影响程度。 它通过接近渐近线来做到这一点。 你可以在这里看到 BM25 与 TF/IDF 的比较:
更高/更低的 k1 值意味着 “BM25 的 tf()” 曲线的斜率发生变化。 这具有改变 “术语出现额外次数增加额外分数” 的方式的效果。 对 k1 的解释是,对于平均长度的文档,术语频率的值给出的分数是所考虑术语的最大分数的一半。 tf 对分数的影响曲线在 tf() ≤ k1 时增长很快,而在 tf() > k1 时越来越慢。
继续我们的示例,对于 k1,我们控制了“向文档添加第二个 ‘shane’ 对得分的贡献比第一个或第三个与第二个相比多多少?”这个问题的答案。 较高的 k1 意味着对于该术语的更多实例,每个术语的分数可以继续上升相对更多。 k1 的值为 0 意味着除 IDF(qi) 之外的所有内容都将抵消。 默认情况下,k1 在 Elasticsearch 中的值为 1.2。
用我们的新知识重新审视我们的搜索
我们将删除我们的人员索引并仅使用 1 个分片重新创建它,这样我们就不必使用 search_type=dfs_query_then_fetch。 我们将通过设置三个索引来测试我们的知识:一个 k1 的值为 0,b 为 0.5,第二个索引 (people2) 的值为 b 为 0,k1 为 10,第三个索引 (people3) b 的值为 1,k1 为 5。
DELETE people
PUT people
{
"settings": {
"number_of_shards": 1,
"index" : {
"similarity" : {
"default" : {
"type" : "BM25",
"b": 0.5,
"k1": 0
}
}
}
}
}
PUT people2
{
"settings": {
"number_of_shards": 1,
"index" : {
"similarity" : {
"default" : {
"type" : "BM25",
"b": 0,
"k1": 10
}
}
}
}
}
PUT people3
{
"settings": {
"number_of_shards": 1,
"index" : {
"similarity" : {
"default" : {
"type" : "BM25",
"b": 1,
"k1": 5
}
}
}
}
}现在我们将向所有三个索引添加一些文档:
POST people/_doc/_bulk
{ "index": { "_id": "1" } }
{ "title": "Shane" }
{ "index": { "_id": "2" } }
{ "title": "Shane C" }
{ "index": { "_id": "3" } }
{ "title": "Shane P Connelly" }
{ "index": { "_id": "4" } }
{ "title": "Shane Connelly" }
{ "index": { "_id": "5" } }
{ "title": "Shane Shane Connelly Connelly" }
{ "index": { "_id": "6" } }
{ "title": "Shane Shane Shane Connelly Connelly Connelly" }
POST people2/_doc/_bulk
{ "index": { "_id": "1" } }
{ "title": "Shane" }
{ "index": { "_id": "2" } }
{ "title": "Shane C" }
{ "index": { "_id": "3" } }
{ "title": "Shane P Connelly" }
{ "index": { "_id": "4" } }
{ "title": "Shane Connelly" }
{ "index": { "_id": "5" } }
{ "title": "Shane Shane Connelly Connelly" }
{ "index": { "_id": "6" } }
{ "title": "Shane Shane Shane Connelly Connelly Connelly" }
POST people3/_doc/_bulk
{ "index": { "_id": "1" } }
{ "title": "Shane" }
{ "index": { "_id": "2" } }
{ "title": "Shane C" }
{ "index": { "_id": "3" } }
{ "title": "Shane P Connelly" }
{ "index": { "_id": "4" } }
{ "title": "Shane Connelly" }
{ "index": { "_id": "5" } }
{ "title": "Shane Shane Connelly Connelly" }
{ "index": { "_id": "6" } }
{ "title": "Shane Shane Shane Connelly Connelly Connelly" }现在,当我们这样做时:
GET /people/_search
{
"query": {
"match": {
"title": "shane"
}
}
}我们可以在 people 中看到所有文档的分数都是 0.074107975。 这符合我们对将 k1 设置为 0 的理解:只有搜索词的 IDF 对分数有影响!
现在让我们检查 people2,它有 b = 0 和 k1 = 10:
GET /people2/_search
{
"query": {
"match": {
"title": "shane"
}
}
}从这次搜索的结果中可以看出两点。
首先,我们可以看到分数完全按照 “shane” 出现的次数排序。 文档 1、2、3 和 4 都有一次 “shane”,因此共享相同的分数 0.074107975。 文档 5 有两次“shane”,因此由于 f(“shane”, D5) = 2 而获得更高的分数 (0.13586462),由于 f(“shane”, D6) = 3,文档 6 再次获得更高的分数 (0.18812023)。这符合我们将 people2 中的 b 设置为 0 的直觉:长度 —— 或文档中术语的总数 —— 不影响评分; 只有匹配项的计数和相关性。
第二点要注意的是,这些分数之间的差异是非线性的,尽管这 6 个文档看起来确实非常接近线性。
- 没有出现我们的搜索词和第一次出现之间的分数差异是 0.074107975
- 添加我们的搜索词的第二次出现和第一次出现之间的分数差异是 0.13586462 - 0.074107975 = 0.061756645
- 添加我们的搜索词的第三次出现和第二次出现之间的分数差异是 0.18812023 - 0.13586462 = 0.05225561
0.074107975 非常接近 0.061756645,而 0.061756645 非常接近 0.05225561,但它们明显在下降。 这看起来几乎是线性的原因是因为 k1 很大。 我们至少可以看到分数并没有随着出现次数的增加而线性增加 —— 如果是的话,我们希望看到每个额外的词项都有相同的差异。 我们将在查看 people3 后回到这个想法。
现在让我们检查 people3,它有 k1 = 5 和 b = 1:
GET /people3/_search
{
"query": {
"match": {
"title": "shane"
}
}
}我们得到以下命中:
"hits": [
{
"_index": "people3",
"_type": "_doc",
"_id": "1",
"_score": 0.16674294,
"_source": {
"title": "Shane"
}
},
{
"_index": "people3",
"_type": "_doc",
"_id": "6",
"_score": 0.10261105,
"_source": {
"title": "Shane Shane Shane Connelly Connelly Connelly"
}
},
{
"_index": "people3",
"_type": "_doc",
"_id": "2",
"_score": 0.102611035,
"_source": {
"title": "Shane C"
}
},
{
"_index": "people3",
"_type": "_doc",
"_id": "4",
"_score": 0.102611035,
"_source": {
"title": "Shane Connelly"
}
},
{
"_index": "people3",
"_type": "_doc",
"_id": "5",
"_score": 0.102611035,
"_source": {
"title": "Shane Shane Connelly Connelly"
}
},
{
"_index": "people3",
"_type": "_doc",
"_id": "3",
"_score": 0.074107975,
"_source": {
"title": "Shane P Connelly"
}
}
]我们可以在 people3 中看到,现在匹配项(“shane”)与不匹配项的比率是唯一影响相对得分的因素。 因此,像文档 3 这样的文档,在低于文档 2、4、5 和 6 的 3 个得分中只有 1 个词匹配,它们都恰好匹配了一半的词,而那些得分都低于与文档 1 完全匹配的文档。
同样,我们可以注意到 people2 和 people3 中得分最高的文档和得分较低的文档之间存在 “巨大” 差异。 这(再次)归功于 k1 的较大值。 作为额外的练习,尝试删除 people2/people3 并将它们重新设置为 k1 = 0.01 之类的值,您会发现具有较少文档之间的分数更小。 当 b = 0 且 k1 = 0.01 时:
- 没有出现我们的搜索词和第一次出现之间的分数差异是 0.074107975
- 添加我们的搜索词的第二次出现和第一次出现之间的分数差异是 0.074476674 - 0.074107975 = 0.000368699
- 添加我们的搜索词的第三次出现和第二次出现之间的分数差异是 0.07460038 - 0.074476674 = 0.000123706
因此,当 k1 = 0.01 时,我们可以看到每次额外出现的分数影响比 k1 = 5 或 k1 = 10 时下降得更快。第 4 次出现对分数的影响比第 3 次增加的少得多,依此类推。 换句话说,这些较小的 k1 值会使术语得分更快地饱和。 正如我们所料!
希望这有助于了解这些参数对各种文档集的作用。 有了这些知识,接下来我们将跳转到如何选择合适的 b 和 k1 以及 Elasticsearch 如何提供工具来理解分数和迭代你的方法。