1-9 随机算法【手写+Xmind笔记】

1 Min-Cut【手写笔记】

1.1 问题描述

1.2 解决方案

1.3 概率证明

2 赠券收集【手写笔记】

3 快排期望【手写笔记】

4 素数性质【手写笔记】

4.1 基本性质

4.2 解决方案

4.3 群论

4.4 费马小定理

4.5 Miller Rabin素性测试

5-6 力矩与偏差【手写笔记】

5.1 基础不等式

5.2 矩生成函数

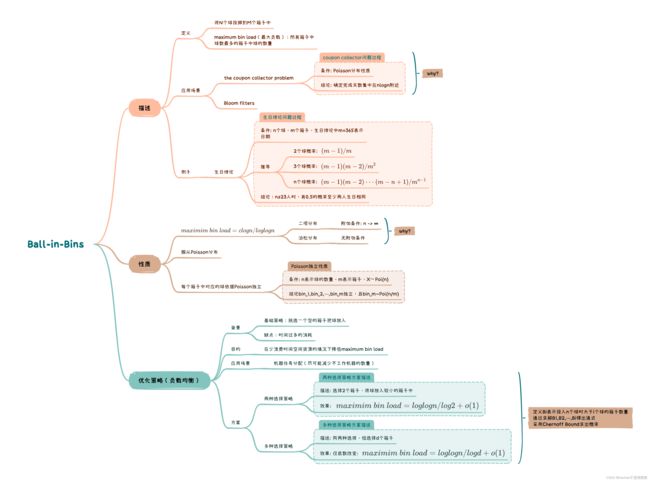
7 Ball-in-Bins问题【Xmind笔记】

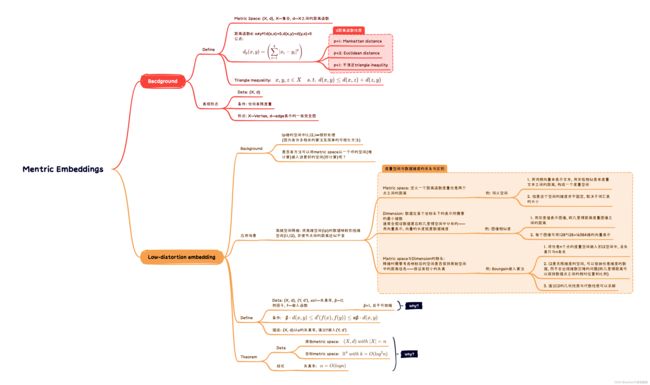
8 Mentric Embeddings【Xmind笔记】

9 降维/最近邻搜索【Xmind笔记】

9.1 JL引理

JL引理通俗的理解是：

• 存储$N$个向量，只需要最多$O(\log n)$维的空间

JL引理的优点是什么：

• 使检索成本降低，同时检索效果保持近似不变

主要实现方法：

• 随机线性投影

9.2 JL引理的背景

9.2.1 Markov’s Inequality

$$P(X\ge a)\le \frac{E[x]}{a}$$

9.2.2 Chebyshev’s Inequality

$$P(|X-E[X]|\ge a)\le \frac{Var[x]}{a^2}$$

9.2.3 Cramér Chernoff方法

• $$\forall \lambda >0\to x\ge a⟺\lambda x\ge \lambda a⟺e^{\lambda x}\ge e^{\lambda a}$$

  若运用在Markov’s Inequality中可得：
  $$P(X\ge a)=P(e^{\lambda X}\ge e^{\lambda a})\le e^{-\lambda a}E[e^{\lambda x}]$$
  既然对于任何$\lambda$都成立，那么为了提高不等式精度，可得：
  $$P(X\ge a)\le \underset{\lambda \ge 0}{\min }{e}^{-\lambda a}E[e^{\lambda x}]$$

9.2.4 单位模引理

• 设$u\in {\mathbb{R}}^n$是独立重复采样自$N(0,1/n)$的向量，$\epsilon \in (0,1)$​是给定常数，那么有：
  $$P(|{\Vert u\Vert }^2-1|\ge \epsilon )\le 2\cdot e^{-n{\epsilon }^2/8}$$
  该引理说明，当n增大时$P({\Vert u\Vert }^2-1\ge \epsilon )$概率以指数形式下降，同时$P({\Vert u\Vert }^2-1\ge \epsilon )$表示$u$向量偏离$1$的概率。所以当$n$足够大时，$N(0,1/n)$采样出的$n$维向量会非常接近单位向量

单位模引理证明：

若要证明${|\Vert u\Vert }^2-1|\ge \epsilon$，则要证明${\Vert u\Vert }^2-1\ge \epsilon$和${1-\Vert u\Vert }^2\ge \epsilon$两种情况下的概率

首先推导${\Vert u\Vert }^2-1\ge \epsilon$的概率：

• 根据Chernoff方法，可以得到：
  $$P({\Vert u\Vert }^2-1\ge \epsilon )\le \underset{\lambda >0}{\min }{e}^{-\lambda \epsilon }E\left[e^{\lambda ({\Vert u\Vert }^2-1)}\right]=\underset{\lambda >0}{\min }{e}^{-\lambda (\epsilon +1)}E\left[e^{\lambda {\Vert u\Vert }^2}\right]$$

• 若将$u$写成分量的形式$(u_1,u_2,\dots ,u_n)$，有：
  $$E\left[e^{\lambda {\Vert u\Vert }^2}\right]=E\left[e^{\lambda {\sum }_i{u}_i^2}\right]=E\left[\prod _i{e}^{\lambda u_i^2}\right]=\prod _{i}E\left[e^{\lambda u_i^2}\right]$$
  其中有（过程我也不会）：
  $$E\left[e^{\lambda u_i^2}\right]={\int }_{\infty }^{\infty }\frac{1}{\sqrt{2\pi }}{e}^{-u_i^2/2}{e}^{\lambda u_i^2/n}\mathrm{d}{u}_i=\sqrt{\frac{n}{n-2\lambda }}$$

• 根据以上可得：
  $$E\left[e^{\lambda {\Vert u\Vert }^2}\right]=\prod _i\sqrt{\frac{n}{(n-2\lambda )}}={\left(\frac{n}{n-2\lambda }\right)}^{n/2}$$

  $$P({\Vert u\Vert }^2-1\ge \epsilon )\le \underset{\lambda >0}{\min }{e}^{-\lambda (\epsilon +1)}{\left(\frac{n}{n-2\lambda }\right)}^{n/2}$$

• 右端的极小值在$\lambda =\frac{n\epsilon }{2(1+\epsilon )}$时取到（这个过程我也不会），代入可得（也不会）：
  $$P({\Vert u\Vert }^2-1\ge \epsilon )\le e^{n(\log (1+\epsilon )-\epsilon )/2}\le e^{-n{\epsilon }^2/8}$$

• （数学不好真是太悲惨了）

然后是推导$1-{\Vert u\Vert }^2\ge \epsilon$的概率：

• 同上方法，可在最后得出：
  $$P({\Vert u\Vert }^2-1\ge \epsilon )\le e^{n(\log (1-\epsilon )+\epsilon )/2}\le e^{-n{\epsilon }^2/8}$$
  因为可证$\log (1-\epsilon )+\epsilon \le \log (1+\epsilon )-\epsilon$，所以证明可沿用之前的。

因为${|\Vert u\Vert }^2-1|\ge \epsilon$包含了两部分的概率，所以相加即可得到：
$$P(|{\Vert u\Vert }^2-1|\ge \epsilon )\le 2\cdot e^{-n{\epsilon }^2/8}$$

9.2.5 正交性引理：

• 假设$u,v\in {\mathbb{R}}^n$是独立重复采样自$N(0,1/N)$的两个向量，$\epsilon \in (0,1)$是给定常数，那么有：
  $$P(|⟨u,v⟩|\ge \epsilon )\le 4e^{-n{\epsilon }^2/8}$$
  该引理说明，当$n$足够大时，任意$u$，$v$间大内积偏离$0$的概率非常小，换句话说，就是从$N(0,1/N)$中取出的两个$n$维向量接近正交。

正交性引理证明：

同样将$|⟨u,v⟩|$分为$⟨u,v⟩$与$-⟨u,v⟩$

推导$⟨u,v⟩$的概率：

• 为了套用单位模引理，我们发现$\Vert \frac{u+v}{\sqrt{2}}\Vert -1\ge \epsilon$和$1-\Vert \frac{u+v}{\sqrt{2}}\Vert \ge \epsilon$的和是$⟨u,v⟩\ge \epsilon$，所以可得：
  $$\begin{array}{rl}P(⟨u,v⟩)& \le P\left(\Vert \frac{u+v}{\sqrt{2}}\Vert -1\ge \epsilon \right)+P\left(1-\Vert \frac{u+v}{\sqrt{2}}\Vert \ge \epsilon \right)\\ & \le e^{-n{\epsilon }^2/8}+e^{-n{\epsilon }^2/8}=2e^{-n{\epsilon }^2/8}\end{array}$$

同理可推导$-⟨u,v⟩$的概率为$P(-⟨u,v⟩)=2e^{-n{\epsilon }^2/8}$

所以在结合之后可得：
$$P(|⟨u,v⟩|\ge \epsilon )\le 4e^{-n{\epsilon }^2/8}$$

9.3 JL引理推导

9.3.1 数学上的JL引理

JL引理：

• 给定$N$个向量$v_1,v_2,\dots ,v_N\in {\mathbb{R}}^m$。

• 存在变量$n>\frac{24\log N}{{\epsilon }^2}$，并且随机矩阵$A\in {\mathbb{R}}^{n\times m}$独立重复采样自$N(0,1/n)$，$\epsilon \in (0,1)$是给定的常数。

• 那么至少有$\frac{N-1}{N}$的概率，使得对于$i\ne j$时成立：
  $$(1-\epsilon ){\Vert v_i-v_j\Vert }^2\le {\Vert A{v}_i-A{v}_j\Vert }^2\le (1+\epsilon ){\Vert v_i-v_j\Vert }^2$$

引理说明了：

1. 无论向量维数$m$是多少，N个向量都可以放进$n>\frac{24\log N}{{\epsilon }^2}$维的空间中，使得他们的相对距离偏移不超过$\epsilon$
2. 降维的方法是通过采样一个随机矩阵$A$，通过$v\to Av$的变换，就有$\frac{N-1}{N}$的概率达到目的

JL引理证明：

1. $A\in {\mathbb{R}}^{n\times m}$独立重复采样自$N(0,1/n)$

2. 假设$u\in {\mathbb{R}}^m$是一个给定的单位向量，$Au$的每个分量独立服从于$N(0,1/n)$，相当于$Au$就是从$N(0,1/n)$中采样出来的$n$维向量

浅证明一下：

${(Au)}_i={\sum }_j{A}_{i,j}{u}_j$，因为$A_{i,j}$独立且为正态分布，所以${(Au)}_i$也独立也服从正态分布

均值为${\sum }_j{u}_j\times 0=0$，方差为${\sum }_j{u}_j^2\times \frac{1}{n}=\frac{1}{n}$

3. 假定$u=\frac{v_i-v_j}{\Vert v_i-v_j\Vert }$，利用单位模引理有：
   P ( ∣ ∥ A v i − v j ∥ v i − v j ∥ ∥ 2 − 1 ∣ ≥ ε ) ≤ 2 ⋅ e − n ε 2 / 8 P\left( \left\lvert {\left\lVert A \frac{v_i - v_j}{\lVert v_i - v_j \rVert} \right\rVert}^2 - 1 \right\rvert \geq \varepsilon \right) \leq 2 \cdot e^{ - n\varepsilon^2/8} P( ​ ​A∥vi​−vj​∥vi​−vj​​ ​2−1 ​≥ε)≤2⋅e−nε2/8

4. 因为要对所有$i\ne j$的组合都成立，我们求至少有一项$\ge \epsilon$的概率不超过：
   P ( ∃ ( i , j ) : ∣ ∥ A v i − v j ∥ v i − v j ∥ ∥ 2 − 1 ∣ ≥ ε ) ≤ 2 ⋅ e − n ε 2 / 8 ⋅ C N 2 P\left( \exists(i, j): \left\lvert {\left\lVert A \frac{v_i - v_j}{\lVert v_i - v_j \rVert} \right\rVert}^2 - 1 \right\rvert \geq \varepsilon \right) \leq 2 \cdot e^{ - n\varepsilon^2/8} \cdot C_N^2 P(∃(i,j): ​ ​A∥vi​−vj​∥vi​−vj​​ ​2−1 ​≥ε)≤2⋅e−nε2/8⋅CN2​

5. 上面求出了至少一项的概率，与之相反，在 ∣ ∥ A v i − v j ∥ v i − v j ∥ ∥ 2 − 1 ∣ ≤ ε \left\lvert {\left\lVert A \frac{v_i - v_j}{\lVert v_i - v_j \rVert} \right\rVert}^2 - 1 \right\rvert \leq \varepsilon ​ ​A∥vi​−vj​∥vi​−vj​​ ​2−1 ​≤ε​的条件下，一项都没有的概率就是：
   $$1-2\cdot e^{-n{\epsilon }^2/8}\cdot C_N^2=1-N\cdot (N-1)\cdot e^{-n{\epsilon }^2/8}$$

6. 若代入$n>\frac{24\log N}{{\epsilon }^2}$的条件，可以得到，在 ∣ ∥ A v i − v j ∥ v i − v j ∥ ∥ 2 − 1 ∣ ≤ ε \left\lvert {\left\lVert A \frac{v_i - v_j}{\lVert v_i - v_j \rVert} \right\rVert}^2 - 1 \right\rvert \leq \varepsilon ​ ​A∥vi​−vj​∥vi​−vj​​ ​2−1 ​≤ε的条件下，一项都没有的概率是：
   $$1-N\cdot (N-1)\cdot e^{-n{\epsilon }^2/8}\ge 1-N(N-1)N^{-3}\ge 1-N^{-1}$$

根据第6步求解出的结果就可以得到：

• 在$n>\frac{24\log N}{{\epsilon }^2}$的条件下

• 实现 ∣ ∥ A v i − v j ∥ v i − v j ∥ ∥ 2 − 1 ∣ ≤ ε \left\lvert {\left\lVert A \frac{v_i - v_j}{\lVert v_i - v_j \rVert} \right\rVert}^2 - 1 \right\rvert \leq \varepsilon ​ ​A∥vi​−vj​∥vi​−vj​​ ​2−1 ​≤ε的条件，任意两项偏移不超过$\epsilon$的概率为$1-N^{-1}$

• 而 ∣ ∥ A v i − v j ∥ v i − v j ∥ ∥ 2 − 1 ∣ ≤ ε \left\lvert {\left\lVert A \frac{v_i - v_j}{\lVert v_i - v_j \rVert} \right\rVert}^2 - 1 \right\rvert \leq \varepsilon ​ ​A∥vi​−vj​∥vi​−vj​​ ​2−1 ​≤ε的条件就是定理中的：
  $$(1-\epsilon ){\Vert v_i-v_j\Vert }^2\le {\Vert A{v}_i-A{v}_j\Vert }^2\le (1+\epsilon ){\Vert v_i-v_j\Vert }^2$$

9.3.2 内积版的JL引理

JL引理（内积版）：

• 给定$N$个单位向量$v_1,v_2,\dots ,v_N\in {\mathbb{R}}^m$。

• 存在变量$n>\frac{24\log N}{{\epsilon }^2}$，并且随机矩阵$A\in {\mathbb{R}}^{n\times m}$独立重复采样自$N(0,1/n)$，$\epsilon \in (0,1)$是给定的常数。

• 那么至少有$\frac{N-2}{N}$的概率，使得对于$i\ne j$时成立：
  $$|⟨A{v}_i,A{v}_j⟩-⟨v_i,v_j⟩|\le \epsilon$$

内积版证明：形同正交性引理的证明

通过JL引理的证明我们已知：
$$\begin{array}{rl}(1-\epsilon ){\Vert v_i-v_j\Vert }^2\le {\Vert A{v}_i-A{v}_j\Vert }^2\le (1+\epsilon ){\Vert v_i-v_j\Vert }^2& \\ (1-\epsilon ){\Vert v_i+v_j\Vert }^2\le {\Vert A{v}_i+A{v}_j\Vert }^2\le (1+\epsilon ){\Vert v_i-v_j\Vert }^2& \end{array}\text{\hspace{1em}(1)(2)}$$
已知在正交条件下$⟨a,b⟩=ab$，用$(2)-(1)$​可得：

$$4⟨v_i,v_j⟩-2\epsilon ({\Vert v_i\Vert }^2+{\Vert v_j\Vert }^2)\le 4⟨A{v}_i,A{v}_j⟩\le 4⟨v_i,v_j⟩+2\epsilon ({\Vert v_i\Vert }^2+{\Vert v_j\Vert }^2)$$

由于已知$v_i$，$v_j$都是单位向量，所以上式等价于：

$$4⟨v_i,v_j⟩-2\epsilon \cdot 2\le 4⟨A{v}_i,A{v}_j⟩\le 4⟨v_i,v_j⟩+2\epsilon \cdot 2$$

经过变换可以写成：

$$-\epsilon \le ⟨A{v}_i,A{v}_j⟩-⟨v_i,v_j⟩\le \epsilon ⟹|⟨A{v}_i,A{v}_j⟩-⟨v_i,v_j⟩|\le \epsilon$$