模拟退火+粒子群算法寻找最小值点

原理简述

1 模拟退火

和最简单的爬山法相比，模拟退火多了一个选择更差的解的概率，假设当前寻找到的解是$x_{org}$，迭代一轮找到的新解为$x_{new}$，适应度(简单问题中就是函数值)分别为$f(x_{org}),f(x_{new})$,如果新解的适应度比原来的适应度小，那么直接进行更新，进入下一轮迭代，否则以一定概率P
$$P=e^{-(f(x_{org})-f(x_{new}))/T}$$
接受新解，其中$T$是当前温度，$f(x_{org})-f(x_{new})$是能量差。
之所以使用$e^{-x}$函数是因为它在(0,+∞)上的函数值在0，1之间。 能量差值越大，选取该新解的可能性就越小。

下面给出模拟退火算法代码的基本流程：
1.设定模拟退火的参数，如初始温度$T_0$，温度衰减率$\alpha$，每个温度下的迭代次数$Lk$，整体最大迭代次数max_iters
2.外层循环max_iters次。
3.内层循环Lk次，每次按照一定规则进行新解的产生，更新等，这个按照任务需求来。
4.将温度衰减，回到2。
5.输出最值点的信息。

Py代码

import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import seaborn as sns
import matplotlib.pyplot as plt
import random

def f(x):
    return 11*np.sin(x)+7*np.cos(5*x)

#模拟退火的初始值
narvs = 1 #变量个数
T0 = 100  # 初始温度
T = T0 # 迭代中温度会发生改变，第一次迭代时温度就是T0
maxgen = 200  # 最大迭代次数
Lk = 100  # 每个温度下的迭代次数
alfa = 0.95  # 温度衰减系数
x_lb = np.array([-3]) # x的下界
x_ub = np.array([3]) # x的上界
#随机生成一个初始解
x0=np.zeros(narvs)
# 生成随机解
for i in range(len(x0)):
    # 生成0~1随机数
    r = random.uniform(0, 1)
    x0[i] = x_lb + (x_ub - x_lb) * r
y0=f(x0)

max_y=y0
best_x=np.zeros(narvs)
max_y_lst=[]
maxgen = 200
plt.ion()
x = np.arange(-3, 3, 0.01)
plt.figure(figsize=(10, 10))
plt.plot(x, f(x), 'b--')
plt.scatter(x0, f(x0), color='b')
# 模拟退火过程
for iteration in range(maxgen):  # 迭代maxgen次
    for i in range(Lk):  # 每个温度下的迭代次数
        y = np.random.randn(narvs) # 每个维度的变动幅度
        z = y / sum(y ** 2) # 缩小
        x_new = x0 + z * T
        # 超出定义域
        for j in range(0, narvs):
            if x_new[j] < x_lb[j]:
                r = random.uniform(0, 1)
                x_new[j] = r * x_lb[j] + (1 - r) * x0[j]
            elif x_new[j] > x_ub[j]:
                r = random.uniform(0, 1)
                x_new[j] = r * x_ub[j] + (1 - r) * x0[j]
        x1 = x_new
        y1 = f(x1)
        if y1 > y0:  # 如果新解函数值大于当前解的函数值
            x0 = x1  # 更新当前解为新解
            y0 = y1
        else:
            # 以一定概率接受更差的解
            p = np.exp(-(y0 - y1) / T)
            r = np.random.uniform(0, 1)
            if r < p:
                x0 = x1
                y0 = y1
        if y0 > max_y:
            max_y = y0
            best_x = x0
    plt.clf()
    plt.plot(x, f(x), 'b--')
    plt.scatter(x0, f(x0), color='r')
    plt.pause(0.01)
    max_y_lst.append(*max_y)
    T = alfa * T
plt.ioff()

#模拟退火的主要流程是类似的，针对不同优化问题，找到适合的求处新解的方式即可

2.粒子群算法求解最优化问题

粒子群和模拟退火最直观的差别就是每轮中迭代的解数量不同，粒子群有$N$个解在搜索最优处，最终选取一个适应度最好的，模拟退火就是单打独斗。直观上来说，粒子群应该更可能找到全局最优。
粒子群算法可以看B站教学粒子群算法讲的十分清晰明了。

粒子群算法最关键的两个步骤就是速度和位置的更新。
$$v=v\ast w+c_1\ast (x_{indbest}-x)+c_2\ast (x_{totbest}-x)$$
其中$w$是惯性权重，$c_1,c_2$分别是个体学习因子和总体学习因子。按照迭代求解的任务需求，后期的变动应该尽可能小，才能获得稳定的输出，所以可以对这些参数进行函数化，使得越往后越小。此外，这三者的比例不同也会带来不同结果。
$$x=x+v$$

下面展示用粒子群算法求解$xsin(x)\ast cos(2x)-2xsin(3x)+3xsin(4x)$的最小值。

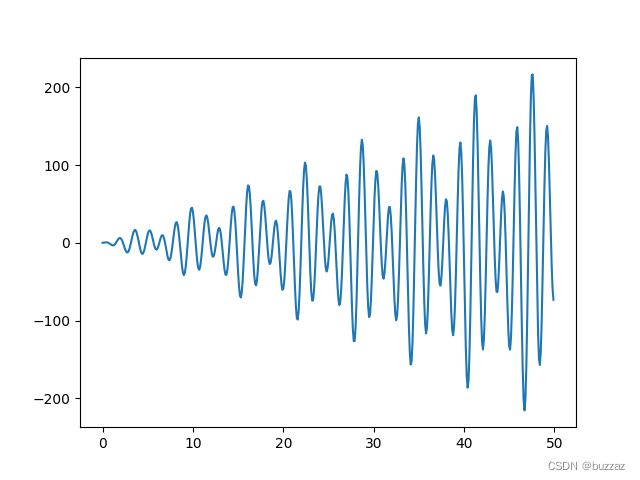
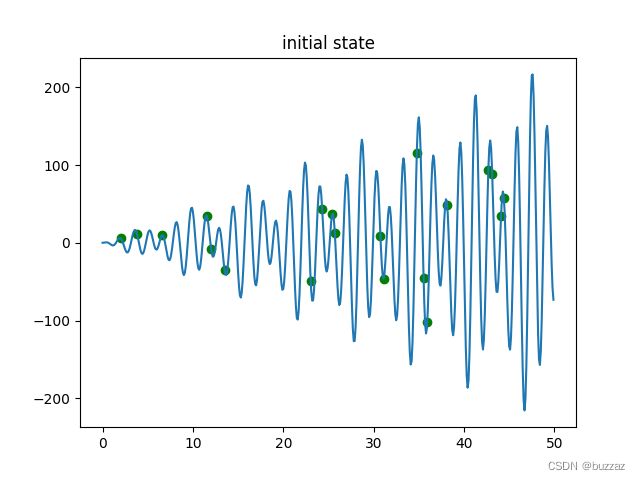
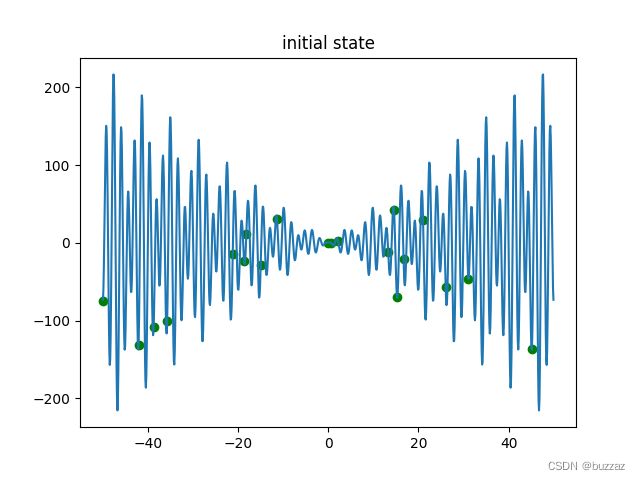
初始点的位置如下

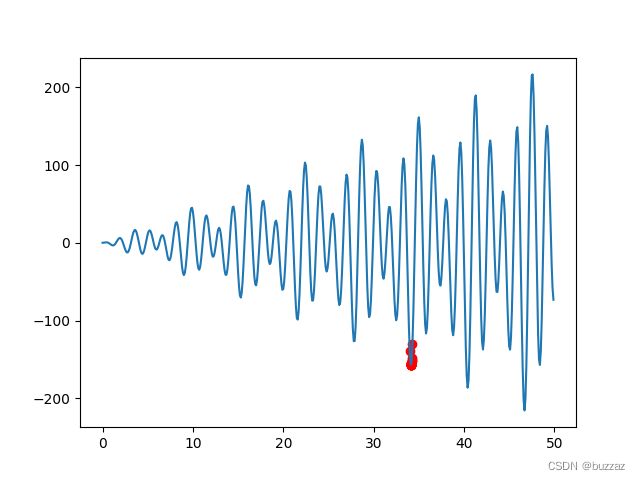
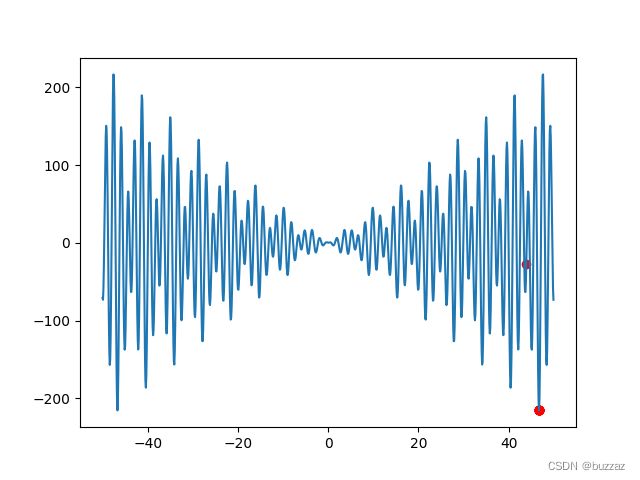
最终结果如下

寻得最小值点46.696。

不过有时候找到的是次优解。

因此我将粒子群算法写入模拟退火框架下，以一定概率选择更差的解，这样就加大了发现全局最优解的可能性。

多次运行，都能找到全局最优值，说明加上模拟退火后，算法找到全局最优的可能性大大增加。用模拟退火算法时，速度更新式中的$w,c_1,c_2$都可以像温度$T$一样，设置一个衰减率，因此它们的初始值可以设置的大一些，在初期进行比较激进的迭代。根据任务需求，三个参数的衰减率可以按照重要程度不同规定。认为总体学习重要一些的，那就将总体学习因子的衰减率设置的小一点，比如0.95.其他设置为0.9.

import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import seaborn as sns
import matplotlib.pyplot as plt
import random
import copy

#粒子群算法+模拟退火

#目标函数
def f(x):
    return x *np.sin(x) * np.cos(2 * x) - 2 * x * np.sin(3 * x) +3 * x * np.sin(4 * x)

#先实现普通的粒子群算法
def PSO_org(init,demensions,iters,tol,limit,vlimit,w,c1,c2,f):
    '''
    粒子群搜索求解(求最小值)
    :param init:初始化多少只鸟
    :param demensions: 数据维度
    :param iters: 最大迭代轮数
    :param tol: 最小差值（没有使用）
    :param limit: 位置限制
    :param vlimit:速度限制
    :param w:惯性权重
    :param c1:自我学习因子
    :param c2:总体学习因子
    :param f:适应度函数
    :return:最小值点
    '''

    #生成N行d列的随机点
    points=np.random.uniform(limit[0],limit[1],[init,demensions])
    #初始各个随机点的速度
    v=np.random.rand(init,demensions)
    #每个个体的最佳位置
    indiviual_best=copy.deepcopy(points)
    #整个种群的历史最佳位置
    tot_best=np.zeros(demensions)
    #每个个体的历史最佳适应度
    f_indiviual_best=np.array([float('inf') for i in range(init)])
    #种群的历史最佳适应度
    f_tot_best=float('inf')
    record=[]
    plt.figure(1)
    scale=np.arange(limit[0],limit[1],0.1)
    plt.plot(scale, f(scale))
    plt.scatter(points,f(points),c='g')
    plt.title('initial state')
    plt.ion()
    plt.figure(2)
    scale=np.arange(limit[0],limit[1],0.1)
    plt.plot(scale, f(scale))
    plt.scatter(points,f(points),c='r')
    #迭代更新
    for i in range(iters):
        fx=f(points) #个体的适应度
        #更新个体历史适应度
        for i in range(init):
            if fx[i]<f_indiviual_best[i]:
                f_indiviual_best[i]=fx[i]
                indiviual_best[i]=points[i]
            #更新种群历史适应度最小值
            if min(f_indiviual_best)<f_tot_best:
                f_tot_best=min(f_indiviual_best)
                index=np.argmin(f_indiviual_best)
                tot_best=indiviual_best[index]
        #更新速度
        v=v*w+c1*np.random.rand(1)*(indiviual_best-points)+np.random.rand(1)*c2*(tot_best-points)
        #边界速度处理，超速的和太慢的都要修改
        v[v>vlimit[1]]=vlimit[1]
        v[v<vlimit[0]]=vlimit[0]
        #位置更新
        points=points+v
        #边界位置处理
        points[points>limit[1]]=limit[1]
        points[points<limit[0]]=limit[0]
        #记录当前的适应度最小值
        record.append(f_tot_best)
        plt.clf()
        plt.plot(scale, f(scale))
        plt.scatter(points, f(points),c='r')
        plt.pause(0.1)
    plt.ioff()
    plt.show()
    #print(record)
    return tot_best

#模拟退火版的粒子群算法
def PSO_SA(init,demensions,iters,tol,limit,vlimit,w,c1,c2,f):
    '''
    粒子群搜索求解(求最小值)
    :param init:初始化多少只鸟
    :param demensions: 数据维度
    :param iters: 最大迭代轮数
    :param tol: 最小差值（没有使用）
    :param limit: 位置限制
    :param vlimit:速度限制
    :param w:惯性权重
    :param c1:自我学习因子
    :param c2:总体学习因子
    :param f:适应度函数
    :return:最小值点
    '''
    # 模拟退火的初始值
    T0 = 100  # 初始温度
    T = T0  # 迭代中温度会发生改变，第一次迭代时温度就是T0
    Lk = 100 # 每个温度下的迭代次数
    alfa = 0.95 # 温度衰减系数
    beta=0.9 #c1衰减系数(自学习)
    theta=0.95 #c2衰减系数(总体学习)
    gamma=0.9 #惯性权重衰减系数
    #生成N行d列的随机点
    points=np.random.uniform(limit[0],limit[1],[init,demensions])
    #初始各个随机点的速度
    v=np.random.rand(init,demensions)
    #每个个体的最佳位置
    indiviual_best=copy.deepcopy(points)
    #整个种群的历史最佳位置
    tot_best=np.zeros(demensions)
    #每个个体的历史最佳适应度
    f_indiviual_best=np.array([float('inf') for i in range(init)])
    #种群的历史最佳适应度
    f_tot_best=float('inf')
    record=[]
    plt.figure(1)
    scale=np.arange(limit[0],limit[1],0.1)
    plt.plot(scale, f(scale))
    plt.scatter(points,f(points),c='g')
    plt.title('initial state')
    plt.ion()
    plt.figure(2)
    scale=np.arange(limit[0],limit[1],0.1)
    plt.plot(scale, f(scale))
    plt.scatter(points,f(points),c='r')
    # 模拟退火过程
    for iteration in range(iters):  # 迭代maxgen次
        for i in range(Lk):  # 每个温度下的迭代次数
            new_points=points+v #新解
            #边界位置处理
            new_points[new_points>limit[1]]=limit[1]
            new_points[new_points<limit[0]]=limit[0]
            f_new=f(new_points)
            f_old=f(points) #个体的适应度
            #更新个体历史适应度
            for i in range(init):
                if f_new[i]<f_indiviual_best[i]: #小于个体最小适应度，直接更新
                    f_indiviual_best[i]=f_new[i]
                    indiviual_best[i]=new_points[i]
                #以一定概率接受更差的解
                else:
                    # 以一定概率接受更差的解
                    p = np.exp(-(f_new[i] - f_indiviual_best[i]) / T)
                    r = np.random.uniform(0, 1)
                    #接受
                    if r < p:
                        new_points[i]=new_points[i]
                    #不接受
                    else:
                        new_points[i]=points[i] #用之前的位置，不进行更新
                #更新种群历史适应度最小值
                if min(f_indiviual_best)<f_tot_best:
                    f_tot_best=min(f_indiviual_best)
                    index=np.argmin(f_indiviual_best)
                    tot_best=indiviual_best[index]
            points=new_points
            #更新速度
            v=v*w+c1*(indiviual_best-points)+c2*(tot_best-points)
            #边界速度处理，超速的和太慢的都要修改
            v[v>vlimit[1]]=vlimit[1]
            v[v<vlimit[0]]=vlimit[0]
        #记录当前的适应度最小值
        record.append(f_tot_best)
        plt.clf()
        plt.plot(scale, f(scale))
        plt.scatter(points, f(points),c='r')
        plt.pause(0.1)
        T = alfa * T
        c1*=beta
        c2*=theta
        w*=gamma
    plt.ioff()
    plt.figure(3)
    plt.plot(np.arange(1,iters+1),record)
    plt.show()
    return tot_best
if __name__=='__main__':
    scale=np.arange(0,50,0.1)
    # plt.figure(1)
    # plt.plot(scale,f(scale))
    # plt.show()
    #print(PSO_org(20,1,50,0.1,[0,50],[-10,10],0.8,0.5,0.5,f))
    print(PSO_SA(20, 1, 50, 0.1, [-50, 50], [-10, 10], 2, 1, 1, f))