【阅读论文】时间序列数据清洗:一项调查
文章目录
-
- 摘要
- 一、引言
-
- A.问题陈述
- B.问题挑战
- C. 组织
- 二、基于平滑的清洗算法
-
- A.移动平均
- B.自动注册
- C.卡尔曼滤波模型
- D.总结和讨论
- 三、基于约束的混合算法
-
- A. 顺序依赖 (OD)
- B.序列相关性
- C.速度约束
- D.总结和讨论
- 四、基于统计的CLEANING算法
-
- A.最大似然
- B.马尔可夫模型
- C.二项抽样
- D.时空概率模型
- E.其他人
- 五、时间序列异常检测
-
- A.异常点检测
- B.异常序列检测
- C.具有噪声的应用程序的基于密度的空间集群
- D.生成性对抗网络
- E、长时间短时记忆
- F.总结和讨论
- 六、工具和评价标准
-
- A.工具
- B.评价标准
- 七、结论和未来方向
摘要
误差在时间序列数据中普遍存在,在工业领域尤为普遍。错误的数据无法存储在数据库中,导致数据资产丢失。目前,为了处理这些包含错误的时间序列,除了保留原始错误数据、丢弃错误数据和手动检查错误数据外,我们还可以使用数据库中广泛使用的清洗算法对时间序列数据进行自动清洗。本调查提供了时间序列数据清洗技术的分类,并全面回顾了每种类型的最先进的方法。此外,我们还总结了来自研究和行业的数据清理工具、系统和评估标准。最后,我们强调了时间序列数据清洗的可能方向。
关键词:数据清洗,数据质量,时间序列。
一、引言
时间序列数据可以定义[128]为随机变量序列,x1,x2,xn,其中随机变量lex1表示序列在第一个时间点所取的值,变量x2表示第二个时间段的值,xn表示第n个时间周期的值,依此类推。时间序列已被广泛应用于许多领域[11]、[16]、[49],如金融经济、气象学和水文学、信号处理、工业制造等。时间序列数据在工业中很重要,因为工业环境中有各种传感器设备不间断地捕捉数据。由于传感器设备的数据往往不可靠[53],时间序列数据往往很大且脏。在金融领域,时间序列数据最重要的应用是预测未来商品(股票)的价格走势。然而,金融领域的时间序列错误也非常普遍,甚至一些被认为相当准确的数据集仍然存在错误的数据。例如,雅虎财经的股票信息正确率为93%。时间序列中的错误、冲突和不一致的成本和风险引起了企业和政府机构的广泛关注。在最近的工作中,研究了时间序列数据中的数据质量问题,因为由于时间序列数据存在自相关、趋势、季节性和差距,这些问题对数据质量提出了独特的挑战[25]。根据Shilakes和Tylman[78]的数据,数据质量的相关市场增长率约为17%,远高于IT行业7%的年增长率。例如,在数据仓库项目开发中,大约30%到80%的时间和成本用于数据清理。时间序列错误可以是时间戳错误或观测值错误。对于可能的时间戳错误,Song等人[80]提出了一种清理时间戳的方法。在本次调查中,我们重点关注现有的处理观测值误差的方法,因此,以下提到的时间序列误差就是观测误差。在处理时间序列数据错误时,行业中常用的处理方法有两种:
(1)丢弃错误数据。首先利用异常检测算法对时间序列进行检测,然后丢弃检测到的异常数据。
(2)清洗数据。数据清洗分为手动清洗和自动清洗。毫无疑问,人工清洗的准确率很高,但由于需要更多的时间和精力,因此难以实施。
现有的数据清理[23]、[50]的调查主要总结了数据库中数据缺失、数据不一致、数据整合和错误数据的处理方法。Karkouch et al.[58]回顾了传感器数据的生成,数据质量问题形成的原因,以及提高数据质量的技术。然而,Karkouch等人[58]并没有提供现有的错误数据清理技术的详细概述。为此,本文综述了时间序列数据误差值清理的研究现状,以期为其他研究提供参考。
A.问题陈述
在本研究中,受[48]、[86]和[101]关于时间序列误差类型分类的相关研究的启发,我们将时间序列中常见的误差归纳为单点大误差、单点小误差和连续误差三类。本文以某只股票连续30个交易日的股价为例。如图1所示,详细描述了这三种错误类型的特征。图中红线表示该股票连续30个交易日的真实价格,蓝线表示某网站抓取的股票价格。由于各种原因,观测值可能与实际值不一致。可以看到,在8-11连续4个交易日中,观测值均为0,真实值分别为1.3、1.2、1.1、1.15,第20个交易日观测值为2.4,真实值为1.3,第25个交易日观测值为1,真实值为1.3。

(1)连续误差。所谓连续误差,就是在时间序列中,误差发生在连续的几个时间点上。具体来说,连续误差可以继续细分为几种类型[86],但这里不再详细说明。图1中从第8个交易日到第11个交易日的观测值均为0,即这里出现连续误差。连续错误在现实生活中很常见。例如,当有人拿着智能手机走在路上时,附近的高楼可能会对收集到的GPS信息产生持久的影响。此外,系统误差也会引起连续误差。
(2) 一个大错误。单点误差是指在时间序列中不连续发生的误差,并且仅在间隔的单个数据点上发生。大误差意味着数据点的观测值与真实值相去甚远。值得注意的是,误差的大小与数据集的真实情况是相对的,并且密切相关。如图1中第20个交易日所示,观测值与真实值相差1.1。与第25个交易日观测值与真实值相差0.3相比,该数据点的误差较大,因此该数据点误差为单个较大误差。单点大误差在日常生活中也很常见。例如,当在路上颠簸时,光标记录的机动车油位数据可能会导致一个大错误。
(3)一个小错误。类似于单点大误差,即误差不会连续发生,只在间隔的单个数据点上发生。当数据点的观测值与真实值相差很小的距离时,即图1中的第25个交易日,为单点小误差。正如b[10]中所述,单点小错误背后的基本原理是人们或系统总是试图最小化可能的错误。例如,人们在复制文件时可能只会有一些小的遗漏。
(4)翻译错误。如图2所示,其中x轴表示时间,y轴表示对应时间的值,红线表示真值,蓝线表示平移后的误差值,这类误差的解决方法并没有上面提到的那么多。

忽略时间序列错误通常会导致查询分析等一系列应用程序无法预测的结果。因此,时间序列清洗算法对于挖掘数据的潜在价值非常重要。本文综述了时间序列数据的清洗算法和异常检测算法。通过对现有方法的总结,为对时间序列数据清洗感兴趣的学者提供参考或指导,并在此基础上讨论了时间序列数据清洗课题可能面临的挑战和未来的工作。
B.问题挑战
对于时间序列数据清洗的问题,通过调查发现了以下四个难点:
(1) 数据量大,错误率高。时间序列数据的主要来源是传感器采集。特别是在工业领域,分布在整个机器上的传感器不断实时监控机器的运行。这些传感器通常以秒的频率收集数据,并且收集的数据量相当大。例如,风电公司设备的传感器采集间隔为7秒,每台机器有2000多个工作状态数据,每天采集3000多万条数据,因此一天的工作状态数据可能超过600亿。然而,传感器收集的数据往往不够准确,有些数据由于观测的物理量而难以准确测量。例如,在炼钢厂中,由于受到环境干扰的影响,连铸坯的表面温度无法准确测量,或者可能由于传感器本身的功率而导致变形。
(2)产生时间序列数据误差的原因比较复杂。人们总是试图避免时间序列错误数据的产生,然而,时间序列错误是多种多样的。除了我们上面提到的各种原因导致的观测误差外,Karkouch等人也详细解释了各种复杂环境下产生的物联网数据误差。物联网数据是一种常见的时间序列数据,它的广泛存在确实是在世界范围内。时间序列误差产生的复杂原因也是我们在数据清理和分析中所面临的不同于传统关系数据的挑战。
(3)连续生成和存储时间序列数据。时间序列数据与关系数据最大的区别在于时间序列是连续的。因此,对于时间序列数据,清洗算法支持在线操作(实时操作)是很重要的。在线异常检测或清洗算法可以实时监控物理量,发现问题后及时报警或进行合理清洗。因此,时间序列清洗算法不仅要支持在线计算或流计算,而且要有良好的吞吐量。
(4)最小修改原则[1],[22],[35]。时间序列数据通常包含许多误差。大多数广泛使用的时间序列清洗方法都利用平滑滤波的原理。这种方法可能会对原始数据造成太大的改变,导致原始数据中包含的信息丢失。数据清理需要避免改变原有的正确数据。应以最小修改原则为基础,即变化越小越好。
C. 组织
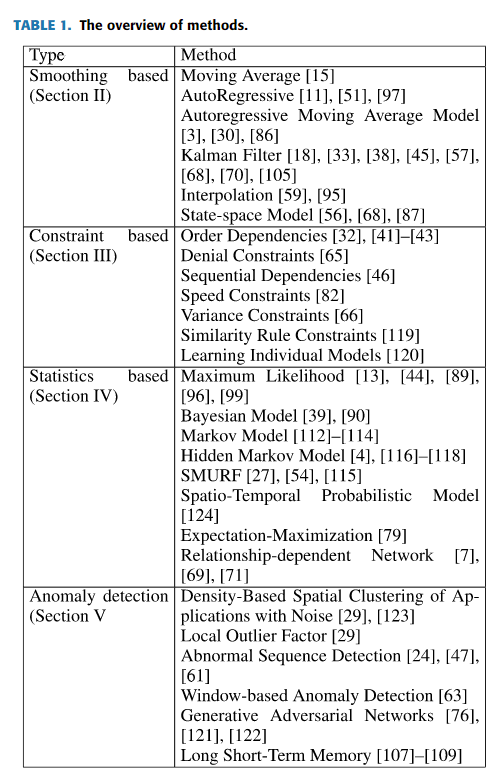
不同的算法以不同的方式解决这些挑战,通常包括基于平滑的方法、基于约束的方法和基于统计的方法,如表1所示。此外,一些时间序列异常检测算法也可以有效地清洗数据。本文的其余部分组织如下。上述四种算法分别从第二节到第五节讨论。在第六节中,我们将介绍现有的时间序列清洁工具、系统和评估标准。最后,我们在第七部分对本文进行了总结,并讨论了可能的未来发展方向。
二、基于平滑的清洗算法
平滑技术通常用于消除数据噪声,尤其是数字数据噪声。低通滤波是一种简单的算法,它滤除了数据集的较低频率。这类技术的特点是时间开销小,但由于原始数据可能会被修改很多,这会使数据失真,并导致分析结果的不确定性,因此在时间序列清理中使用的应用并不多。平滑技术的研究主要集中在移动平均(MA)[15]、自回归(AR)[11]、[51]、[97]和卡尔曼滤波模型[57]、[68]、[70]等算法上。因此,本章主要介绍这三种技术及其扩展。
A.移动平均
移动平均(MA)序列算法[15]广泛应用于时间序列平滑和时间序列预测。简单移动平均(SMA)算法:计算最近观测到的N个时间序列值的平均值,用于预测t时刻的值。简单定义如式(1)所示。
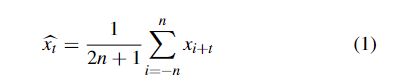
在式(1)中,* xt是xt的预测值,xt表示时刻t的真实值,2 * n + 1是窗口大小(计数)。对于时间序列x(t) = 9.8, 8.5, 5.4, 5.6, 5.9, 9.2, 7.4,为了简单起见,我们使用n = 3, k = 4的SMA,然后根据式(2)计算。
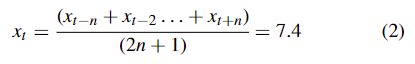
为了消除错误或噪声,数据 x(t) 可以被认为是滑动窗口的某个时间窗口,然后在给定区间 2n + 1 上连续计算局部平均值以过滤掉噪声(错误数据)并获得更平滑的测量。
在加权移动平均 (WMA) 算法中,窗口中不同相对位置的数据点具有不同的权重。通常定义为:
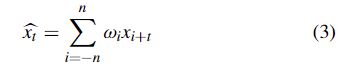
在等式(3)中,ωi表示i位置数据点对t位置数据点的影响权重,其他定义遵循上面的例子。一个简单的策略是离两个数据点越远,相互影响越小。例如,一个自然的想法是两个数据点之间的距离的倒数作为它们相互影响的权重。类似地,指数加权移动平均 (EWMA) 算法 [38] 中每个数据点的权重随着距离的增加而呈指数下降,这主要用于不稳定时间序列 [17], [52]。
为了满足传感器数据清洗的快速响应,Zhuang 等人。 [105] 提出了一种智能加权移动平均算法,该算法通过从传感器收集的置信度数据计算加权移动平均线。张等人。 (13) 提出了一种基于多阈值控制和近似正变换的方法来清理探测车辆数据,并使用加权平均方法和指数平滑方法填充丢失的数据。Qu 等人。 [18] 首先使用基于集群的异常检测方法,然后使用指数加权平均进行数据修复,用于在分布式环境中清理功率数据。
B.自动注册
自回归 (AR) 模型是一个过程,它使用自身作为回归变量,并使用前 k 个随机变量的线性组合来描述时间 t 随机变量的线性回归模型。AR模型[51]、[88]的定义,如式(4)所示。
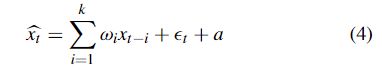
在等式 (4) 中,̂ xt 是 xt 的预测值,xt 表示时间 t 的真实值,k 是阶数,μ 是过程的平均值,푡t 是白噪声,ωi 是模型的参数,a 是常数。
Park等人[72]使用标记数据y提出了一种基于AR模型的外生输入(ARX)模型的自回归:
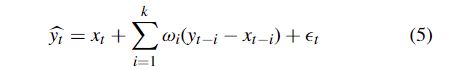
在等式 (5) 中,̂ yt 是 xt 的可能修复,而其他的则与上述 AR 模型相同。Alengrin 和 Davier [3] 提出了自回归移动平均 (ARMA) 模型,该模型由 AR 模型和 MA 模型组成。除此之外,高斯自回归移动平均模型定义为等式 (6) ϵ 所示。
![]()
在等式(6)中,8(B) = 1 - 811B -。− 8pBp 和 θ (B) = 1 − θ1B −。− θqBq 分别是度数 p 和 q 的 B 中的多项式,θ0 是常数,B 是反向移位算子,使得 BZt = Zt−1,xt 是均值 μ = 0 和方差 σ 2x 的独立高斯变量序列。Box 和 Pierce [12] 提出了一种基于 ARMA 模型的更复杂的自回归综合移动平均 (ARIMA) 模型,这里没有详细描述。Akouemo 和 Povinelli [2] 提出了一种将 ARX 和人工神经网络 (ANN) 模型相结合的清洁时间序列方法,该模型执行假设检验以检测残差的极值,并使用 ARX 和 ANN 模型修复异常数据点。Dilling 和 MacVicar [30] 使用 ARMA 模型清理高频速度剖面数据,Chen 等人。 [21] 使用 ARIMA 模型清理风电数据。
C.卡尔曼滤波模型
卡尔曼57提出了卡尔曼滤波理论,可以处理时变系统、非平稳信号和多维信号。卡尔曼滤波器创造性地将错误(预测和测量错误)合并到计算中,错误独立存在,不受测量数据的影响。卡尔曼模型涉及概率、随机变量、高斯分布和状态空间模型等。考虑卡尔曼模型涉及太多的内容,这里没有给出特定的描述,只给出一个简单的定义。首先,我们引入了一个离散控制过程系统,该系统可以通过线性随机差分方程来描述,如等式 (7) 所示。
![]()
此外,系统的测量值表示为等式(8)所示。
![]()
在方程(7)和(8)中,xt是时间t处的系统状态值,vt是时间t时系统的控制变量值。m和n是系统参数,对于多模型系统,它们是矩阵,yt是时间t的测量值,r是测量系统的参数,并且对于多测量系统,r是矩阵,p(k)和q(k)分别表示过程和测量的噪声,假设它们是高斯白噪声。
扩展卡尔曼滤波器是递归非线性系统应用最广泛的估计,因为它只是简单地线性化非线性系统模型。然而,扩展卡尔曼滤波器有两个缺点:线性化可以产生不稳定的滤波器,很难实现雅可比矩阵的推导。因此,Ma 和 Teng [67] 提出了一种基于无气味卡尔曼滤波器预测 Mackey-Glass 方程的新方法来解决这些问题。在信号处理领域,有很多基于卡尔曼滤波的工作[18],[33],[45],但这些技术还没有广泛应用于时间序列清洗领域。Gardner [38] 提出了一种基于核卡尔曼滤波器的新模型来执行各种非线性时间序列处理。庄等人。 [105] 使用卡尔曼滤波器模型来预测传感器数据并使用 WMA 对其进行平滑处理。
D.总结和讨论
如表 2 所示,有许多基于平滑的方法,例如状态空间模型 [6, 8], 27] 和插值 59, 0.95。状态空间模型假设系统随时间的变化可以由不可观察的词序列决定,时间序列与可观察序列之间的关系可以由状态空间模型确定。通过建立状态方程和观察方程,状态空间模型提供了一个模型框架来充分描述动态系统的时间特征。为了使这种平滑算法具有更好的效果,许多研究 [20], 2017] 还提出了各种技术来估计上述方法中的参数。大多数平滑技术,清理时间序列时,开销很小,但更改原始正确数据点非常容易,这极大地影响了清理的准确性。换句话说,改变了正确的数据,这会扭曲分析结果并导致结果的不确定性。

三、基于约束的混合算法
在本节中,我们介绍了几种典型的算法,包括顺序依赖 (OD) [32]、顺序依赖 (SD) [46] 和速度约束 (24),用于修复时间序列错误。
A. 顺序依赖 (OD)
在关系数据库中,Order Dependencies (ODs) 是一种简单有效的方法,已被广泛研究 [32]、[41]-[43]。我们发现 OD 也适用于解决一些时间序列数据清洗问题。具体解释如下:令 x(t) = x1, x2。xt 是一个时间序列,OD 可以表示为 <, ≤, >, ≥。对于汽车 x(t) 行驶的英里数,里程应该随着时间的推移而增加。形式表示如下:t1 < t2 那么 xt1 ≤ xt2 其中 x(t) 是里程,t 是时间戳。例如,考虑表3中的示例关系实例。元组按属性序列号排序,标识从小时到小时迅速增加的海平面。

通常,等式 (9) 形式的 OD 表明 N 与 M 严格递增。例如等式(10)。
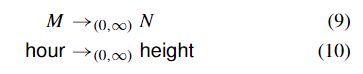
ODS和DC也可以作为数据库中错误检测和数据修复的完整性约束。Wijsen[92],[93]用时间数据库的时间维度扩展了OD。设 I = {I1, I2, I3,。} 是一个时间关系,可以看作是传统“快照”关系的时间序列,所有这些都在相同的属性集上。趋势依赖 (TD) 通过使用 {<, =, >, ≤, ≥, 6 =} 的任何算子,允许随时间比较具有线性有序域的属性。考虑约束在 I 中的 (Ii, Ii+1) 上指定。对于每个时间点 i,它需要将时间 i 的员工记录与下一个时间 i + 1 的记录进行比较,以便员工的工资永远不会减少。Lopatenko 和 Bravo [65] 提出了一种基于拒绝约束 (DC) 的数值类型数据清理方法作为约束,其原理与此类似。
B.序列相关性
Golab等人提出的顺序依赖算法。[46]侧重于时间序列中两个连续数据点之间的值差异。Golab等人[46]定义给定关系实例和嵌入 SD M →g N 的 CSD Tableau Discovery 问题,以找到最小大小的表autr,使得 CSD (M →g N , tr ) 的置信度至少为给定的阈值。CSD 可以是![]() 它指出,对于[19611.01 00:00-2016.01 00:00]中任意两个连续小时,它们的距离应始终为 > 0。一般来说,顺序依赖 (SD) 的形式为
它指出,对于[19611.01 00:00-2016.01 00:00]中任意两个连续小时,它们的距离应始终为 > 0。一般来说,顺序依赖 (SD) 的形式为
![]()
在等式(11)中,M ⊆ R 是有序属性,N ⊆ R 可以通过某些距离度量来衡量,g 是区间。它指出,当元组在 M 上排序时,任意两个连续元组的 N 值之间的距离在区间 g 内。Casado-Vara等人[19]提出了流模式的概念来表示数据流的结构和语义约束。这个概念包含各种语义信息,不仅包括数值,还包括顺序之间的属性。顺序依赖算法不仅可以用于传统的关系数据库清理,还可以用于时间序列清理。事实上,有许多基于依赖的清理算法设计用于不适合时间序列数据清理的关系数据库,例如:函数依赖 [6] (FD) 和条件函数依赖 [36]、[37] (CFD)。顺序依赖是少数基于可用于时间序列清理的依赖的算法之一。
C.速度约束
为了清理时间序列数据,Song 等人提出的基于速度约束的方法。 [82] 考虑速度对给定区间内值变化的限制。由于我们学习了一些常识,例如鸟的最大飞行速度、一天中的温度、汽车里程等。考虑时间窗口 T 是时间序列 x = x1, x2, 上的一对最小速度 Smin 和最大速度 Smax。, xt ,其中每个 xi 是第 i 个数据点的值,时间戳 i。
例如,考虑时间序列:
![]()
其中时间戳 t = {1, 2, 3, 4, 5, 6, 7, 8, 9}。值属性对应于 x,而表 4 中的时间属性表示时间戳。


通常,速度约束以等式(12)的形式。
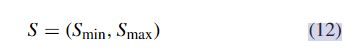
如果时间序列数据x满足速度约束S,则对于时间窗口T中的任何xi, xj,其Smin < xj−xij−i < Smax。在实际应用中,速度约束通常对特定时间段有效。例如,在考虑汽车最快的速度时,参考的时间段通常几个小时,没有考虑不同年份的两个数据点。速度约束 S 的值可能是正的(约束值增长率)或负的(约束值的下降率)。在处理小误差时,速度约束效果较差,Yin等人[66]对方差约束进行了进一步的研究,利用方差阈值V来衡量给定W窗口中时间序列的离散程度。
D.总结和讨论
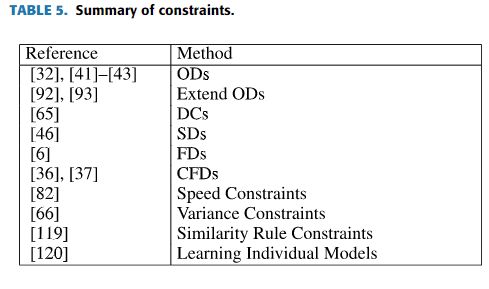
在关系数据库领域,有许多基于完整性约束的清理算法,这些算法很难应用于观测值基本上是数字的时间序列领域,因为它们遵循严格的等式关系。我们在表(5)中总结了一些方法,这些方法可以用于时间序列数据清理,例如OD和SD可以用于解决某些情况下的问题,例如汽车的里程数不减少。进一步的基于速度的约束可以用于处理GPS和股价等数据,但只有具有相关的领域知识才能给出合理的约束。因此,基于约束的清洗算法需要进一步改进才能具有更好的鲁棒性。Song等人[119]提出的相似性规则约束和Zhang等人[120]提出的学习个体模型适用于修复缺失的数据。一个可能的未来方向是使用异常检测方法首先检测异常,然后将异常值视为缺失进行修复。我们将在第五节中讨论异常检测。
四、基于统计的CLEANING算法
基于统计的清理算法在数据清理领域占有重要地位。这些算法使用从数据中学习到清理数据的模型。基于统计的方法涉及很多统计知识,但本文侧重于基于统计的数据清理方法,因此我们不会详细介绍与统计相关的知识。
A.最大似然
最大似然原理的直观概念是随机检验,如果有几种可能的结果x1, x2…Xt,如果在一次试验中出现结果xi,则一般认为试验条件对xi有利,或认为xi的出现概率最高。
符号:对于给定时间序列数据x(t),其符合概率分布d,假设其概率聚合函数(离散分布)为Fd;考虑一个分布参数θ,采样x1, x2…xn,则用Fd计算其概率[13],如式(13)所示。
![]()
Gogacz和S. toruzynk[44]使用最大似然技术清理射频识别(RFID)数据。Wang等人[89]提出了第一个极大似然解决方案,以解决从嘈杂的社会感知数据中发现真相的挑战。Yakout等人[96]提出了一种新的数据修复方法,该方法基于最大化给定数据分布中替换数据的可能性,可以使用统计机器学习技术对其建模,但该技术用于修复数据库的数据。
对于时间序列数据误差的修复,Zhang等[99]提出了基于最大似然的更好的解决方案,从概率的角度解决了问题。根据时间序列中相邻数据点速度变化的概率分布,可以将时间序列清洗问题转换为一个被清洗的时间序列,该时间序列是基于具有最大可能性的速度变化概率。
B.马尔可夫模型
马尔可夫过程是一类随机过程,即过程中每个状态的转变只依赖于前n个状态。这个过程被称为n -序模型,其中n是影响过渡状态的数字。最简单的马尔可夫过程是一阶过程,每个状态的转变只依赖于它之前的状态。时间和状态是离散马尔可夫过程,称为马尔可夫链,缩写为Xn = X (n), n = 0,1,2 … …马尔可夫链[112]是一个随机变量序列x1, X2, X3 … …这些变量的值域,即它们所有可能值的集合,称为“状态空间”,Xn的值就是时间n的状态。
马尔可夫模型[113],[114]是一种基于马尔可夫链的统计模型,广泛应用于语音识别、词性自动标注、语音转换、概率语法等自然语言处理应用中。为了找到随时间变化的模式,马尔可夫模型试图构建一个可以生成模式的流程模型。文献[114]和[113]使用了特定的时间步长、状态,并进行了马尔可夫假设。有了这些假设,这种生成模式系统的能力就是马尔可夫过程。马尔可夫过程由初始向量和状态转移矩阵组成。关于这个假设需要注意的一点是,状态转移概率不随时间变化。
隐马尔可夫模型(HMM)[116],[117]是一种基于马尔可夫模型的统计模型,用于描述具有隐式未知参数的马尔可夫过程。难点在于从可观测参数中确定过程的隐式参数,然后利用这些参数进行进一步的分析,比如对时间序列数据的预测。例如,在掷骰子10次后,我们可以得到一串数字,例如,我们可能会得到这样一串数字:1、4、5、3、3、1、6、2、4、5,如图4所示。这串数字被称为可见状态链。但是在HMM中,我们不仅有这样一串可见的状态链,还有一串隐含的状态链。在这个例子中,隐式状态链可能是:D5, D3, D2, D3, D4, D6, D1, D5, D1, D2。
Gupta和Dhingra[118]使用HMM来预测股票价格。Baba et al.[4]提出了一种基于HMM的数据清洗方法,用于清洗与地理位置信息相关的RFID数据。在多维时间序列清洗中,HMM由于维度之间的相关性,具有比一维清洗算法更大的应用空间。

C.二项抽样
Jeffery等人[54]提出了一种用于清洗RFID数据的自适应方法,该方法利用基于采样和平滑理论的技术来提高RFID数据的质量。标签转移检测:标签转移检测是指当标签的位置发生变化时,清洗结果应反映标签离开的事实。让我们介绍一些与rfid相关的概念。
(1)讯问循环:阅读器对标签的问答过程是阅读器检测标签的基本单元。
(2)阅读器读取周期(epoch, 0.2秒- 0.25秒):多个查询周期的集合。
基于上述概念,定义如下:Wii是标签i的平滑窗口,由ωi个纪元组成,Si是Wi窗口中实际检测到标签i的窗口,Countt表示t个纪元的查询周期数,R是对应的t个纪元标签i的个数。对于给定的时间窗口,假设每个纪元内标签i被读取的概率为pi=R / Countt,不可靠RFID数据的统计平滑(SMurf)[54]算法将每个纪元对标签的读取视为概率pi的伯努利实验。因此,pi服从二项分布B(ωi,pi)。Pi,avg是以Si为单位的平均读取速率。
使用基于伯努利实验的模型来观察标签i,如果标签的平均读取率为(1−pi,ω)ωi。为了确保标签的动态性质,需要满足滑动窗口Wi的大小,如公式(14)所示。
![]()
SMURF算法首先将初始窗口大小设置为1,然后根据读取的实际情况动态调整窗口长度。如果当前窗口满足完整性要求[54],SMURF算法将检测标签的状态。当检测结果表明标签状态发生变化时,SMURF会将当前窗口长度调整为原始窗口的1/2,以对标签的转换做出反应。如果计算出的满足完整性约束的窗口大小大于当前窗口大小,则算法将当前窗口大小线性增加2步,并输出当前窗口中的点数据。如果检测到标签没有移动,则算法输出当前窗口中点作为输出点,然后继续滑动历元以进行下一次处理。
SMurf算法被广泛应用于清理RFID数据,许多研究[27]、[115]对其进行了改进。Leema等人。[27]研究了标签移动速度对数据去除效果的影响。[115]考虑数据冗余对设置滑动窗口的影响。
D.时空概率模型
除了数据清理,Milani等人。[124]提出时空概率模型(STPM),该方法从历史数据中学习更详细的数据模式,然后对当前数据进行清洗。STPM不仅给出了在不同时间对数据集进行更新的联合概率分布,而且还区分了关联更新和关联值。STPM是基于动态概率关系模型(DRPM)的,因此首先需要对DRPM模型进行描述。DRPMS是一种用于表示动态数据集之间关系的图模型,其模型基于属性之间的依赖关系,一般使用条件概率分布来计算每个属性值在给定父节点值中的概率并形成关系链。例如,当我们需要估计时间T的数据时,我们只能使用时间T之前的数据来推断,即当前状态仅取决于先前的状态,这类似于马尔可夫模型。STPM扩展了DRPM来模拟不同时间数据之间的更新模式,并通过对更新事件的建模来捕获空间和时间的更新模式,以提供可能存在的更新关系,最终检测和修复数据。
E.其他人
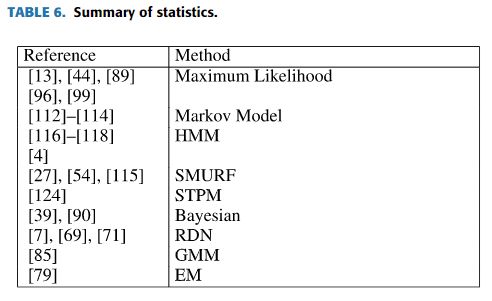
首先,我们在表(6)中总结了上述方法。事实上,贝叶斯预测模型是一种基于贝叶斯统计的技术。贝叶斯预测模型利用了模型信息、数据信息和先验信息,因此预测效果良好,因此该模型被广泛应用,包括在时间序列数据清理领域。Wang等人[90]建立了贝叶斯分析的成本模型,用于分析数据中的错误。Bergman等人[7]考虑用户的参与,并使用用户对查询结果的反馈来清理数据。Mayfield等人[69]提出了一种更复杂的关系相关网络(RDN[71])模型来对属性之间的概率关系进行建模。RDN与传统关系依赖(如贝叶斯网络[39])的区别在于,RDN可以包含环结构。该方法迭代清理数据集,并观察每次清洗前后数据集概率分布的变化。当数据集的概率分布收敛时,清理过程中止。Zhou和Tung[104]提出了一种通过使用GPU加速高斯模型学习的技术。文章认为,在数据过多的情况下,没有必要使用所有的数据来学习模型。此外,作者还提供了一种自动调整的方法。为了清理和修复燃油液位数据,Tian等人[85]提出了一种基于同步迭代方法的改进高斯混合模型(GMM),该模型使用粒子群优化算法和最速下降算法来优化GMM的参数,并使用基于线性插值的算法来校正数据误差。Shumway和Stoffer[79]使用EM[28]算法与空间状态模型[56]、[70]相结合来预测和平滑时间序列。
五、时间序列异常检测
Gupta等人[48]研究时间序列数据的异常检测方法:对于给定的时间序列数据,可能存在两种类型的异常,即单点异常和后续异常(连续异常)。在这一部分中,我们首先讨论了异常点和异常序列的检测方法,然后介绍了基于密度的带噪声应用的空间聚类(DBSCAN)算法在数据清洗中的应用,然后回顾了与机器学习相关的异常检测方法。
A.异常点检测
对于单点异常,最常见的想法是使用预测模型进行检测。也就是说,将建立的模型的预测值和每个数据点的观测值进行比较,如果这两个值之间的差值大于某个阈值,则观测值被认为是异常值。具体而言,Basu和Meckesheimer[5] 以时间戳t为中心点,选择所有时间戳为pst−k到t+k的数据点,这些数据点的中值被认为是时间戳为t值的数据点的预测值。Hill和Minsker[51]首先对数据点进行聚类,并将聚类的平均值作为该点的预测值。AR模型和ARX模型被广泛用于经济学、社会调查[11]、[16]等各个领域的异常检测。ARX模型利用了人工标记的信息,因此在清理数据时比AR模型更准确。ARIMA模型[102]代表了一种由上述AR和MA组成的时间序列模型,可用于非平稳时间序列的数据清理。Kontaki等人[63]提出对数据流中基于距离的异常值进行连续监测。最广泛使用的定义之一是基于距离的定义,如图5所示:如果给定距离内的对象少于k个,则将对象p标记为异常值。这里k=4,q是正常点,p是异常点。

B.异常序列检测
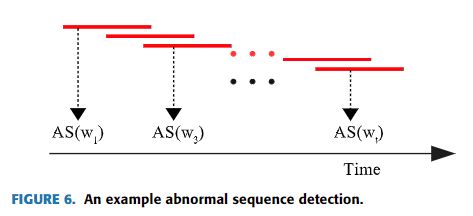
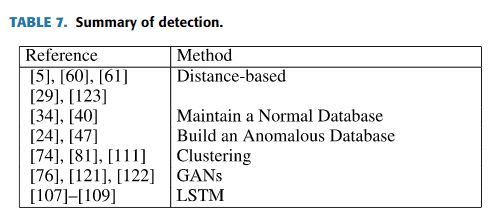
不同的研究对子序列异常有不同的定义。Keogh等人[61]提出了子序列异常,即子序列与最近的非重叠匹配的距离最大。有了这个定义,最简单的计算方法是计算每个长度为n的子序列与其他子序列之间的距离。当然,这种计算方法的时间复杂度非常高。在后来的研究中,Keogh等人[60]提出了一种通过重新排序候选子序列的启发式算法,Wei等人[91]提出了一个使用局部敏感哈希值的加速算法。在计算距离时,通常使用欧几里得距离,Keogh等人[62]进一步提出了一种使用基于压缩的相似性度量作为距离函数的方法。如图6所示,数据被划分为多个子序列,这些子序列相互重叠。首先计算每个窗口的异常分数,然后根据每个窗口的非正常分数(AS)计算整个测试序列的非正常得分(AS)。与作为异常值的整个时间序列的直接输出相比,基于窗口的技术可以更好地定位异常。基于这种技术的方法主要有两种。一种是维护一个正常的数据库[34],[40],然后将测试序列与正常数据库中的序列进行比较,以确定是否异常;另一种是建立一个异常数据库[24],[47],然后将测试序列与数据库中的序列进行比较,以检测其是否异常。
C.具有噪声的应用程序的基于密度的空间集群
DBSCAN[111]算法是一种基于密度可达关系的聚类方法,它将密度足够大的区域划分成簇,在空间数据库中找到带有噪声的任意形状的簇,并将簇定义为按密度连接的最大点集。然后,该算法根据设定的密度阈值定义簇作为划分簇的依据,即当满足该阈值时,就可以认为它是一个簇。
DBSCAN算法的原理是:(1)DBSCAN通过检查数据集中每个点的EPS邻域来搜索聚类。如果Pointp的EPS邻域包含的点比MinPts多,则创建一个以p为核心对象的集群;(2)然后,DBSCAN迭代地聚合可从这些核心对象直接到达的对象。该过程可能涉及对一些密度可达的簇进行合并;(3)当没有新的点被添加到任何簇时,该过程结束。
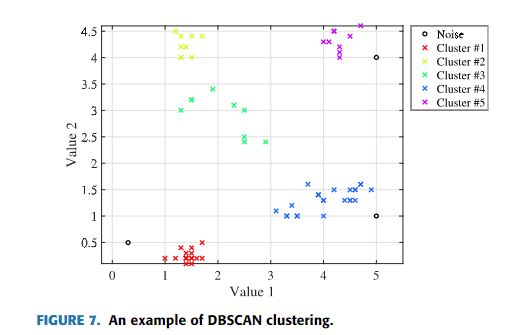
其中MinPts是给定点成为邻域中核心对象的最小邻接点数量,EPS是邻域半径。例如,Epsis 0.5和MinPts为3,对于给定的数据集,聚类的效果如图7所示。一些噪声点可以修复并聚类到它们相邻的类中。最近的研究[81]表明,在修复错误数据之后。并对基于DBSCAN的GPS数据进行了清洗实验,提高了空间数据的聚类精度。但该方法不能解决连续误差问题,需要进一步改进。
D.生成性对抗网络
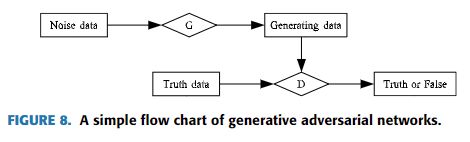
随着机器学习技术的快速发展,越来越多的问题通过机器学习得到解决。Li等人[76]使用GANs网络来有效地检测时间序列数据中的异常。GANs同时训练两个模型,这两个模型是用于捕捉数据分布的生成模型和用于区分数据是真实数据还是伪数据的判别模型,如图8所示。
给定一个具有均匀分布概率的随机变量作为输入,我们希望生成输出的概率分布为‘’DOG概率分布‘’。生成匹配网络(GMNS)的思想是通过直接比较生成的分布和真实的分布来训练生成网络,其思想是通过重复以下步骤来优化网络:
(1)生成一些均匀分布的输入;
(2)让这些输入遍历网络并收集生成的输出;
(3)基于可用样本(例如,计算真实的狗图像样本与生成的图像样本之间的MMD距离),将真实的“狗的概率分布”与生成的“狗的概率分布”进行比较;
(4)使用反向传播和梯度下降来计算误差和更新权重。这个过程的目的是最大限度地减少生成模型和判别式的损失。
Li等人。[76]利用GANS来检测时间序列中的异常,一个自然的想法是使用GANS网络来修复时间序列数据的缺失值。也许更多的机器学习算法正在等待时间序列误差值的清理。一个简单的想法是将检测到的异常数据视为丢失的数据,然后进行修复。Sun等人。[121]首先分析车位数据与车位数据的相似性,然后利用递归遗传算法生成车位数据作为维修数据,为解决时间序列数据的维修问题提供了一种新的思路。方等人[122]提出了基于卷积神经网络(CNN)和遗传算法的FuelNet。FuelNet用于修复不一致的情况,并计算随时间推移的不完整油耗率。
E、长时间短时记忆
由于递归神经网络(RNN)也存在梯度消失的问题,给长序列数据的处理带来了困难。Gers等人。[106]改进了RNN,得到了RNN的特例长短期记忆(LSTM),避免了规则RNN梯度的消失。它在工业上得到了广泛的应用,[107]-[109]使用LSTM对时间序列数据进行异常检测。
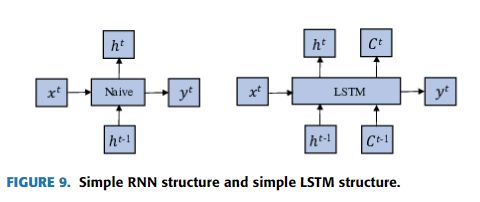
左图是简单的RNN结构图,右图是图9中的简单LSTM结构图,其中给定的函数如公式(15)所示。
![]()
在公式(15)中,xt是当前状态下的数据输入,ht−1(隐藏状态)表示接收到的前一个节点的输入,yt是当前状态下的输出,ht是传递到下一个节点的输出。从图9可以看出,输出的ht与xt和ht−的值有关1.ytis通常用于投资一个线性层(主要用于维度映射),然后使用Softmax对所需的数据进行分类。如图9所示,RNN只有一个传送状态Ht,LSTM也有一个传送状态CT(信元状态)。LSTM分为三个主要阶段:
(1)遗忘阶段。遗忘阶段主要是忘记从上一个节点传入的输入。一个简单的原则是:忘记不重要的,记住重要的。更具体地说,ZF被计算为遗忘门,其用于控制先前状态CT−1,然后决定是保留数据还是忘记数据。
(2)选择性记忆阶段。在这个阶段,输入被选择性地记忆。主要是为了记住输入的x,越重要的数据需要越保留。
(3)输出阶段。此阶段确定哪些输出将被视为当前状态。与正常的RNN类似,输出yt通常也是通过Ht变化得到的。
F.总结和讨论
除了上述方法外,我们还在表(7)中总结了一些常见的方法。如表(7)所示,Xing等人[94]表明,清理序列可以提高时间序列分类的准确性。刁等人[29]设计了基于LOF[14]的在线异常检测和清理算法。Zhang等人[100]提出了一种基于连续误差中误差时间序列时序相关性的迭代最小清洗算法,并在数据清洗中保持最小修改原则。该算法在清除时间序列数据中的连续错误方面是有效的。Qu等人[74]首先使用基于聚类的方法进行异常检测,然后使用指数加权平均进行数据修复,用于在分布式环境中清理电力数据。Corizzo等人[123]使用基于距离的方法检测异常地理数据,然后使用梯度增强树(GBT)来修复异常数据。我们可以得出结论,异常检测算法在时间序列数据清理中发挥着重要作用。为时间序列修复设计异常检测算法也变得越来越重要,我们在第七节中讨论了未来的方向。
六、工具和评价标准
在这一部分中,我们首先对时间序列清洗工具进行了概述,然后总结了与时间序列清洗方法相关的评价标准。
A.工具
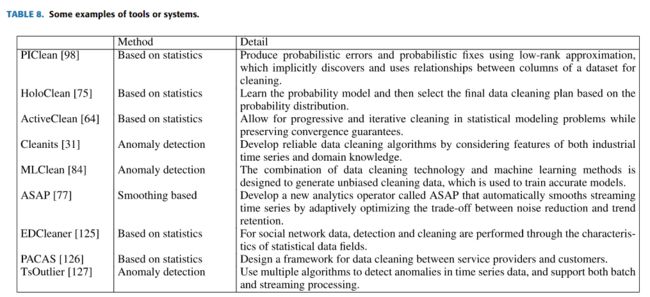
有许多用于数据清理的工具或系统,但它们在时间序列清理问题上并不有效。在表8中,我们研究了一些可能用于时间序列清理的工具,因为它们[64]、[75]、[84]、[98]最初用于解决传统的数据库清理问题。Ding等人[31]介绍了Cleanits,这是一种工业时间序列清洁系统,实现了一种用于在工业时间序列中检测和修复的集成清洁策略。Cleanits提供了一个用户友好的界面,因此用户可以在每个清洁过程中使用结果和日志可视化。此外,Cleanits的算法设计还考虑了工业时间序列和领域知识的特点。Rong和Bailis[77]提出的ASPA违反了最小修改原则,扭曲了数据,不适合广泛使用。Wang等人提出的EDCleaner。[125]是针对社交网络数据设计的,通过统计数据字段的特性进行检测和清理。Huang等人[126]提出了PACAS,它是服务提供商和客户之间的数据清理框架。Huang等人[127]提出了TsOutlier,这是一种检测异常值的新框架,并对物联网数据进行了解释。TsOutlier使用多种算法来检测时间序列数据中的异常,并支持批处理和流处理。关于时间序列清洁工具或系统的研究不多,我们将在第七节的未来方向中进一步讨论。
B.评价标准
均方根(RMS)误差[54]被用来评估清洁算法的有效性。设x表示由时间序列的真值组成的序列,x表示由添加误差后的观测值组成的序列,̂x表示由清洗后的修复值组成的序列。这里,均方根误差[54]如公式(16)所示。
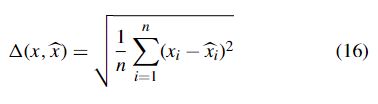 公式(16)测量真实值和净化值之间的距离。均方根误差越小,清洗效果越好。
公式(16)测量真实值和净化值之间的距离。均方根误差越小,清洗效果越好。
其他标准包括错误数据和正确数据之间的错误距离、错误数据和清理结果之间的修复距离(如公式(17)所示,参考数据修复中的最小修改原则)。

Dasu和Loh[26]提出了一种统计失真方法来评估清洁方法的质量。该方法直接观察数据集中的数值分布,并根据不同清洗方法引起的分布变化对质量进行评价。
七、结论和未来方向
本文综述了四类时间序列清洗算法、清洗工具或清洗系统以及相关的评价标准研究。接下来,我们在第七节-A节对全文进行总结,并在第七-B节列出对未来方向的一些建议。