如何从购物数据中挖掘出啤酒与尿布的关联关系？

  首先说一个关联分析的经典案例，零售业巨头沃尔玛对消费者的购物行为进行分析时发现，男性顾客在购买婴儿尿布时，通常会顺带购买几瓶啤酒来犒劳自己，于是推出了尿布和啤酒摆在一起销售的促销手段。而这个举措真的获得了巨大成功，尿布与啤酒的销量都大幅增加了。大型超市的商品超过万种，每日有过千的交易量，如何从顾客的购买行为中发现哪几种是经常在一起购买的呢，这就要用到关联分析了。
  关联分析（association snalysis）可以从大规模数据集中寻找物品间的隐含关系，上述的尿布与啤酒就是在商业领域应用中的一个经典案例。通过提取出反映顾客偏好的有用的规则，可以制定出有效的营销策略来促进销量。关联分析不仅在商业领域被广泛应用，在医疗，保险，电信和证券等领域也得到了有效的应用。在介绍实现原理之前，先讲解一下关联分析涉及的几个基本概念。

基本概念

项（item）
在购物篮事务中，一种商品就是一个项。比如，顾客购物单中的商品，啤酒和尿布都是一个项。
项集（item sets）
包含0个或多个项的集合，如果包含k个项，称为k-项集。比如，{啤酒}为1-项集，{啤酒，尿布}为2-项集。
支持度（support）
包含项集的记录在所有记录中所占的比例。我们用$\sigma$(啤酒)表示包含啤酒的记录数，用N表示所有的记录数，$s$(啤酒)表示支持度，那么{啤酒}这个项集的支持度就是：
$$s(啤酒)=\frac{\sigma (啤酒)}{N}$$
频繁项集（frequent item sets）
如果我们对项集的支持度设定一个最小阈值，那么所有支持度大于这个阈值的项集就是频繁项集。
关联规则（association rules）
其实是两个项集之间的蕴涵表达式。如果我们有两个不相交的项集P和H，就可以有规则$P\to Y$, 例如{尿布}$\to${啤酒}。项集和项集之间组合可以产生很多规则，但不是每个规则都是有用的，我们需要一些限定条件来帮助我们找到强度高的规则。
可信度（confidence）
关联规则的可信度定义为：H在包含P的记录中出现的频繁程度。还是{尿布}$\to${啤酒}这个例子，包含{尿布}的记录出现了4次，包含{尿布，啤酒}的记录也出现了3次，那么这个规则的可信度就是0.75。

发现频繁项集

  下表是一个杂货店的交易记录，包含5种商品：面包、牛奶、尿布、啤酒、可乐。

交易编号	商品
1	啤酒
2	面包，啤酒
3	尿布，啤酒
4	尿布，啤酒，可乐
5	牛奶，尿布，啤酒
6	面包，牛奶，可乐

  用A-E这5个字母代表上述5种商品，商品间的组合可以产生多少项集呢？如下图所示，包含空集在内一共32个项集。

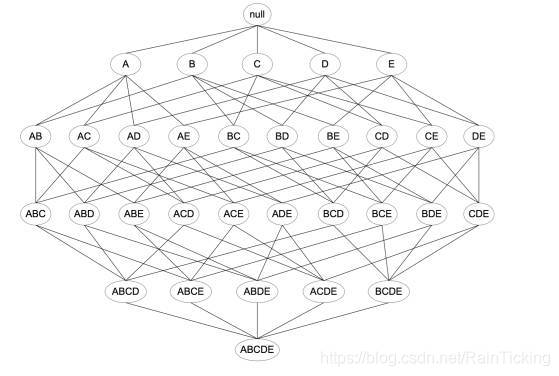
  推及到N种商品，产生的项集数为$2^N$个。即使有100种商品，也会有超过$10^{30}$种可能的项集。大型超市有万种以上的商品，机器要遍历所有的项集的代价会非常高。
  如何解决上述问题呢，这就引出了Apriori算法，它开创性的使用了基于支持度的剪枝技术来控制候选项集的指数级增长。该算法的原理是说如果某个项集是频繁的，那么它的所有子集也是频繁的。如上图给出的例子，如果{A，B}是频繁的，那么{A}与{B}也一定是频繁的。直观上看没什么帮助，但如果反过来看就有用了，如果一个项集是非频繁项集，那么它的所有超集也是非频繁的。还是上图的例子，如果{A}是非频繁项集，那么所有包含A的项集，比如{AB}、{AC}等,都是非频繁项集，也就不需要计算了。
  Apriori算法的过程是这样的，初始时，每种商品作为一个项集组成项长度为1的候选项集（1-项集）的集合；第2步，遍历候选项集（k-项集），通过计算支持度，过滤得到频繁项集（k-项集）的集合；第3步，基于上一步得到的频繁项集（k-项集），合并生成项长度+1的候选项集（k+1项集）集合；重复上述2-3 步，直到没有新的候选集可以产生。Apriori算法的伪代码为：

---

输入： 样本集 $D$ = {$x_1,x_2,...,x_n$};
       最小支持度 $minSupport$
过程：

1. 统计$D$中总记录数，记为n
2. 遍历$D$中所有记录，每种物品生成一个项集，例如$c_1$={A}，组成1-项的候选项集$C_1$={$c_1,c_2,...,c_m$}
3. repeat
4.   令k-项频繁项集：$L_k=\varnothing$
5.   令支持度计数：$SC=\varnothing$
6.   for $i=1,2,...,n$ do
7.     for $j=1,2,..|C_k|$ do
8.       if $c_j\subset x_i$ then
9.         支持度计数$S{C}_{c_j}$加1:$S{C}_{c_j}=S{C}_{c_j}+1$
10.       end if
11.     end for
12.   end for
13.   for $i=1,2,...,|SC|$ do
14.     计算项集的支持度：$s_i=\frac{S{C}_i}{n}$
15.     if $s_i>minSupport$ then
16.       将项集$S{C}_i$并入频繁项集$L_k$：$L_k\bigcup \{S{C}_i\}$
17.       将支持度$s_i$并入支持度结果集$S_k$：$S_k\bigcup \{s_i\}$
18.     end if
19.   end for
20.   for $i=1,2,...,|L_k|$ do
21.     for $j=i+1,i+2,...,|L_k|$ do
22.       对第$i$个项集$L_{ki}$与第$j$个项集$L_{kj}$排序，如果前k-1个项相同，那么将这两个项集的并集，合入到候选项集$C_{k+1}$：$C_{k+1}\bigcup \{L_{ki}\bigcup L_{kj}\}$
23.     end for
24.   end for
25. until 频繁项集$L_k$为空

输出： 频繁项集列表$L=\{L_1,L_2,...,L_k\}$
       频繁项集对应的支持度$S=\{S_1,S_2,...S_k\}$

---

挖掘关联规则

  上面介绍如何使用Apriori算法来发现频繁项集，那如何从中挖掘出关联关系呢？比如频繁项集{啤酒，尿布}，那么可能有一条关联规则“尿布$\to$啤酒”。这意味着如果有人购买了尿布，那么有很大概率会同时购买啤酒，但反过来并不一定成立。
  频繁项集的量化指标是支持度，同样地，关联规则也有量化指标可信度（confidence）。一条规则P$\to$ H，规则前件为P，规则后件为H，它的可信度计算公式为：
$$conf(P\to H)=\frac{support(P\bigcup H)}{support(P)}$$即项集P和H合并组成的项集的支持度，除以项集P的支持度。
  类似频繁项集是基于支持度剪枝生成的，关联规则也可以基于可信度的剪枝来生成。首先，一个频繁项集中的每个项作为规则后件H，生成一个H长度为1的候选规则集；第2步，计算候选规则集的可信度，过滤得到剪枝后的规则后件H；第3步，合并剪枝后的规则后件H，生成H长度+1的新的候选规则集，重复上述第2-3步，直到不能再合并为止。举例来讲，频繁项集{‘A’,‘B’,‘C’}，首先创建一个规则后件H长度为1的候选规则集[{‘A’,‘B’}$\to${‘C’}，{‘A’,‘C’}$\to${‘B’}，{‘B’,‘C’}$\to${‘A’}]，然后计算可信度，满足要求的规则集为[{‘A’,‘B’}$\to${‘C’}，{‘A’,‘C’}$\to${‘B’}]；那么就可以合并规则后件{‘C’}和{‘B’}，得到新的候选规则集[{‘A’}$\to${‘B’,‘C’}],再计算可信度，得到规则集。具体过程的伪代码如下：

---

输入： 频繁项集 $L$ = {$L_1,L_2,...,L_k$}
       频繁项集对应的支持度$S=\{S_1,S_2,...S_k\}$
       最小可信度 $minConf$
过程：

1. 初始化规则集：$R=\varnothing$
2. for $i=2,3,...,k$ do
3.   for $j=1,2,..|L_i|$ do
4.     生成由频繁项集$L_{ij}$中元素组成的1-项候选集：$HL$
5.     令剪枝的规则后件H的集合：$prunedHL=\varnothing$
6.     for $H$ $in$ $HL$ do
7.       计算可信度：$conf(P\to H)=support(L_{ij})/support(L_{ij}-H)$
8.       if $conf(P\to H)\ge minConf$ then
9.         $P\to H$规则并入规则集：$R\bigcup \{(P,H,conf(P\to H))\}$
10.         规则后件H并入剪枝的集合：$prunedHL\bigcup \{H\}$
11.       end if
12.     end for
13.     repeat
14.       利用apriori中生成候选项集的方法，合并剪枝了的k-1-项（k为项的长度）集合prunedHL，得到合并后的k-项集合HL
15.       执行步骤5-12，计算合并后的HL的可信度，并生成新的剪枝后的k项集合prunedHL
16.     until $|L_{ij}|\le k+1$ 或者 $|prunedHL|\le 1$
17.   end for
18. end for
19. 输出： 规则集$R$

---

编程实现

  数据集使用的上述杂货店的交易记录，发现频繁项集和挖掘关联规则的具体实现代码如下：

#创建数据集
def loadDataSet():
    return [['啤酒'],['面包','啤酒'],['尿布','啤酒'],['尿布','啤酒','可乐'],['牛奶','尿布','啤酒'],['面包','牛奶','可乐']]

#创建候选项集列表C1
def createC1(dataSet):
    C1=[]
    for transaction in dataSet: 
        for item in transaction:
            if not [item] in C1:
                C1.append([item])  #遍历数据集，生成只有单个商品的候选项集列表
    C1.sort()
    return list(map(frozenset,C1)) #对C1中每个项设置为一个不变的集合

#生成频繁项集，频繁项集对应的支持度
def scanDataSet(dataSet, Ck, minSupport): # 输入数据集，候选项集列表，最小支持度
    supportCnt = {}    #支持度计数
    for transaction in dataSet:
        for can in Ck:
            if can.issubset(transaction):  # 候选项集是否都包含于一条交易记录中
                if not can in supportCnt: supportCnt[can]=1
                else: supportCnt[can]+=1
    N = float(len(dataSet))  # 总记录数
    frqL = []                #频繁项集列表
    supportData = {}         #支持度字典
    for key in supportCnt:
        support = supportCnt[key]/N   #计算所有项集的支持度
        if support >= minSupport:
            frqL.insert(0,key)
            supportData[key] = support
    return frqL, supportData
#根据k-1项的频繁项集列表与项集元素个数k，生成候选项集Ck
def aprioriGen(lastLk, k): 
    Ck = []
    lenLastLk = len(lastLk)
    for i in range(lenLastLk):
        for j in range(i+1, lenLastLk):
            L1 = list(lastLk[i]); L2 = list(lastLk[j])
            L1.sort();L2.sort();
            if L1[:k-2] == L2[:k-2]:  # 如果前k-2个项相同，将两个集合合并
                Ck.append(lastLk[i] | lastLk[j])  # |为集合的并集
    return Ck

#apriori算法
def apriori(dataSet, minSupport = 0.5):
    C1 = createC1(dataSet)              #项数为1的候选集
    dataList = list(map(set, dataSet))  #对每条交易记录里的商品去重
    frqL1, supportData = scanDataSet(dataList, C1, minSupport)  #项数为1的频繁项集及其支持度
    frqL = [frqL1]     #项数为1的频繁项集添加到频繁项集列表
    k = 2           #项数k为2
    while (len(frqL[k - 2]) > 0):
        Ck = aprioriGen(frqL[k-2], k)     #基于上一频繁集列表生成新候选项集Ck
        frqLk, supportK = scanDataSet(dataList, Ck, minSupport)  #项数为k的频繁项集及其支持度
        supportData.update(supportK)  #把k项频繁项集的支持度更新到支持度字典里
        frqL.append(frqLk)   #添加k项频繁项集
        k += 1
    return frqL, supportData

#从频繁集中挖掘规则
def generateRules(frqL, supportData, minConf):
    ruleList = []   #包含可信度的规则列表
    for i in range(1, len(frqL)): #频繁项集中至少两个元素
        for freqSet in frqL[i]:
            HL1 = [frozenset([item]) for item in freqSet] #频繁项集的元素列表
            NHL1 = calcConf(freqSet, HL1, supportData, ruleList, minConf) # 计算H为单个元素时的规则P->H可信度
            mergeH(freqSet, NHL1, supportData, ruleList, minConf) # P->H1与P->H2都可信，那么尝试计算P->{H1,H2}可信度
    return ruleList

#计算可信度：P->H，返回满足可信度的H集合
def calcConf(freqSet, HL, supportData, ruleList, minConf):
    prunedH = []  #基于可信度剪枝的集合
    for H in HL:
        conf = supportData[freqSet]/supportData[freqSet-H]  # 可信度(P->H)=支持度(频繁集)/支持度(频繁集-子集H)
        if conf >= minConf:
            print(freqSet-H,'-->',H,'conf:',conf)
            ruleList.append((freqSet-H, H, conf))  # P->H可信度加入规则列表
            prunedH.append(H)
    return prunedH

#递归的合并H，计算新规则的可信度
def mergeH(freqSet, HL, supportData, ruleList, minConf):
    m = len(HL[0])   # H的元素个数
    if (len(freqSet) > (m+1)): #频繁项集比规则后件H的元素数多1个以上，就可以进一步合并
        MHL = aprioriGen(HL, m+1) #合并后H列表，H元素数+1 
        newHL = calcConf(freqSet, MHL, supportData, ruleList, minConf) #计算可信度,生成满足可信度的H列表
        if (len(newHL) > 1):  #有多于1个H，就尝试进一步合并
            mergeH(freqSet, newHL, supportData, ruleList, minConf)
#创建数据集
dataSet = loadDataSet()
#生成频繁项集及其对应的支持度
frqL,suppData=apriori(dataSet,0.3)
#生成关联规则
rules = generateRules(frqL, suppData, 0.7)

程序执行的结果如下，只得到了一条{尿布}$\to${啤酒}的强关联规则。

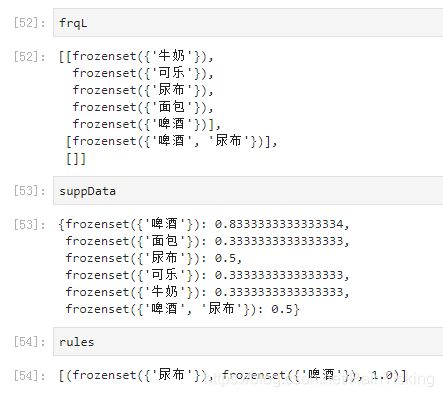
小结

  关联分析可以在大规模数据集中发现物品间有趣的关系，可以采用两种方式量化这种关系。第一种方式是使用频繁项集，它给出了一些经常在一起出现的物品；第二种方式是关联规则，它表示一种物品出现后，另一种物品极有可能也会出现。
  发现物品间不同的组合是个十分耗时的任务，不可避免的需要大量的计算资源，这就需要更加智能的方法在合理的时间范围内找到频繁项集。能够实现这一目标的一个方法是Apriori算法，它开创性的使用了基于支持度的剪枝技术，可以极大的减少检索集合的数目。Apriori原理是说如果一个元素项是不频繁的，那么包含该元素的超集也是不频繁的。Apriori算法从单元素项集开始，通过组合满足最小支持度要求的项集来形成更大的集合。
  关联分析中用到的两个度量是很有意义的。支持度可以过滤掉没有分析意义的项集，因为支持度低，意味着顾客同时购买这些商品的次数少，从商家的角度来看，并不具有分析的价值。而可信度代表着规则的强度，可信度越高，就表示一个物品在包含另一个物品的记录中出现的可能性越大，规则就越可靠，商家基于此规则制定策略，可以产出更大价值。