Floyd算法图解，C++实现Floyd算法

Floyd算法简介

Floyd算法是一种多源最短路径算法，是利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
时间复杂度：O（n^3）。
空间复杂度：O（n^2）。

以另一篇Dijkstra算法的地图为例：https://blog.csdn.net/weixin_40355471/article/details/130655729?spm=1001.2014.3001.5502

数据结构抽象

Floyd是多源最短路径算法，一次计算可以算出所有顶点到其他任意顶点的最短路径，本例计算图1景点地图的最短路径。

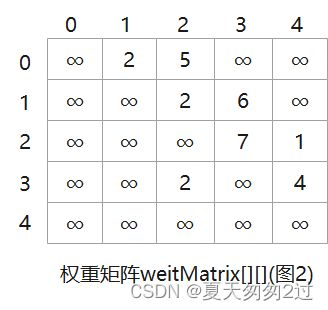
初始化权重矩阵weitMatrix[][]，如果从顶点 i 到顶点 j 有边，则weitMatrix[i][j] == 的权值，否则weitMatrix[i][j] == (无穷大)，如图2。

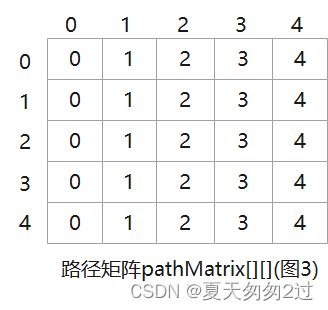
初始化路径矩阵pathMatrix[][]，初值为各个边的终点顶点的下标，如图3。

开始计算

初始状态
权重矩阵weitMatrix[][]如图2，初始两个点之间有边，则这两个点之间是连通的，如果没有边直接相连则是不通的。

Floyd算法的核心思想
选取任意一个点k，以k作为桥梁，寻找其他任意两个点i和j之间的更短路径，找到则更新权重矩阵和路径矩阵。

选取任意一个点

选取顶点1，以1作为中继，计算其他任意两点之间有没有更短路径。
借助顶点1，多了如下几条路径：
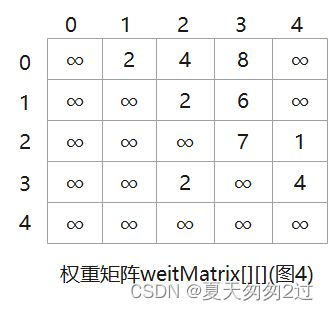
0->1->3（借道权重2+6 < 原权重∞，可以借道）
0->1->2（借道权重2+2 < 原权重5，可以借道）

一条条分析，借道权重 < 原权重时，更新权重矩阵和路径矩阵。
更新后的权重矩阵：

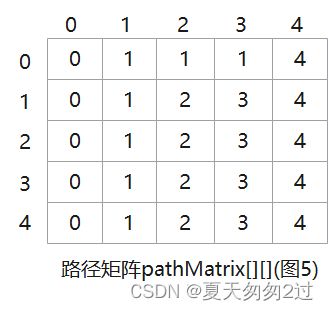
更新后的路径矩阵：

遍历所有点

重复上一步骤，直到遍历了所有顶点，得到最终的权重矩阵和路径矩阵。
最终的权重矩阵：

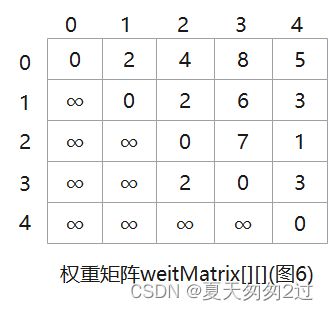
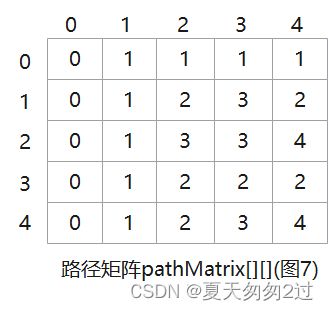
最终的路径矩阵：

计算最短路径

使用最终的权重矩阵和路径矩阵，如图6和图7，可计算任意两个顶点之间的最短路径。
示例：计算从顶点0到顶点4的最短路径：

1、先看权重矩阵，如果weitMatrix[0][4] = ∞，则表示没有路径可选，此路不通；否则表示有路径。
2、weitMatrix[0][4] = 5，表示有路径，且路径权重之和等于5。
3、看路径矩阵pathMatrix[0][4] = 1，表示从顶点1借道。
4、再看1->4，pathMatrix[1][4] = 2，表示从顶点2借道。
5、再看2->4，pathMatrix[2][4] = 4，说明从顶点可直接到终点4，得到完整的最短路径：0–>1–>2–>4。
6、其他任意两个顶点之间的最短路径均可以用这种方法计算。

C++实现Floyd算法

头文件

#ifndef FLOYD_H
#define FLOYD_H


#include
#include
#include
using namespace std;

#define MAX_WEIGHT 999//表示无穷
#define MAX_VERNUM 20//最大结点数

class Floyd//Adjacency Matrix Graph有向图，用邻接矩阵表示
{
public:
    Floyd(){};
public:
    void Create_graph();//创建图
    void Floyd_algo();//Floyd算法
    void print_path();//打印路径
    void ShowMatrix(int matrix[MAX_VERNUM][MAX_VERNUM]);//打印矩阵
private:
    int Vertexs[MAX_VERNUM];//顶点数组
    int weitMatrix[MAX_VERNUM][MAX_VERNUM];//权重矩阵
    int pathMatrix[MAX_VERNUM][MAX_VERNUM];//路径矩阵
    int VertexNum;//顶点数
    int EdgeNum;//边数
};

#endif // FLOYD_H

源文件

#include "Floyd.h"

int g_VertexNum = 5;
int g_EdgeNum = 8;
int g_edges[8][3] = {//边的集合
    //起点，终点，权值
    {0, 1, 2},
    {0, 2, 5},
    {1, 2, 2},
    {1, 3, 6},
    {2, 3, 7},
    {2, 4, 1},
    {3, 2, 2},
    {3, 4, 4}
};

void Floyd::Create_graph()
{
    VertexNum = g_VertexNum;
    EdgeNum   = g_EdgeNum;
    //初始化顶点数组
    for (int i = 0; i < VertexNum; i++)
    {
        Vertexs[i] = i;
    }

    //初始化邻接矩阵，权重初始化为无穷大
    for (int i = 0; i < VertexNum; i++)
    {
        for (int j = 0; j < VertexNum; j++)
        {
            weitMatrix[i][j] = MAX_WEIGHT;
        }
    }

    //权重矩阵赋值
    for (int i = 0; i < EdgeNum; i++)
    {
        weitMatrix[g_edges[i][0]][g_edges[i][1]] = g_edges[i][2];
    }

    //初始化路径矩阵，初值为各个边的终点顶点的下标
    for (int i = 0; i < VertexNum; i++)
    {
        for (int j = 0; j < VertexNum; j++)
        {
            pathMatrix[i][j] = j;
        }
    }

    cout << "init weight matrix:" << endl;
    ShowMatrix(weitMatrix);

    cout << "init pathMatrix:" << endl;
    ShowMatrix(pathMatrix);

    return;
}

void Floyd::Floyd_algo()
{
    for (int k = 0; k < VertexNum; k++)
        for (int i = 0; i < VertexNum; i++)
            for (int j = 0; j < VertexNum; j++)
                //以k做为桥梁，寻找ij之间的更短路径，找到则更新
                if (weitMatrix[i][k] + weitMatrix[k][j] < weitMatrix[i][j])
                {
                    weitMatrix[i][j] = weitMatrix[i][k] + weitMatrix[k][j];//更新i->j路径权重和
                    pathMatrix[i][j] = pathMatrix[i][k];//i->j，经过k路径更短，先到k
                }

    //更改到自身距离为0
    for (int i = 0; i < VertexNum; i++)
        for (int j = 0; j < VertexNum; j++)
            if (i == j)
                weitMatrix[i][j] = 0;

    cout << "Floyd algo:" << endl;

    cout << "weight matrix:" << endl;
    ShowMatrix(weitMatrix);//打印权重矩阵

    cout << "path matrix:" << endl;
    ShowMatrix(pathMatrix);//打印路径矩阵
}

void Floyd::print_path()
{
    cout << "The shortest path between any two vertices:" << endl;
    int row = 0;
    int col = 0;
    int temp = 0;
    for (row = 0; row < VertexNum; row++)
    {
        for (col = 0; col < VertexNum; col++)
        {
            if(row == col)//忽略自己到自己
                continue;
            if (weitMatrix[row][col] != MAX_WEIGHT)
            {
                cout << "v" << to_string(row) << "---" << "v" << to_string(col) << " weight: " << weitMatrix[row][col] << " path: " << " v" << to_string(row);
                temp = pathMatrix[row][col];
                //循环输出途径的每条路径，直到终点。
                while (temp != col)
                {
                    cout << "-->" << "v" << to_string(temp);
                    temp = pathMatrix[temp][col];
                }
                cout << "-->" << "v" << to_string(col) << endl;
            }
        }
        cout << endl;
    }
}

void Floyd::ShowMatrix(int matrix[MAX_VERNUM][MAX_VERNUM])
{
    for (int i = 0; i < VertexNum; i++)
    {
        for (int j = 0; j < VertexNum; j++)
        {
            cout << setw(4) << matrix[i][j] << " ";
        }
        cout << endl;
    }
}

调用方法：

Floyd mFloyd;
mFloyd.Create_graph();
mFloyd.Floyd_algo();
mFloyd.print_path();

打印输出：

init weight matrix:
 999    2    5  999  999 
 999  999    2    6  999 
 999  999  999    7    1 
 999  999    2  999    4 
 999  999  999  999  999 
init pathMatrix:
   0    1    2    3    4 
   0    1    2    3    4 
   0    1    2    3    4 
   0    1    2    3    4 
   0    1    2    3    4 
Floyd algo:
weight matrix:
   0    2    4    8    5 
 999    0    2    6    3 
 999  999    0    7    1 
 999  999    2    0    3 
 999  999  999  999    0 
path matrix:
   0    1    1    1    1 
   0    1    2    3    2 
   0    1    3    3    4 
   0    1    2    2    2 
   0    1    2    3    4 

最短路径：

The shortest path between any two vertices:
v0---v1 weight: 2 path:  v0-->v1
v0---v2 weight: 4 path:  v0-->v1-->v2
v0---v3 weight: 8 path:  v0-->v1-->v3
v0---v4 weight: 5 path:  v0-->v1-->v2-->v4

v1---v2 weight: 2 path:  v1-->v2
v1---v3 weight: 6 path:  v1-->v3
v1---v4 weight: 3 path:  v1-->v2-->v4

v2---v3 weight: 7 path:  v2-->v3
v2---v4 weight: 1 path:  v2-->v4

v3---v2 weight: 2 path:  v3-->v2
v3---v4 weight: 3 path:  v3-->v2-->v4