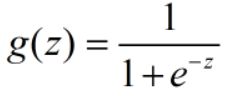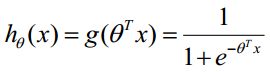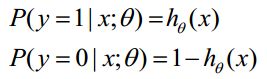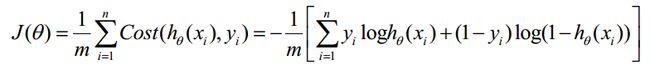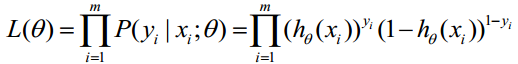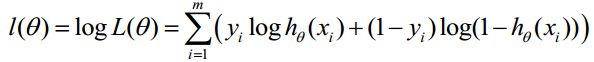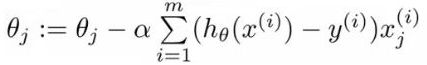逻辑回归（Logistic Regression）

1. 逻辑回归简介

逻辑回归（Logistic Regression）虽然被称为回归，但其实际上是分类模型，并常用于二分类。逻辑回归与线性回归本质上是类似的，相较线性回归只是多了一个Logistic函数（或称为Sigmoid函数）。

1.1 分类和回归

分类和回归是机器学习可以解决的两大主要问题，从预测值的类型上看，连续变量预测的定量输出称为回归；离散变量预测的定性输出称为分类。例如：预测明天多少度，是一个回归任务；预测明天阴还是晴，就是一个分类任务。

1.2 逻辑回归

Logistic Regression原理与Linear Regression回归类似，其主要流程如下：
（1）构建预测函数。一般来说在构建之前，需要根据数据来确定函数模型，是线性还是非线性。
（2）构建Cost函数(损失函数)。该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差。
（3）采用梯度下降算法，minJ(θ)。在数据量很大时，梯度下降算法执行起来会较慢。因此出现了随机梯度下降等算法进行优化。

2. 逻辑回归原理

2.1 构造预测函数

在线性回归中模型中预测函数为：

逻辑回归作为分类问题，结果h = {1 or 0}即可。若逻辑回归采用线性回归预测函数则会产生远大于1或远小于0得值，不便于预测。因此线性回归预测函数需要做一定改进。设想如果有一个函数h(x)能够把预测结果值压缩到0-1这个区间，那么我们就可以设定一个阈值s，若h(x) >= s,则认定为预测结果为1，否之为0。

实际中也存在这样的函数：Logistic函数（或称为Sigmoid函数），函数表达式为：

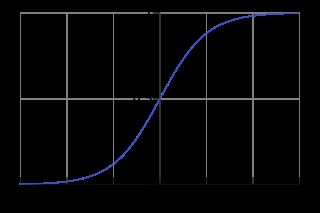
其图像如下图所示：

对于线性边界的情况，边界形式如下：

构造预测函数为：

函数h_θ(x)的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为如下公式所示，暂将其命名为公式 （1）：

2.2 构造损失函数 J

Cost函数和J函数如下，它们是基于最大似然估计推导得到的：

下面详细说明推导的过程：

2.1节公式(1) 综合起来可以写成：

取似然函数为：

对数似然函数为：

最大似然估计就是求使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。但是，在Andrew Ng的课程中将取为下式，即：

2.3 梯度下降法求J(θ)的最小值

θ更新过程如下：

经化简后θ的最终更新过程可以写成：

另外，可以通过向量化，即使用矩阵计算来代替for循环，以简化计算过程，提高效率；可以通过正则化解决过拟合问题（过拟合即过分拟合了训练数据，使得模型的复杂度提高，泛化能力较差（对未知数据的预测能力））。

3. 逻辑回归特点

优点：
（1）简单实现，模型的可解释性很好。
（2）训练速度快。计算的量只和特征的数目有关，不需要缩放输入特征等等。
（3）资源占用小。因为只需要存储各个维度的特征值。

缺点：
（1）准确率不是很高，就是因为模型（非常类似线性模型），很难拟合数据的真实分布，容易导致过拟合。
（2）难处理数据不平衡的问题。
（3）逻辑回归本身无法解决非线性问题，因为它的决策边界是线性的。
（4）高度依赖正确的数据表示。

4. 逻辑回归的应用场景

当Y变量只有两个值时，当面临分类问题时，可以考虑使用逻辑回归。

逻辑回归也用于多分类别分类。有很多种多分类算法，如随机森林分类器或者朴素贝叶斯分类器等等。逻辑回归也可以用于多分类任务。可以通过一些技巧，分两种策略：

一对多策略：基本思想是将第i种类型的所有样本作为正例，将剩下的所有样本作为负例。进行训练得出一个分类器。这样，我们就得到N个分类器。预测的时候，将样本给N个分类器，获得N个结果，选择其中概率值最大的那个作为结果。

一对一策略：这种策略，假设有N个类别，不同的类别之间，训练一个分类器，训练得到的结果有$C_N^2$种不同的分类器。预测的时候，将样本给所有的分类器，会有N(N-1)个结果，最终结果通过“投票”产生。

5. 逻辑回归的Python应用

5.1 自定义函数实现逻辑回归

可以自定义sigmod函数、损失函数、梯度下降等实现逻辑回归，如下代码所示：

import numpy as np
import matplotlib.pyplot as plt
 
 
# sigmod函数，即得分函数,计算数据的概率是0还是1；得到y大于等于0.5是1，y小于等于0.5为0。
def sigmod(x):
    return 1 / (1 + np.exp(-x))
 
# 损失函数
# hx是概率估计值，是sigmod(x)得来的值，y是样本真值
def cost(hx, y):
    return -y * np.log(hx) - (1 - y) * np.log(1 - hx)
 
# 梯度下降
def gradient(current_para, x, y, learning_rate):
    m = len(y)
    matrix_gradient = np.zeros(len(x[0]))
    for i in range(m):
        current_x = x[i]
        current_y = y[i]
        current_x = np.asarray(current_x)
        matrix_gradient += (sigmod(np.dot(current_para, current_x)) - current_y) * current_x
    new_para = current_para - learning_rate * matrix_gradient
    return new_para
 
# 误差计算
def error(para, x, y):
    total = len(y)
    error_num = 0
    for i in range(total):
        current_x = x[i]
        current_y = y[i]
        hx = sigmod(np.dot(para, current_x))  # LR算法
        if cost(hx, current_y) > 0.5:  # 进一步计算损失
            error_num += 1
    return error_num / total
 
# 训练
def train(initial_para, x, y, learning_rate, num_iter):
    dataMat = np.asarray(x)
    labelMat = np.asarray(y)
    para = initial_para
    for i in range(num_iter + 1):
        para = gradient(para, dataMat, labelMat, learning_rate)  # 梯度下降法
        if i % 100 == 0:
            err = error(para, dataMat, labelMat)
            print("iter:" + str(i) + " ; error:" + str(err))
    return para
 
# 数据集加载
def load_dataset():
    dataMat = []
    labelMat = []
    with open("logistic_regression_binary.csv", "r+") as file_object:
        lines = file_object.readlines()
        for line in lines:
            line_array = line.strip().split()
            dataMat.append([1.0, float(line_array[0]), float(line_array[1])])  # 数据
            labelMat.append(int(line_array[2]))  # 标签
    return dataMat, labelMat
 
# 绘制图形
def plotBestFit(wei, data, label):
    if type(wei).__name__ == 'ndarray':
        weights = wei
    else:
        weights = wei.getA()
    fig = plt.figure(0)
    ax = fig.add_subplot(111)
    xxx = np.arange(-3, 3, 0.1)
    yyy = - weights[0] / weights[2] - weights[1] / weights[2] * xxx
    ax.plot(xxx, yyy)
    cord1 = []
    cord0 = []
    for i in range(len(label)):
        if label[i] == 1:
            cord1.append(data[i][1:3])
        else:
            cord0.append(data[i][1:3])
    cord1 = np.array(cord1)
    cord0 = np.array(cord0)
    ax.scatter(cord1[:, 0], cord1[:, 1], c='g')
    ax.scatter(cord0[:, 0], cord0[:, 1], c='r')
    plt.show()
 
def logistic_regression():
    x, y = load_dataset()
    n = len(x[0])
    initial_para = np.ones(n)
    learning_rate = 0.001
    num_iter = 1000
    print("初始参数：", initial_para)
    para = train(initial_para, x, y, learning_rate, num_iter)
    print("训练所得参数：", para)
    plotBestFit(para, x, y)
 
    
if __name__=="__main__":
    logistic_regression()

5.2 sklearn库LogisticRegression函数的应用

另外，可以通过sklearn库的逻辑回归函数来训练模型并预测，其函数原型如下：

LogisticRegression(C=1.0,class_weight=None,dual=False,fit_intercept=True,intercept_scaling=1,max_iter=100,multi_class='ovr',n_jobs=1,penalty='l2',random_state=None,solver='liblinear',tol=0.0001,verbose=0,warm_start=False)

参数说明:

C：正则化系数λ的倒数，默认为1.0。

class_weight：用于标示分类模型中各种类型的权重，不考虑权重，即为None。

dual：对偶或原始方法，bool类型，默认为False。

fit_intercept：是否存在截距或偏差，bool类型，默认为True。

intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用，float类型，默认为1。

max_iter：算法收敛最大迭代次数，int类型，默认为10，仅在正则化优化算法为newton-cg, sag和lbfgs才有用。

multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。

n_jobs：并行数，int类型，默认为1。

penalty：用于指定惩罚项中使用的规范，str类型，可选参数为l1和l2，默认为l2。

random_state：随机数种子，int类型，可选参数，默认为无。

solver：优化算法选择参数，决定了我们对逻辑回归损失函数的优化方法。有五个可选参数，即newtoncg,lbfgs,liblinear,sag,saga。对于小型数据集来说，‘liblinear’是一个不错的选择，而‘sag’和‘saga’对于大型数据集则更快。

tol：停止求解的标准，float类型，默认为1e-4。

verbose：日志冗长度，int类型，默认为0。

warm_start：热启动参数，bool类型，默认为False。

下面以通过泰坦尼克号数据集预测乘客生还情况为例，说明上述函数的使用：

from sklearn.model_selection import train_test_split
# 建立模型用的训练数据集和验证数据集
train_X, test_X, train_y, test_y = train_test_split(source_X , source_y, train_size=.8)

# 导入算法
from sklearn.linear_model import LogisticRegression
# 创建模型：逻辑回归（logisic regression）
model = LogisticRegression()
# 训练模型
model.fit( train_X , train_y )
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)

# 评估模型
# 分类问题，score得到的是模型的正确率
model.score(test_X , test_y )
# k折交叉验证
from sklearn import model_selection
# 将训练集分成5份，4份用来训练模型，1份用来预测，这样就可以用不同的训练集在一个模型中训练
print(model_selection.cross_val_score(model, source_X, source_y, cv=5))

# 结果预测
pred_Y = model.predict(pred_X)
# 生成的预测值是浮点数（0.0,1,0）,所以要对数据类型进行转换
pred_Y=pred_Y.astype(int)
# 乘客id
passenger_id = full.loc[sourceRow:,'PassengerId']
# 数据框：乘客id，预测生存情况的值
predDf = pd.DataFrame(
    { 'PassengerId': passenger_id ,
     'Survived': pred_Y } )
predDf.shape
print(predDf.head())
# 保存结果
predDf.to_csv('titanic_pred.csv', index = False )

6. 源码仓库地址

图像处理、机器学习的常用算法汇总